2016中国大学生程序设计竞赛 - 女生专场
【VJ地址】:https://cn.vjudge.net/contest/180373#problem/A
【题意】:t个样例,n个气球,给出颜色和该颜色气球的数量,按照数量多少降序排列。
【分析】:结构体排序,水题。
【代码】:

#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<string> #include<vector> #include<stack> #include<bitset> #include<cstdlib> #include<cmath> #include<set> #include<list> #include<deque> #include<map> #include<queue> #define ll long long #define inf 0x3fffffff const int maxn=1005; using namespace std; struct node { char s[20]; int num; }a[maxn]; bool cmp(node a,node b) { return a.num>b.num; } int main() { int t; int n; scanf("%d",&t); while(t--) { scanf("%d",&n); for(int i=0;i<n;i++) { scanf("%s%d",a[i].s,&a[i].num); } sort(a,a+n,cmp); for(int i=0;i<n;i++) printf("%s%c",a[i].s,i==n-1?'\n':' '); } return 0; }
【题意】:给你一个数字n,求它的拆分方式的种数的二进制表达值。比如3,拆分方式有4种,1/1/1+1/2+2/1+3 ,故4的二进制表达为100。
【分析】:找规律 / 排列组合-隔板法 ,水题。首先拆分方式的种数可以找出规律=2^(n-1)。而2^n次方化为二进制又是一个规律,即首项总为1,后面总为0 ,0的个数为n个,比如2^3二进制为1000,1后面接了n=3个0,。
【代码】:

#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<string> #include<vector> #include<stack> #include<bitset> #include<cstdlib> #include<cmath> #include<set> #include<list> #include<deque> #include<map> #include<queue> #define ll long long #define inf 0x3fffffff const int maxn=1005; using namespace std; int main() { int t; int n; scanf("%d",&t); while(t--) { scanf("%d",&n); printf("1"); n--; for(int i=0;i<n;i++) printf("0"); printf("\n"); } return 0; }
【题意】:n个人(2-200)参加游戏,每个人选择1-100之间的数。然后得到所有数的平均数,再*=2/3,设得到的数为m。如果一个人选的数比m小且距离m最近,那么其便在所有选数相同的人中等概率中奖。现在其他n-1个人选择的数已经确定了,问你选什么数拥有最高中奖率。
【分析】:数学公式推导。设x为所求数,((sum+x)/n)*(2/3)=x ——> x=*sum/(3*n-2)。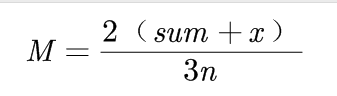
【代码】:

#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<string> #include<vector> #include<stack> #include<bitset> #include<cstdlib> #include<cmath> #include<set> #include<list> #include<deque> #include<map> #include<queue> #define ll long long #define inf 0x3fffffff const int maxn=115; using namespace std; int main() { int t,n,sum; char a[maxn]; scanf("%d",&t); while(t--) { sum=0; scanf("%d",&n); for(int i=0;i<n-1;i++) { scanf("%d",&a[i]); sum+=a[i]; } int x=2*sum/(3*n-2); sum=1; for(int i=0;i<n-1;i++) { if(a[i]==x) sum++; } printf("%d %.2lf\n",x,1.0/sum); } return 0; }
D HDU - 5705 (预备知识: https://wenku.baidu.com/view/778af7706294dd88d0d26bf1.html http://res.tongyi.com/resources/old_article/student/846.html http://blog.csdn.net/u014082714/article/details/43086965)
【题意】:时间为12小时制,告诉你一个时刻,输出在这个时刻之后的下一个时刻,满足该时刻时针分针恰好相差某个角度a,满足要求的时刻不一定恰好以秒为单位,可以是秒与秒之间的时刻,向下取整。
【分析】:追及问题,时间转换,细节。
一个计算角度的公式:二分之十一乘Y减三十乘X ,算出来的结果取绝对值。如果结果超出一百八十度,用360度去减。Y是分针,X是时针。

怎样时针分针才能相差某个角度呢?钟表有360个度,
1.考虑时针位置
每小时30°,每分钟1/2°,每秒钟1/120°,不妨使所有与角度相关的单位都*=120,转化成整数,避免误差——> 以秒为基本单位
转变为
每小时3600°,每分钟60°,每秒1°
2.考虑分针位置
每分钟6°,每秒钟0.1°
我们*=120
变为每分钟720°,每秒钟12°
首先先将当前时针和分针的位置确定,为了确保满足时针和分针夹角为a的情况不是当前时间 ,我们先将时间往后拨1秒,即分针走12°,时针走1°
1.分针追上时针的夹角为θ>=180°,夹角a<360°-θ
那么时针和分针达到a的时间为(θ-a*120)/11°
2.分针追上时针的夹角为θ>=180°,夹角a≥360°-θ
那么时针和分针达到a的时间为(θ-(360°-a)*120)/11°
3.分针追上时针的夹角为θ<180°,夹角a<=θ
那么时针和分针达到a的时间为(d-a*120)/11°
4.分针追上时针的夹角为θ<180°,夹角a>θ
那么时针和分针达到a的时间为(d+a*120)/11°
【代码】:

#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<string> #include<vector> #include<stack> #include<bitset> #include<cstdlib> #include<cmath> #include<set> #include<list> #include<deque> #include<map> #include<queue> #define ll long long const int maxn=115; #define exp 1e-10 #define bitnum(a) __builtin_popcount(a) using namespace std; const int N = 100005; const int M = 120; const int inf = 1600000000; const int mod = 2009; int solve(int u,int v,int a) { int d,ans; d=(v+M*360-u)%(M*360); if(d>=M*180) { if(a*M<360*M-d) ans=v+(d-a*M)/11; else ans=v+(d-(360-a)*M)/11; } else { if(a*M<=d) ans=v+(d-a*M)/11; else ans=v+(d+a*M)/11; } return ans; } int main() { int h,m,s,a,u,v,p=1,ss,mm,hh,ans; while(~scanf("%d:%d:%d%d",&h,&m,&s,&a)) { u=(12*(m*60+s+1))%(M*360); v=h*3600+m*60+s+1; ans=solve(u,v,a); hh=ans/3600%12; mm=ans/60%60; ss=ans%60; printf("Case #%d: %02d:%02d:%02d\n",p++,hh,mm,ss); } return 0; }
【题意】:在二维字符矩阵分别找“girl”和‘’cat‘’的个数。
【分析】:DFS。使用DFS,先在数组中搜索单词中第一个字符,再以此字符为起点进行 DFS 搜索,搜索方向为前后左右四个方向。在递归是注意标注当前访问的矩阵字符。若搜索出的路径与单词 一致,则在网格中存在此单词。(要注意的一点是把所需要匹配的字符串用数组存储起来,然后在DFS的过程中不断更新下一步所要匹配的字母即可。
【代码】:

#include <iostream> #include <cstdio> using namespace std; char Map[1010][1010]; char ans[2][10]= {{"cat"},{"girl"}}; int dir[4][2]= {0,1,0,-1,1,0,-1,0}; //4行2列 int n,m,s1,s2; void dfs(int x,int y,int flag,int num)//flag用来标记我当前找的字符串是cat还是girl,num用来表示当前找到了是第几个字符。 { if (flag==1)//girl { if (num==3)//找到了girl的长度就加加 { s1++; return; } for (int i=0; i<4; i++) { int X=x+dir[i][0]; int Y=y+dir[i][1]; if (X>=0&&X<n&&Y>=0&&Y<m&&(Map[X][Y]==ans[flag][num+1]))//一个字符一个字符比较,看是否为我接下去要找的那个字符 { dfs(X,Y,1,num+1); } } } if (flag==0) { if (num==2) { s2++; return; } for (int i=0; i<4; i++) { int X=x+dir[i][0]; int Y=y+dir[i][1]; if (X>=0&&X<n&&Y>=0&&Y<m&&(Map[X][Y]==ans[flag][num+1])) { dfs(X,Y,0,num+1); } } } } int main() { int t; scanf("%d",&t); while (t--) { s1=s2=0; scanf("%d%d",&n,&m); for (int i=0; i<n; i++) { scanf("%s",Map[i]); } for (int i=0; i<n; i++) { for (int j=0; j<m; j++) { if (Map[i][j]=='g') dfs(i,j,1,0); if (Map[i][j]=='c') dfs(i,j,0,0); } } printf ("%d %d\n",s1,s2); } return 0; }
【题意】:给定a,b,c三个串,问c能否按序分成a和b串,不要求连续。
【分析】:字符串处理/动态规划。
动态规划:
http://blog.csdn.net/druning/article/details/51823197
http://www.cnblogs.com/Ash-ly/p/5877070.html
题目链接:
http://poj.org/problem?id=2192
http://acm.split.hdu.edu.cn/showproblem.php?pid=5707
http://acm.split.hdu.edu.cn/showproblem.php?pid=1501
这三道题除了输入输出格式不一样,其他都一样,意思是给你三个字符串,问你能不能由前两个组成第三个,要按顺序;
f[i][j] 表示第一个字符串用了前i个位置(第i个位置已匹配),第二个字符串的前j个位置(第j个位置已匹配)
是否可以对c串成功匹配(成功匹配则必然会匹配到c串的前i+j个位置)。
f[i][j] ==1则表示可以成功匹配
f[i][j] ==0则表示无法成功匹配
【代码】:

#include<stdio.h> #include<iostream> #include<string.h> #include<algorithm> #include<map> using namespace std; map<char,int>ma,mc; int main() { string a,b,c; while(cin>>a>>b>>c) { ma.clear(); mc.clear(); int lena=a.length(); int lenb=b.length(); int lenc=c.length(); for(int i=0;i<lena;i++) { ma[a[i]]++; } for(int i=0;i<lenb;i++) { ma[b[i]]++; } int x=0,y=0; for(int i=0;i<lenc;i++) { mc[c[i]]++; if(x<lena&&c[i]==a[x]) x++; if(y<lenb&&c[i]==b[y]) y++; } map<char,int>::iterator it; int flag=1; for(it=mc.begin();it!=mc.end();it++) { if(mc[it->first]!=ma[it->first]) { flag=0; break; } } if(flag) { if(x==lena&&y==lenb) { printf("Yes\n"); } else printf("No\n"); } else printf("No\n"); } }

#include<cstdio> #include<cstring> #define F(i,a,b) for(int i=a;i<=b;i++) char a[2011],b[2011],c[2011],dp[2011][2011]; int lena,lenb,lenc; int main(){ while(~scanf("%s%s%s",a,b,c)){ lena=strlen(a),lenb=strlen(b),lenc=strlen(c); if(lena+lenb!=lenc){puts("No");continue;} memset(dp,0,sizeof(dp)),dp[0][0]=1; F(i,0,lenc-1)F(j,0,i){ if(!dp[i][j])continue; if(c[i]==a[j])dp[i+1][j+1]=1; if(c[i]==b[i-j])dp[i+1][j]=1; } if(dp[lenc][lena])puts("Yes"); else puts("No"); } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号