个人第2次作业：熟悉使用工具

Gayhub 项目地址

初始化及克隆仓库，创建项目

初始化并克隆仓库:

40184@Rongz MINGW32 ~
$ cd e:

40184@Rongz MINGW32 /e
$ cd RongGit/

40184@Rongz MINGW32 /e/RongGit
$ git init
Initialized empty Git repository in E:/RongGit/.git/

40184@Rongz MINGW32 /e/RongGit (master)
$ git clone https://github.com/Cherish599/AchaoCalculator.git
Cloning into 'AchaoCalculator'...
remote: Enumerating objects: 6, done.
remote: Counting objects: 100% (6/6), done.
remote: Compressing objects: 100% (4/4), done.
remote: Total 6 (delta 0), reused 4 (delta 0), pack-reused 0
Unpacking objects: 100% (6/6), done.

创建项目:

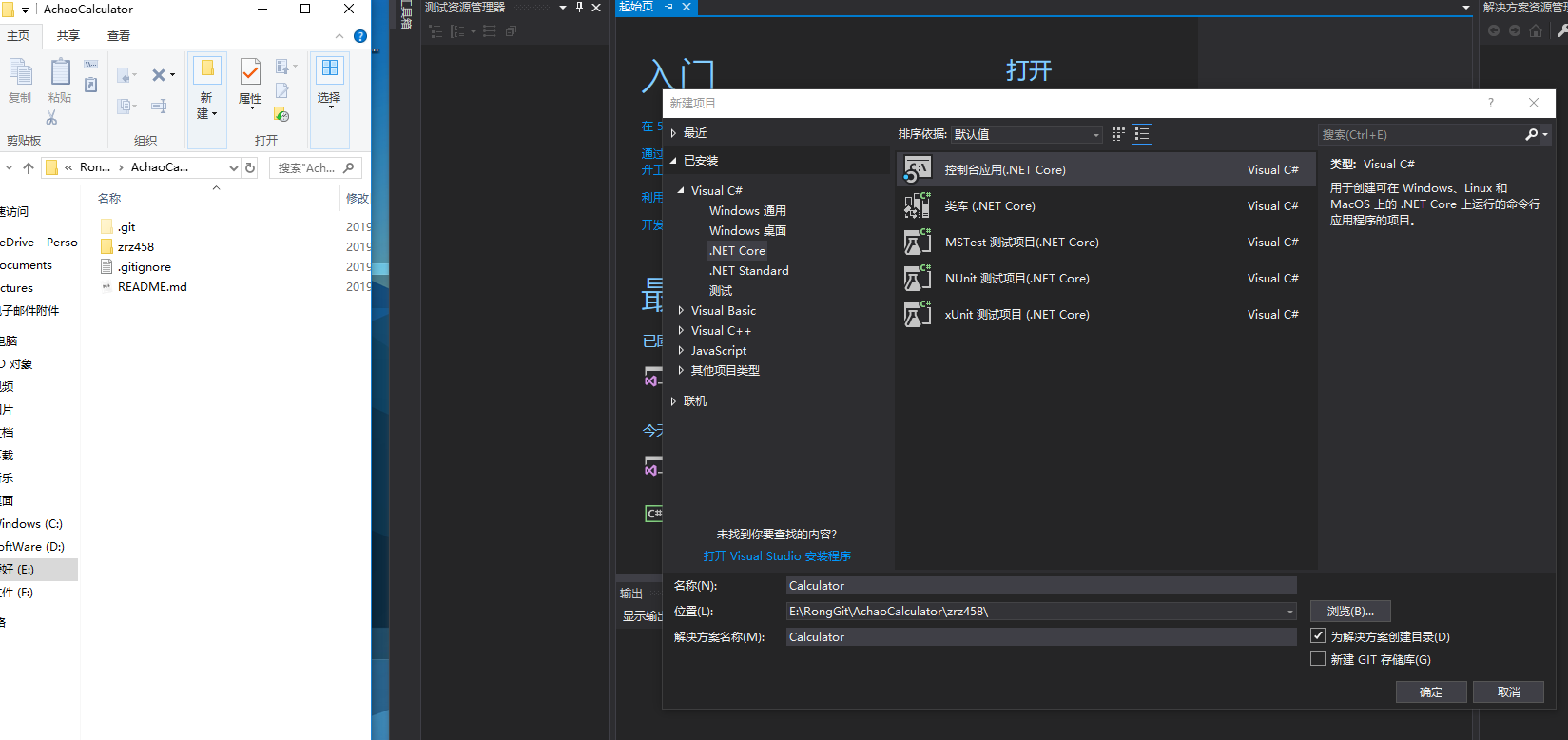
代码编写

工具类 Result：

用途封装代码执行结果

/// <summary>
/// 前缀表达式字符串
/// </summary>
internal StringBuilder infixFormula;

/// <summary>
/// 后缀表达式队列
/// </summary>
internal Queue<string> formulaQueue;

/// <summary>
/// 计算结果
/// </summary>
internal int result;

中缀表达式式生成：

解决思路：

问题化简：通过观察我们知道，每一个表达式都有三部分组成——乘除法表达式部分、加减法表达式部分、和连接二者的加减号部分。如1+2+3 * 4/2，就是1+2和 3 * 4/2及+组成。所以我们大体思路就是创建两个分别生成乘除法表达式和加减法表达式的函数，然后用加减法将他们组合起来。

1. multipleFormulaGenerator(int count)函数

   给定一个乘除法表达式所含操作数的个数，生成一个随机的乘除法表达式，并以队列的形式返回

   比如:count=3，输出可能是1 * 2 * 3

   ​ count=4，输出可能是1 * 2 * 3 / 2

   1. 解决被除数和除数整除的问题思路
      1. 先生成一个数 num ，将它放入队列
         1. 生成一个符号（* 或 /）
            1. 如果是 * ：新生成一个数 num2，并与之前 num 相乘 ，用 num 记录相乘的结果
            2. 如果是 / ：寻找一个 num 的因式作为除数
      2. 输出队列
   2. 解决寻找一个数所有因式的思路（chooseRandomFactor(int num)实现）
      1. i 从 1 遍历到 根号 num
      2. 如果 num % i==0
      3. 将 i 和 num/i 存入一个数组（存入的两个数就是num的两个因式）
      4. 随机返回数组中的一个因式，就得到了 num 的一个随机的因式

   
   /// <summary>
   /// 给定一个乘除法表达式所含操作数的个数，生成一个随机的乘除法表达式，并以队列的形式返回
   /// </summary>
   /// <param name="count"> 符号数个数 </param>
   /// <returns> 乘除法表达式队列 </returns>
   public static Queue<string> multipleFormulaGenerator(int count)
   {
       Queue<string> queue = new Queue<string>();
       int num = random.Next(maxNum) + 1;
       queue.Enqueue(num.ToString());
       while (--count > 0)
       {
           string option = op[2 + random.Next(2)];
           if (string.ReferenceEquals(option, "/"))
           {
               int factor = chooseRandomFactor(num);
               queue.Enqueue(option);
               queue.Enqueue(factor.ToString());
               num /= factor;
           }
           else
           {
               int num2 = random2.Next(maxNum) + 1;
               queue.Enqueue(option);
               queue.Enqueue(num2.ToString());
               num *= num2;
           }
       }
       return queue;
   }
   
   /// <summary>
   /// 从一个数的所有因式中随机选择一个返回
   /// </summary>
   /// <param name="num"> 数 </param>
   /// <returns> num 的一个因式 </returns>
   private static int chooseRandomFactor(int num)
   {
       int[] arr = new int[num + 1];
       int size = 0;
       for (int i = 1; i <= Math.Sqrt(num); i++)
       {
           if (num % i == 0)
           {
               arr[size++] = i;
               arr[size++] = num / i;
           }
       }
       int r = random2.Next(size);
       return arr[r];
   }
   

2. additionAndSubtractionFormulaGenerator(int count)函数

   给定一个加减法表达式所含操作数的个数，生成一个随机的加减法表达式，并以队列的形式返回

   count 含义如 multipleFormulaGenerator() 的 count

   思路简单，看代码

   
   /// <summary>
   /// 给定一个加减法表达式所含操作数的个数，生成一个随机的加减法表达式，并以队列的形式返回
   /// </summary>
   /// <param name="count"> 符号数个数 </param>
   /// <returns> 加减法表达式队列 </returns>
   public static Queue<string> additionAndSubtractionFormulaGenerator(int count)
   {
       Queue<string> queue = new Queue<string>();
       int num = random.Next(maxNum) + 1;
       queue.Enqueue(num.ToString());
       while (--count > 0)
       {
           string option = op[random.Next(2)];
           queue.Enqueue(option);
           queue.Enqueue((random.Next(maxNum) + 1).ToString());
       }
       return queue;
   }
   

3. formulaMaker()函数

   随机生成多个乘除法表达式和加减法表达式，并将他们用 + 或 - 号拼接

   /// <summary>
   /// 表达式生成器
   /// </summary>
   /// <returns> 中缀表达式队列 </returns>
   public static Result formulaMaker()
   {
       Queue<string> queue = new Queue<string>();
       StringBuilder sb = new StringBuilder();
       int maxNumCount2 = maxNumCount;
       while (maxNumCount2-- > 0)
       {
           string option = op[random.Next(2)];
           int nextBoolean = random.Next(0,1);
   
           if (nextBoolean==0)
           {
               Queue<string> queue1 = multipleFormulaGenerator(random.Next(3) + 1);
               mergeQueue(queue, queue1);
           }
           else
           {
               mergeQueue(queue, additionAndSubtractionFormulaGenerator(random2.Next(3) + 1));
           }
           if (maxNumCount2 != 0)
           {
               queue.Enqueue(op[random.Next(2)]);
           }
       }
       foreach (string s in queue)
       {
           sb.Append(s);
       }
       return new Result(sb, queue);
   }
   

4. changeToPostfix(Queue queue)函数

   将formulaMaker()生成的中缀表达式，转化为后缀表达式（4+4/2 * 3-5 * 2 --> 442/3 * +52 * - ）

   1. 如果是操作数直接输出到操作数队列
   2. 如果是操作符
      1. 操作符栈为空直接输出到操作符栈
      2. 如果不为空，循环判断如果 操作符栈顶的符号优先级大于等于当前符号，则将操作符栈的符号输出，然后再将操作数入栈。否则将操作数压栈
   3. 将操作符栈的所有元素输出

   /// <summary>
   /// 中缀表达式转后缀表达
   /// </summary>
   /// <param name="queue"> 中缀表达式队列 </param>
   /// <returns> 后缀表达式堆栈 </returns>
   public static Queue<string> changeToPostfix(Queue<string> queue)
   {
       Queue<string> queue2 = new Queue<string>(); // 保存操作数
       Stack<string> stack2 = new Stack<string>(); // 保存操作符
       while (queue.Count > 0)
       {
           string symbol = queue.Dequeue();
           if (precedence(symbol) > 0)
           { //检查symbol是否是一个操作数
               while (stack2.Count > 0 && precedence(stack2.Peek()) >= precedence(symbol))
               {
                   queue2.Enqueue(stack2.Pop());
               }
               stack2.Push(symbol);
           }
           else
           { //symbol 不是一个操作数
               queue2.Enqueue(symbol);
           }
       }
       while (stack2.Count > 0)
       {
           queue2.Enqueue(stack2.Pop());
       }
       return queue2;
   }
   

5. calculate(Queue stack)

   将 changeToPostfix()生成的后缀表达式进行计算求值

   1. 如果不是操作符直接输出到操作数栈
   2. 如果是操作符，将操作数栈栈顶的两个操作数弹出做运算，存入操作数栈
      3.最后将操作数栈顶的的元素弹出

   /// <summary>
   /// 计算函数
   /// 用于计算后缀表达式的值
   /// </summary>
   /// <param name="queue"> 后缀表达式堆栈 </param>
   /// <returns> 计算结果 </returns>
   public static int calculate(Queue<string> queue)
   {
       Stack<string> stack1 = new Stack<string>(); // 保存操作数
       Stack<string> stack2 = new Stack<string>(); // 保存操作符
       foreach (string symbol in stack)
       {
           if (!symbol.Equals("+") && !symbol.Equals("-") && !symbol.Equals("/") && !symbol.Equals("*"))
           {
               stack1.Push(symbol);
           }
           else
           {
               int a = int.Parse(stack1.Pop()), b = int.Parse(stack1.Pop());
               switch (symbol)
               {
                   case "+":
                       stack1.Push((a + b).ToString());
                       break;
                   case "-":
                       stack1.Push((b - a).ToString());
                       break;
                   case "*":
                       stack1.Push((a * b).ToString());
                       break;
                   default:
                       stack1.Push((b / a).ToString());
                       break;
               }
           }
       }
       return int.Parse(stack1.Pop());
   }
   

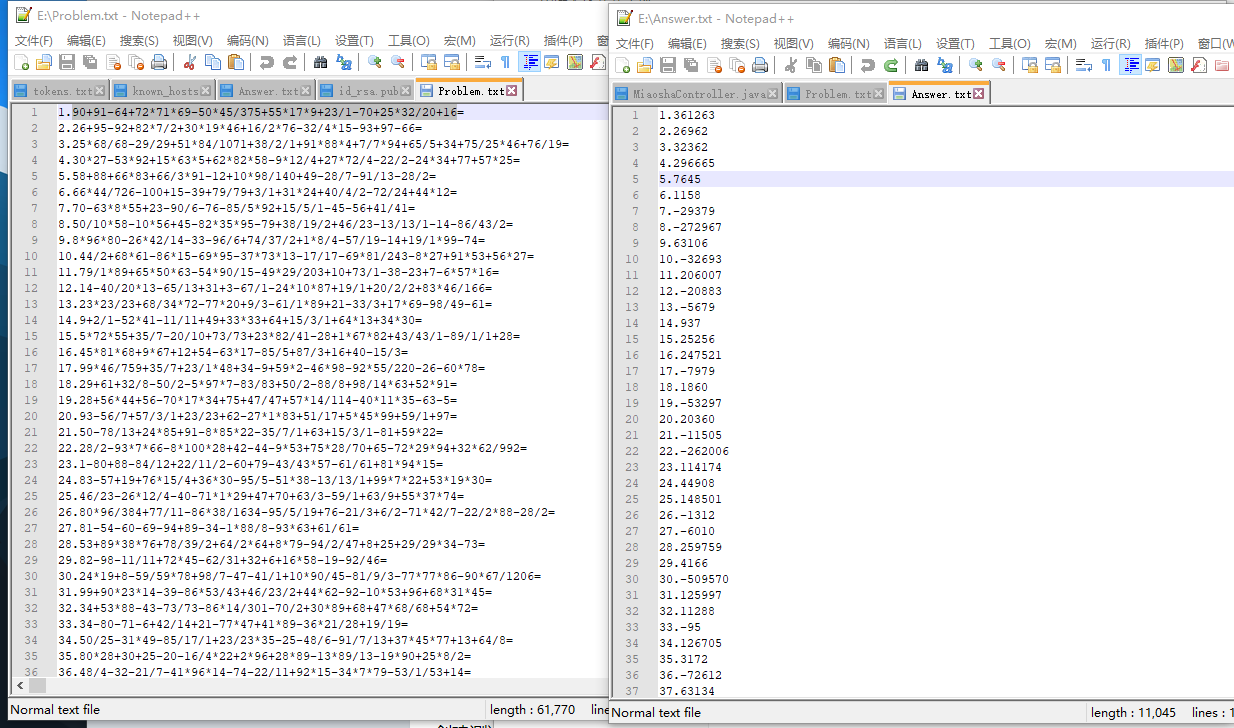
输出到文件

/// <summary>
/// 将题目和答案打印到文件
/// 默认目录 E:\\
/// </summary>
public static void printToFile()
{
    int i = 1000, k = 1;
    string pathProblem = "E:\\Problem.txt", pathAnswer = "E:\\Answer.txt";
    FileStream f1 = new FileStream(pathProblem, FileMode.Create, FileAccess.ReadWrite);
    FileStream f2 = new FileStream(pathAnswer, FileMode.Create, FileAccess.ReadWrite);
    StreamWriter sw1 = new StreamWriter(f1);
    StreamWriter sw2 = new StreamWriter(f2);
    while (i-- > 0)
    {
        Result result = formulaMaker();
        Queue<string> queue = changeToPostfix(result.formulaQueue);
        int res = calculate(queue);
        result.result = res;

        sw1.Write(k + "." + result.infixFormula + "=\r\n");
        sw2.Write(k++ + "." + result.getResult() + "\r\n");
    }
    sw1.Close();
    sw2.Close();
}

单元测试

创建测试项目：

添加引用：

运行测试：和结果相符

效能工具

修改主函数：

public static void Main(string[] args)
{
    for (int i = 0; i < 10000000; i++) {
        Result result = formulaMaker();
        Queue<string> postfixQueue = changeToPostfix(result.FormulaQueue);
        int res = calculate(postfixQueue);
        Console.WriteLine("formula:" + result.infixFormula);
        Console.WriteLine("result:" + res);
    }
}

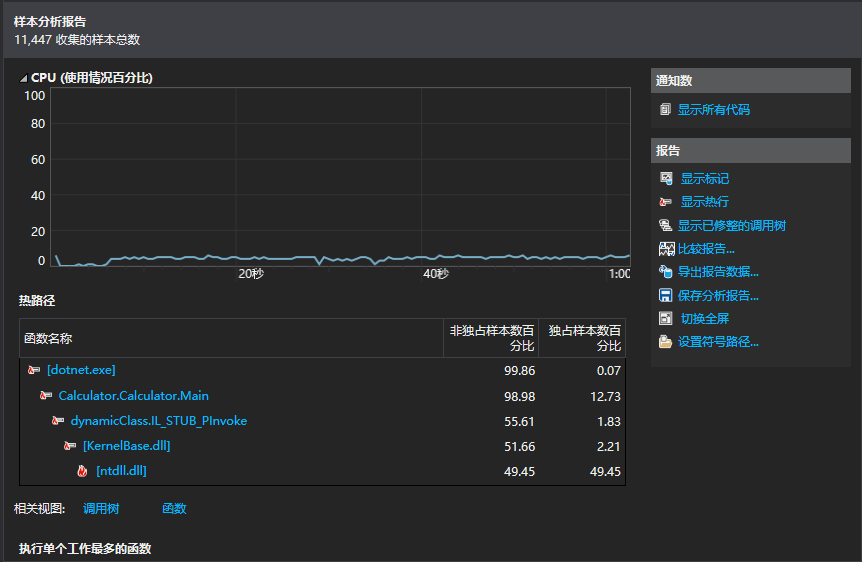
效能分析报告：

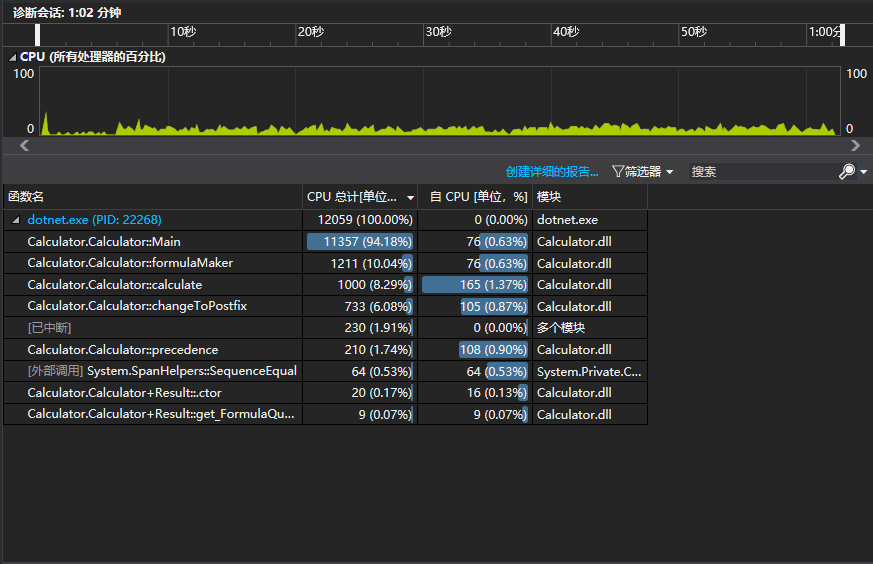
创建详细的报告：

提交代码

40184@Rongz MINGW32 /e/RongGit (master)
$ git add AchaoCalculator
warning: adding embedded git repository: AchaoCalculator
hint: You've added another git repository inside your current repository.
hint: Clones of the outer repository will not contain the contents of
hint: the embedded repository and will not know how to obtain it.
hint: If you meant to add a submodule, use:
hint:
hint:   git submodule add <url> AchaoCalculator
hint:
hint: If you added this path by mistake, you can remove it from the
hint: index with:
hint:
hint:   git rm --cached AchaoCalculator
hint:
hint: See "git help submodule" for more information.

40184@Rongz MINGW32 /e/RongGit (master)
$ git commit -m "release version"
[master (root-commit) 31ec8d9] release version
 1 file changed, 1 insertion(+)
 create mode 160000 AchaoCalculator

创建自己的存储库（略）

这时候执行上面两条语句，git会提示403，也就是无权限访问

因为git不知道你是谁，所以要给git一个公钥，自己留个私钥，具体配置看下面博客：

https://www.cnblogs.com/wmr95/p/7852832.html

之后提交就没有问题了：

40184@Rongz MINGW32 /e/RongGit/AchaoCalculator (master)
$ git push -u origin master
Counting objects: 17, done.
Delta compression using up to 4 threads.
Compressing objects: 100% (14/14), done.
Writing objects: 100% (17/17), 6.70 KiB | 190.00 KiB/s, done.
Total 17 (delta 1), reused 0 (delta 0)
remote: Resolving deltas: 100% (1/1), done.
To github.com:Zrz458/ZrzCalculator.git
 * [new branch]      master -> master
Branch master set up to track remote branch master from origin.

总结

思路比代码重要，思路不对累死狗，思路对了很简单