Tensorflow笔记：激活函数，损失函数，交叉熵

神经元模型：用数学公式表示为：?(∑????? + ?)，f 为激活函数。神经网络是以神经元为基本单 元构成的。 

激活函数：引入非线性激活因素，提高模型的表达力。 

常用的激活函数有 relu、sigmoid、tanh 等。 
① 激活函数 relu: 在 Tensorflow 中，用 tf.nn.relu()表示 

 

 ② 激活函数 sigmoid：在 Tensorflow 中，用 tf.nn.sigmoid()表示

 

③ 激活函数 tanh：在 Tensorflow 中，用 tf.nn.tanh()表示 

 

神经网络的复杂度：可用神经网络的层数和神经网络中待优化参数个数表示 
神经网路的层数：一般不计入输入层，层数 = n 个隐藏层 + 1 个输出层 

 
神经网路待优化的参数：神经网络中所有参数 w 的个数 + 所有参数 b 的个数 

在该神经网络中，包含 1 个输入层、1 个隐藏层和 1 个输出层，该神经网络的层数为 2 层。 
在该神经网络中，参数的个数是所有参数 w 的个数加上所有参数 b 的总数，第一层参数用三行四列的
二阶张量表示（即 12 个线上的权重 w）再加上 4 个偏置 b；第二层参数是四行两列的二阶张量（）即
8 个线上的权重 w）再加上 2 个偏置 b。总参数 = 3*4+4 + 4*2+2 = 26。 

---

损失函数（loss）： 用来表示预测值（y）与已知答案（y_）的差距。在训练神经网络时，通过不断改变神经网络中所有参数，使损失函数不断减小，从而训练出更高准确率的神经网络模型。 
常用的损失函数有均方误差、自定义和交叉熵等。 
均方误差 mse：n 个样本的预测值 y 与已知答案 y_之差的平方和，再求平均值。

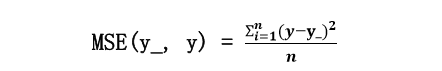
 在 Tensorflow 中用

loss_mse = tf.reduce_mean(tf.square(y_ - y)) 

 

 

---

交叉熵(Cross Entropy)：表示两个概率分布之间的距离。交叉熵越大，两个概率分布距离越远，两个概率分布越相异；交叉熵越小，两个概率分布距离越近，两个概率分布越相似。 

交叉熵计算公式

用 Tensorflow 函数表示为 

ce= -tf.reduce_mean(y_* tf.log(tf.clip_by_value(y, 1e-12, 1.0))) 

例如： 
两个神经网络模型解决二分类问题中，已知标准答案为 y_ = (1, 0)，第一个神经网络模型预测结果为y1=(0.6, 0.4)，第二个神经网络模型预测结果为 y2=(0.8, 0.2)，判断哪个神经网络模型预测的结果更接近标准答案。 

根据交叉熵的计算公式得： 
H1((1,0),(0.6,0.4)) = -(1*log0.6 + 0*log0.4) ≈ -(-0.222 + 0) = 0.222 
H2((1,0),(0.8,0.2)) = -(1*log0.8 + 0*log0.2) ≈ -(-0.097 + 0) = 0.097 
由于 0.222>0.097，所以预测结果 y2 与标准答案 y_更接近，y2 预测更准确。 

softmax 函数：将 n 分类的 n 个输出（y1,y2…yn）变为满足以下概率分布要求的函数。 

 

 

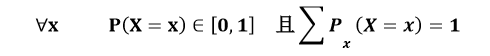
softmax 函数表示为：

 

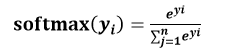
softmax 函数应用：在 n 分类中，模型会有 n 个输出，即 y1,y2…yn，其中 yi 表示第 i 种情况出现的可能性大小。将 n 个输出经过 softmax 函数，可得到符合概率分布的分类结果。 

在 Tensorflow 中，一般让模型的输出经过 sofemax 函数，以获得输出分类的概率分布，再与标准答案对比，求出交叉熵，得到损失函数，用如下函数实现： 
 

ce = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1)) 
cem = tf.reduce_mean(ce)