Dirichlet 前缀和及其应用
全文概要
- Dirichlet 前缀和定义;
- Dirichlet 前缀和的算法,及其拓展;
- Mobius 函数,Mobius 反演以及它们与 Dirichlet 前缀和,Dirichlet 卷积之间关系;
- 具体应用。
1 Dirichlet 前缀和定义
给定数列 \(a_i\),定义数列 \(b_i=\sum\limits_{d|i} a_d\),即所有下标为该下标约数的原数组之和。
例子:\(n=10,a_i=\left\{1,4,6,9,2,4,5,6,4,3\right\}\),则 \(b_i=\left\{1,5,7,14,3,15,6,20,11,10\right\}\)
2 模板问题与复杂度
2.1 Dirichlet 前缀和
2.1.1 算法说明
\(n\le 2\times 10^7\),说明要用优于/微劣于 \(\mathcal{O}(n)\) 的算法。
对于一个数 \(a_j\),它会被计算到 \(b_{1\times j},b_{2\times j}\dots\) 中。
而对于 \(a_k(k\ge 1,k|j)\) ,可以发现会被记入 \(b_{1\times k},b_{2\times k},b_{3\times k}\dots\)
可见 \(b_{1\times j},b_{2\times j}\dots\) 也肯定会被包含;
因此可以得到一个结论:\(b_j\) 会被 \(b_{1\times j},b_{2\times j},b_{3\times j}\dots\) 所包含。
但是如果直接计算 \(b_{4\times j}\),会被 \(b_{j}\) 和 \(b_{2\times j}\) 同时计入,有重复;
于是稍稍变换计算方式:每次乘以一个不超过其下标本身的质数,就可以解决这个问题,也能够保证不重复地计算。
核心代码:
for(int i=1;i<=cnt;i++)
for(int j=1;j*pr[i]<=n;j++) a[j*pr[i]]+=a[j];
其中 cnt 是所有素数的总数,pr[i] 为第 \(i\) 个素数。
2.1.2 算法正确性证明
下面证明上述代码是正确的,也即不重复且不遗漏:
下证第 \(i(i\le cnt)\) 轮过后,对于满足 \(l|d,\frac{d}{l}=pr_1^{\alpha_1}pr_2^{\alpha_2}\dots pr_i^{\alpha_i}\) 的 \(l\),令这些 \(l\) 组成集合 \(S_{i,d}\)。\(b_d=\sum\limits_{l\in S_{i,d}} a_l\)
\(i=0\) 时,显然成立!(\(b_i=a_i\))
假设对 \(i=k-1\) 成立,此时 \(b_1=a_1\),\(j=1\) 成立!
假设 \(b_1\dots b_p\) 均满足如上结论,
\(p=j+1\) 时,如果 \(pr_i|j+1\),那么 \(b_{j+1}\leftarrow b_{j+1}+b_{\frac{j+1}{pr_i}}\),即 \(b_{j+1}=\sum\limits_{l\in{S_{k-1,j+1}}}a_l+\sum\limits_{l\in{S_{k,\frac{j+1}{pr_i}}}}a_l\)
由定义可知 \(S_{k,\frac{j+1}{pr_i}}\cap S_{k-1,j+1}=\varnothing\),且 \(S_{k,\frac{j+1}{pr_i}}\cup S_{k-1,j+1}=S_{k,j+1}\);
所以 \(b_{j+1}=\sum\limits_{l\in{S_{k,j+1}}}a_l\)
得证!
2.1.3 举例验证
举个例子直观地验证一下各个数字的变化情况:\(n=10,cnt=4,pr_i=\left\{2,3,5,7\right\}\)
初始情况:
a1,a2,a3,a4,a5,a6,a7,a8,a9,a10
\(i=1,pr_i=2\) 后:
a1,a2+a1,a3,a4+a2+a1,a5,a6+a3,a7,a8+a4+a2+a1,a9,a10+a5
\(i=2,pr_i=3\) 后:
a1,a2+a1,a3+a1,a4+a2+a1,a5,a6+a3+a2+a1,a7,a8+a4+a2+a1,a9+a3+a1,a10+a5
\(i=3,pr_i=5\) 后:
a1,a2+a1,a3+a1,a4+a2+a1,a5+a1,a6+a3+a2+a1,a7,a8+a4+a2+a1,a9+a3+a1,a10+a5+a2+a1
\(i=4,pr_i=7\) 后:
a1,a2+a1,a3+a1,a4+a2+a1,a5+a1,a6+a3+a2+a1,a7+a1,a8+a4+a2+a1,a9+a3+a1,a10+a5+a2+a1
2.2 Dirichlet 后缀和
类似的,给定数列 \(a_i\),定义数列 \(b_i=\sum\limits_{i|d} a_d\)。
即所有下标为该下标倍数的原数组之和。
我们可以如下操作:每次同样乘以一个不超过其下标本身的质数,但是由于前缀变为后缀,因此把计算顺序改变一下——变成从后向前计算。
为什么呢?画张图。
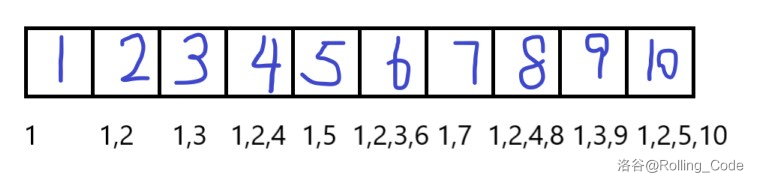
上图为 Dirichlet 前缀和,下面的数字代表给他贡献的 \(a\) 数组下标,上面是 \(b\) 数组下标
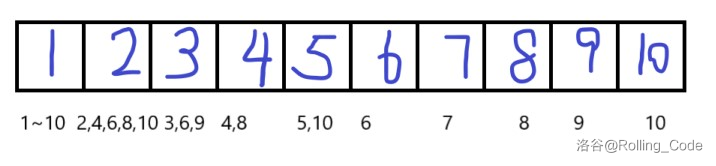
上图为 Dirichlet 后缀和
核心代码:
for(int i=1;i<=cnt;i++)
for(int j=n/pr[i];j>=1;j--) a[j]+=a[j*pr[i]];
用类似 Dirichlet 前缀和的证法也可以得证!
2.3 逆推 Dirichlet 前缀和
即已知前缀和 \(b_i\),求原数组 \(a_i\);
相当于是一个差分(Dirichlet 差分)。
所以直接按照前缀和的代码倒序遍历即可。
核心代码:
for(int i=cnt;i>=1;i--)
for(int j=n/pr[i];j>=1;j--) a[j*pr[i]]-=a[j];
2.4 逆推 Dirichlet 后缀和
即已知前缀和 \(b_i\),求原数组 \(a_i\);
还是 Dirichlet 差分,可以按照后缀和代码倒序遍历。
核心代码:
for(int i=cnt;i>=1;i--)
for(int j=1;j*pr[i]<=n;j++) a[j]-=a[j*pr[i]];
2.5 Dirichlet 前缀和及其拓展复杂度
这个算法复杂度为 \(\mathcal{O}(\sum\limits_{\text{质数p}\le n} \dfrac{n}{p})\),与埃氏筛的复杂度相同,因此可以得知复杂度约为 \(\mathcal{O}(n\log\log n)\)
3 Dirichlet 卷积 和 Mobius 反演
3.1 Dirichlet 卷积 和 Mobius 函数之间的关系
3.1.1 什么是Dirichlet 卷积
Dirichlet 卷积,是定义在两个数论函数 \(f,g\) 上的 \(f*g\) 满足 \((f*g)(n)=\sum\limits_{d|n}f(d)\times g(n/d)\)
Dirichlet 卷积满足如下的规律:
-
交换律:\(f*g=g*f\)
-
结合律:\((f*g)*h=f*(g*h)\)
-
分配律:\(f*(g+h)=f*g+f*h\)
-
存在单位元:定义 \(\epsilon(n)=[n=1]\),则 \(f*\epsilon =f\)
-
保持积性:如果 \(f,g\) 都是积性函数,那么 \(f*g\) 也是积性函数。
3.1.2 什么是 Mobius 函数
Mobius 函数用 \(\mu\) 来表示。
如果 \(n=1\) 则 \(\mu(n)=1\);
如果 \(n\) 没有平方因子,则 \(\mu(n)=(-1)^{\text{n的素因子个数}}\);
如果 \(n\) 有平方因子,则 \(\mu(n)=0\)。
定理一:
即 \(\epsilon=\mu*1\);
证明:
设 \(n=p_1^{\alpha_1}p_2^{\alpha_2}\dots p_k^{\alpha_k},n'=\prod\limits_{i=1}^{k} p_i\)
所以 \(\sum\limits_{d|n} \mu(d)=\sum\limits_{d|n'}\mu(d)=\sum\limits_{i=0}^{k}C^i_k\times (-1)^k=(1+(-1))^k=[n=1]=\epsilon(n)\)
得证!
所以我们可以利用 Dirichlet 卷积处理 Mobius 函数!
3.1.3 莫比乌斯反演
如果函数 \(f,g\) 满足
则
证明:根据定义可以得到 \(f=g*1\)
两边同时卷上 \(\mu\)
可以得到:
因为 \(\mu(p^k)=[k=1]\),而且 \(\mu\) 是积性函数,所以可以用线性筛模板计算。
void prime(ll n){
mu[1]=1;
for(int i=2;i<=n;i++){
if(!vst[i]) pr[++cnt]=i,mu[i]=-1;
for(ll j=1;j<=cnt&&i*pr[j]<=n;j++){
vst[i*pr[j]]=1;
if(!(i%pr[j])){mu[i*pr[j]]=0;break;}
mu[i*pr[j]]=-mu[i];
}
}
}
3.2 复杂度的分析
假设我们现在要算 \(f=g*1\),如果对于每一个 \(f_i\) 都是暴力计算,复杂度是 \(\mathcal{O}(\sqrt n)\) 的,总和是 \(\mathcal{O}(n\sqrt n)\);
如果预计算完了每个数的约数列表,可以得知复杂度约为 \(\mathcal{O}(n/1+n/2+\dots n/n)\),而每个数计算也需要其约数个数的复杂度。
而 \(\lim\limits_{n\rightarrow \infty}\sum\limits_{i=1}^{n}\dfrac{n}{i}=n\ln n\)(素数定理)
所以预计算约数的复杂度总和是 \(\mathcal{O}(n\log n)\)。
而我们使用了 Dirichlet 卷积以后复杂度下降为 \(\mathcal{O}(n\log \log n)\)。
主要的差距就在于 Dirichlet 卷积以后我们省去了重新计算 \(f_d(d|i)\) 的过程。
举个例子:在前两种情况,计算 \(f_{10}\) 时,前两种方法都会将 \(f_5\) 重新计算,但是事实上在 Dirichlet 卷积当中 之前计算好的 \(f_5\) 可以被重复利用,进而减少计算次数。
3.3 从多维空间看 Dirichlet 前缀和
我们回过头来看一看 \(n=10\) 时最后的 \(b_i\):
a1,a2+a1,a3+a1,a4+a2+a1,a5+a1,a6+a3+a2+a1,a7+a1,a8+a4+a2+a1,a9+a3+a1,a10+a5+a2+a1
乍看之下似乎没有规律。
如果我们将 \(i\) 质因数分解以后,并且以各个质因数的幂次作为坐标呢?

举个比较形象的例子:(为了表示方便暂时只列出前三根轴)红色线条框出的立方体即为 \(b_{30}\) 所包含的所有 \(a_d\) 在这个空间中的坐标,而蓝色框出的部分即为 \(b_{100}\) 所包含的 \(a_d\)。
如果我们要在这个空间内做差分的话,由容斥原理,令 \(n=p_1^{\alpha_1}p_2^{\alpha_2}\dots p_k^{\alpha_k}\) 可得
由 Mobius 函数的定义,如果存在平方的质数为 \(n\) 约数,\(\mu(n)=0\)。
这就是 Dirichlet 差分!
再看一下 Mobius 反演的式子:
会发现 Dirichlet 差分和 Mobius 反演本质一样。
借此发现了 Dirichlet 前缀和/差分 与 Mobius 反演之间的关系。
4 具体的应用
即求
设 \(g(x)\) 为 \(\gcd(i,j)=x\) 的个数,\(f(x)\) 为 \(\gcd(i,j)=k\times d,k=1,2,\dots\) 的个数。(假设是单组数据)
即求
把 \(g(p)\) 的表达式代入。
可以使用莫比乌斯反演!
改变枚举项,枚举
把 \(
d\times p\) 换元成
\(T\) 可以得到:
再交换一下 \(\sum\) 的顺序:
所以就可以线性筛 \(\mu\) 函数,整除分块并记录前缀和。
复杂度 \(\mathcal{O}(n+\sqrt{n})\)。
4.后记
通过 Dirichlet 前缀和,构建起了 Mobius 函数,Mobius 反演,及高维前缀和的关系。
但是 Dirichlet 前缀和不仅在计算机中有所应用,数学中也可以见到他的身影。
比如在证明与 \(\varphi\) 等数论函数相关的式子里,可以派上用场。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号