9.22 闲话

拉格朗日插值可以看作是 CRT 在多项式上的扩展，所以通过 CRT 在模意义下的推导在此不表 .

我们有若干点值 \((x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)\)，拉格朗日插值可以通过 \(n\) 个点值来确定一个 \(\deg\le n-1\) 的多项式 .

核心就是要构造一个多项式同时通过这些点值 .

假设要构造的函数为 \(f(x)\)，那么可以将其拆成若干函数：

\[f(x)=\sum_{i=1}^nf_i(x) \]

其中 \(f_i(x)\) 的定义为：

\[f_i(x_j)= \begin{cases} y_j&(j= i)\\ 0&(j\ne i) \end{cases} \]

容易发现，\(f_i(x)\) 中一定含有 \(\prod_{j\ne i}(x-x_j)\) 项，再进行代入可以得到 \(\displaystyle f_i(x)=y_i\prod_{j\ne i}\frac{x-x_j}{x_i-x_j}\) .

最后代入即可得到拉格朗日插值公式：

\[\sum_{i=1}^ny_i\prod_{j\ne i}\frac{x-x_j}{x_i-x_j} \]

来几道例题：

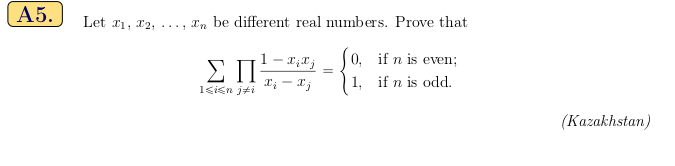
看上去很拉插，实际上标算之一也是拉插，但是太过巧妙，本人想不出来 .

如果有一个 \(x_i\in\{1,-1\}\) 的话是好验证的 .

构造以下函数：

\[f(x)=\prod_{i=1}^{n}(1-x_ix) \]

然后注意到：

\[f(x_i)=(1-x_i^2)\prod_{j\ne i}(1-x_ix_j) \]

然后对 \(x_1,\dots,x_n\) 和 \(\pm 1\) 处的 \(f\) 点值进行拉格朗日插值：

\[f(x)=\sum_{i=1}^nf(x_i)\frac{(x-1)(x+1)}{(x_i-1)(x_i+1)}\prod_{j\ne i}\frac{x-x_j}{x_i-x_j}+f(1)\frac{x+1}{1+1}\prod_{1\leqslant i \leqslant n}\frac{x-x_i}{1-x_i}+f(-1)\frac{x-1}{-1-1}\prod_{1\leqslant i \leqslant n}\frac{x-x_i}{1-x_i} \]

然后发现，我们插出来了一个 \(\deg\le n+1\) 的多项式，但是 \(\deg(f)\le n\)，这说明 \(x^{n+1}\) 系数为 \(0\)，所以对这项提取系数：

\[\begin{aligned} 0&=\sum_{1\leqslant i \leqslant n}\frac{f(x_i)}{\prod_{j\ne i}(x_i-x_j)\cdot(x_i-1)(x_i+1)}+\frac{f(1)}{\prod_{1\leqslant j \leqslant n}(1-x_j)\cdot(1+1)}+\frac{f(-1)}{\prod_{1\leqslant j \leqslant n}(-1-x_j)\cdot(-1-1)}\\ &=-\sum_{1\leqslant i \leqslant n}\prod_{j\ne i}\frac{1-x_ix_j}{x_i-x_j}+\frac 12+\frac{(-1)^{n+1}}2 \end{aligned} \]

然后就做完了 .