【BZOJ2127】happiness
Time Limit: 1000 ms Memory Limit: 256 MB
Description
高一一班的座位表是个n*m的矩阵,经过一个学期的相处,每个同学和前后左右相邻的同学互相成为了好朋友。这学期要分文理科了,每个同学对于选择文科与理科有着自己的喜悦值,而一对好朋友如果能同时选文科或者理科,那么他们又将收获一些喜悦值。作为计算机竞赛教练的scp大老板,想知道如何分配可以使得全班的喜悦值总和最大。
Input
第一行两个正整数n,m。接下来是六个矩阵第一个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择文科获得的喜悦值。第二个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择理科获得的喜悦值。第三个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择文科获得的额外喜悦值。第四个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择理科获得的额外喜悦值。第五个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择文科获得的额外喜悦值。第六个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择理科获得的额外喜悦值。
Output
输出一个整数,表示喜悦值总和的最大值
Sample Input
1 1
100 110
1
1000
Sample Output
【样例说明】
两人都选理,则获得100+110+1000的喜悦值。
【数据规模】
对于100%以内的数据,n,m<=100 所有喜悦值均为小于等于5000的非负整数
Solution
这种相邻格子的问题,一般都是考虑两个相邻的格子的最小割模型,然后把所有模型叠加起来。
现在考虑相邻的两人$x$和$y$。$x$选文或理的收益是$x_0,x_1$;$y$选文或理的收益是$y_0,y_1$;都选文的收益是$s_0$,都选理的收益是$s_1$。
那么从总收益$sum=x_0+x_1+y_0+y_1+s_0+s_1$中减去最小割就是最优解。
考虑一下逻辑关系:
(1)如果$x$和$y$都选文,那么需要割去$x_1,y_1,s_1$
(2)如果$x$和$y$都选理,那么需要割去$x_0,y_0,s_0$
(3)如果$x$文$y$理,那么需要割去$x_1,y_0,s_0,s_1$
(4)如果$x$理$y$文,那么需要割去$x_0,y_1,s_0,s_1$
发现一个人选一科,必定割掉另外一科的喜悦值。那么由源点$S$向$x$连$x_0$的边,向$y$连$y_0$的边;$x$向汇点$T$连$x_1$的边,向$y$连$y_1$的边。
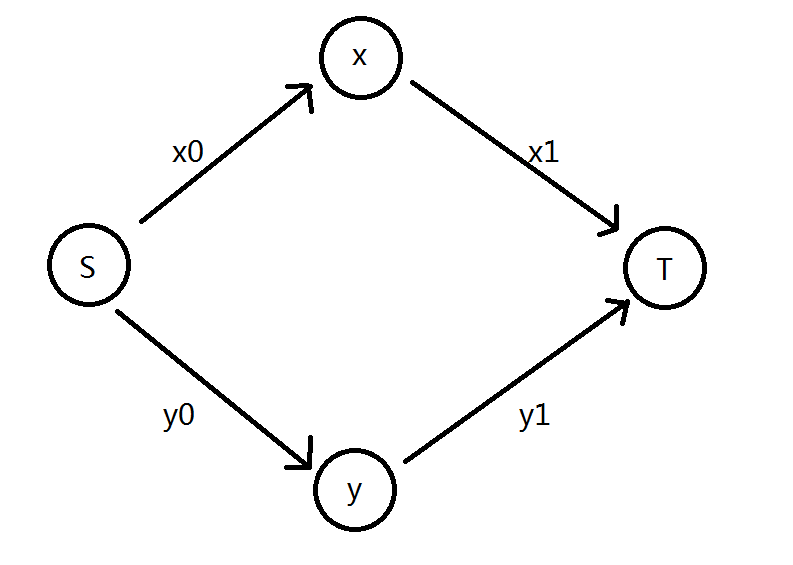
现在,(1)和(2)还差$s_0$和$s_1$未刻画。因为割掉两条边以后貌似图就彻底分开了,不好再加入新的边来体现,我们考虑将$s_0$附加在$x_0$与$y_0$上,将$s_1$附加在$x_1$与$y_1$上,即各分一半:
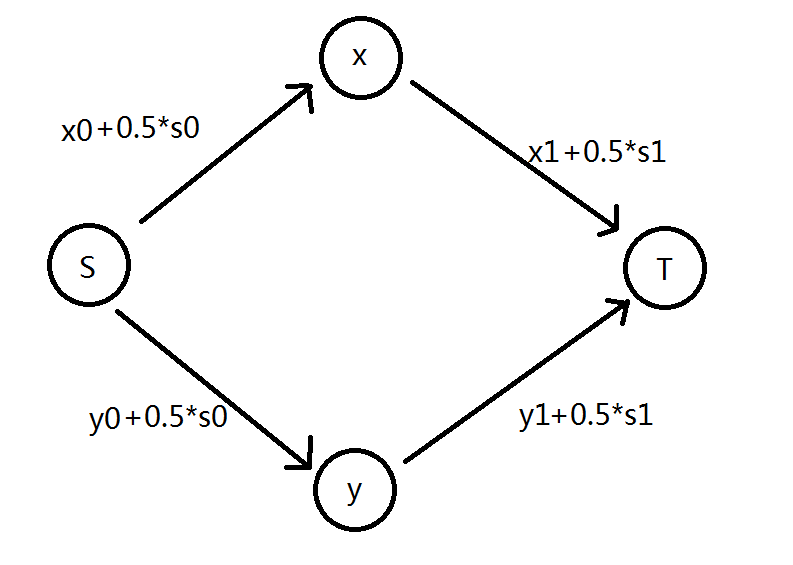
(1)和(2)刻画完毕。但是(3)和(4)在其中不适用了。
如果$x$选文,$y$选理,那么割去的边是右上和左下两条边,其权值之和是$x_1+\frac{1}{2}s_1+y_0+\frac{1}{2}s_0$,但是我们期望的是$x_1+y_0+s_0+s_1$,不对啊。
怎么办?期望值和当前值一作差,得$\frac{1}{2}s_0+\frac{1}{2}s_1=\frac{1}{2}(s_0+s_1)$。想办法把它实例化!当割去的是右上和左下两条边时,已经形成最小割,那么强行把这条边塞进去!由$y$向$x$连一条权值为$\frac{1}{2}(s_0+s_1)$的调整边即可。
$x$理$y$文同理。
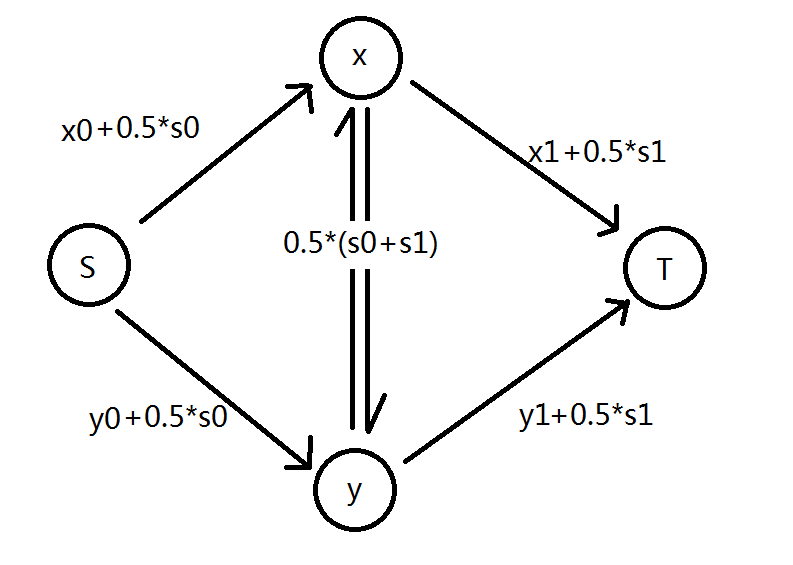
中间的两条调整边,仅在二者文理不同的时候起作用。现在这个模型,已经可以刻画(1)~(4)所有的情况了。
对全图进行建模,跑出最小割,用总收益和减去最小割即可。
Important:
我们不能对于每两个格子都像如上模型一样连接$(S,x),(S,y),(x,T),(y,T)$,将总收益和看做每两个格子的$sum$之和,然后将模型并起来跑。
为什么?因为这样我们会发现某一些$x_0$、$x_1$和$y_0$、$y_1$被多算了几次,这是极不好的,模型之间出现了交集。
事实上对于一个点$x$,我们将所有$S$->$x$的边都合并起来:即权值应该为:$x_0$或$y_0$加上$\frac{1}{2} \sum s_0$。$x$到$T$的边同理。
而中间的调整边照常即可。
这样当$sum$为所有格子的收益和的时候,用$sum$减去最小割的答案是对的。
Tips:
可以将边权乘上2,跑出最小割后除以2,即可忽略小数。

#include <cstdio> #include <queue> using namespace std; const int N=10010,INF=2147000000; int n,m,a[110][110],b[110][110],ax[110][110],ay[110][110],bx[110][110],by[110][110]; int sum; int S,T,dis[N],cur[N],h[N],tot; queue<int> q; struct Edge{int v,next,f;}g[N*20]; inline int id(int x,int y){return (x-1)*m+y;} inline int min(int x,int y){return x<y?x:y;} inline void addEdge(int u,int v,int f){ g[++tot].v=v; g[tot].f=f; g[tot].next=h[u]; h[u]=tot; g[++tot].v=u; g[tot].f=0; g[tot].next=h[v]; h[v]=tot; } bool bfs(){ while(!q.empty()) q.pop(); q.push(S); for(int i=1;i<=T;i++) dis[i]=-1; dis[S]=0; while(!q.empty()){ int u=q.front(); q.pop(); for(int i=h[u],v;i;i=g[i].next) if(g[i].f&&dis[v=g[i].v]==-1){ dis[v]=dis[u]+1; if(v==T) return true; q.push(v); } } return dis[T]!=-1; } int dfs(int u,int delta){ if(u==T) return delta; int ret=0,get; for(int i=cur[u],v;i&δi=g[i].next) if(g[i].f&&dis[v=g[i].v]==dis[u]+1){ get=dfs(v,min(delta,g[i].f)); g[i].f-=get; g[i^1].f+=get; if(g[i].f) cur[u]=i; delta-=get; ret+=get; } if(!ret) dis[u]=-1; return ret; } int dinic(){ int ret=0; while(bfs()){ for(int i=1;i<=T;i++) cur[i]=h[i]; ret+=dfs(S,INF); } return ret; } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&a[i][j]),sum+=a[i][j]; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&b[i][j]),sum+=b[i][j]; for(int i=1;i<n;i++) for(int j=1;j<=m;j++) scanf("%d",&ax[i][j]),sum+=ax[i][j]; for(int i=1;i<n;i++) for(int j=1;j<=m;j++) scanf("%d",&bx[i][j]),sum+=bx[i][j]; for(int i=1;i<=n;i++) for(int j=1;j<m;j++) scanf("%d",&ay[i][j]),sum+=ay[i][j]; for(int i=1;i<=n;i++) for(int j=1;j<m;j++) scanf("%d",&by[i][j]),sum+=by[i][j]; S=n*m+1; T=n*m+2; tot=1; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ int u=id(i,j); addEdge(S,u,a[i][j]*2+ax[i-1][j]+ax[i][j]+ay[i][j-1]+ay[i][j]); addEdge(u,T,b[i][j]*2+bx[i-1][j]+bx[i][j]+by[i][j-1]+by[i][j]); if(i<n){ addEdge(u,id(i+1,j),ax[i][j]+bx[i][j]); addEdge(id(i+1,j),u,ax[i][j]+bx[i][j]); } if(j<m){ addEdge(u,id(i,j+1),ay[i][j]+by[i][j]); addEdge(id(i,j+1),u,ay[i][j]+by[i][j]); } } int get=dinic(); get/=2; printf("%d\n",sum-get); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号