【BZOJ3218】 a+b Problem

---

 

Solution

　　看一下如何建最小割模型：

　　先求$sum=\sum b_i+w_i$。

　　如果某一个格子$i$选择了黑色，那么贡献是$-w_i$；如果满足是它奇怪的格子，还有额外贡献$-p_i$。

　　如果选择了白色，那么贡献是$-b_i$。

　　总贡献加上$sum$就是答案。

 

　　对于如上条件，可以对每一个格子建立一个单元：

    

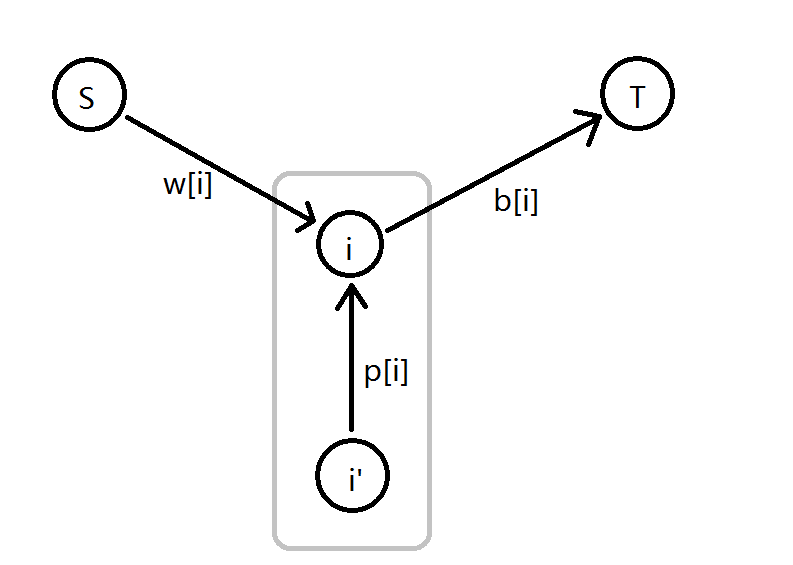
　　可以发现，如果选择白色，那么直接割去$b[i]$这条边。那么要怎么影响之后的黑格呢？

　　对于每一个点$i$，对于所有的$j>i$，使得$i$按题目要求可以使$j$成为奇怪的格子，那么由$i$向$j'$连一条$\infty$的边。

　　如果第$i$个格子选择白色，那么对$j$的单元来说，必须割掉$p[j]$这条边，加上原本一定要割的$w[j]$，就是$j$成为奇怪格子的贡献。　

　　由此建模完成。

 

　　但是边数高达$O(n^2)$

　　看看题目的要求是$i<j$，也就是说对于格子$i$，在$1...i-1$的范围内找权值为$[l_i,r_i]$的格子，对单元进行连接。

　　看起来好像主席树啊，那就关于$a_i$建权值主席树吧。

　　类似线段树优化网络流建边地，往主席树插入第$i$个格子的时候，将$i$（单元里面的那个$i$点）连向新链上每一个新节点，再由原节点连向新节点，流量都是$\infty$。

　　注意不能像平时用线段树跑网络流一样在叶子底部连接，然后从儿子往父亲流。因为这样会出现版本的冲突。

　　跑一下就好了。

　　PS:边的计数器忘记初始化调了整整一个上午服了。。。

　　

---

#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int N=5010,NS=100010,INF=2147000000;
int n,a[N],b[N],w[N],lb[N],rb[N],p[N],sum;
int h[NS],tot,cnt,root[N];
int list[NS],ltot,maxs;
int ch[NS][2];
int S,T,dis[NS],cur[NS];
queue<int> q;
struct Edge{int v,f,next;}g[1000010];
inline void addEdge(int u,int v,int f){
    g[++tot].v=v; g[tot].f=f; g[tot].next=h[u]; h[u]=tot;
    g[++tot].v=u; g[tot].f=0; g[tot].next=h[v]; h[v]=tot;
}
void lsh(){
    sort(list+1,list+1+ltot);
    ltot=unique(list+1,list+1+ltot)-list-1;
    maxs=ltot;
    for(int i=1;i<=n;i++){
        a[i]=lower_bound(list+1,list+1+ltot,a[i])-list;
        lb[i]=lower_bound(list+1,list+1+ltot,lb[i])-list;
        rb[i]=lower_bound(list+1,list+1+ltot,rb[i])-list;
    }
}
int copy(int u){
    int v=++cnt;
    ch[v][0]=ch[u][0]; ch[v][1]=ch[u][1];
    if(u)
        addEdge(u,v,INF);
    return v;
}
void insert(int u,int &v,int l,int r,int pos,int who){
    v=copy(u);        
    addEdge(who*2-1,v,INF);
    if(l==r) return;
    int mid=(l+r)>>1;
    if(pos<=mid)
        insert(ch[u][0],ch[v][0],l,mid,pos,who);
    else
        insert(ch[u][1],ch[v][1],mid+1,r,pos,who);
}
void link(int u,int l,int r,int L,int R,int node){
    if(!u) return;
    if(L<=l&&r<=R){
        addEdge(u,node,INF);
        return;
    }
    int mid=(l+r)>>1;
    if(R<=mid) link(ch[u][0],l,mid,L,R,node);
    else if(mid<L) link(ch[u][1],mid+1,r,L,R,node);
    else{
        link(ch[u][0],l,mid,L,mid,node);
        link(ch[u][1],mid+1,r,mid+1,R,node);
    }
}
bool bfs(){
    while(!q.empty()) q.pop();
    q.push(S);
    for(int i=1;i<=cnt;i++) dis[i]=-1;
    dis[S]=0;
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(int i=h[u],v;i;i=g[i].next)
            if(g[i].f&&dis[v=g[i].v]==-1){
                dis[v]=dis[u]+1;
                if(v==T) return true;
                q.push(v);
            }
    }
    return dis[T]!=-1;
}
int dfs(int u,int delta){
    if(u==T) return delta;
    int ret=0,get;
    for(int i=cur[u],v;i&&delta;i=g[i].next)
        if(g[i].f&&dis[v=g[i].v]==dis[u]+1){
            get=dfs(v,min(delta,g[i].f));
            g[i].f-=get;
            g[i^1].f+=get;
            if(g[i].f) cur[u]=i;
            delta-=get;
            ret+=get;
        }
    if(!ret) dis[u]=-1;
    return ret;
}
int dinic(){
    int ret=0;
    while(bfs()){
        for(int i=1;i<=cnt;i++) cur[i]=h[i];
        ret+=dfs(S,INF);
    }
    return ret;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d%d%d%d%d",&a[i],&b[i],&w[i],&lb[i],&rb[i],&p[i]);
        list[++ltot]=a[i];
        list[++ltot]=lb[i];
        list[++ltot]=rb[i];
        sum+=b[i]+w[i];
    }
    lsh();
    S=n*2+1; T=n*2+2;
    tot=1;
    for(int i=1;i<=n;i++){
        cnt+=2;
        addEdge(cnt,cnt-1,p[i]);
        addEdge(S,cnt-1,w[i]);
        addEdge(cnt-1,T,b[i]);
    }
    cnt+=2;
    for(int i=1;i<=n;i++)
        insert(root[i-1],root[i],1,maxs,a[i],i);    
    for(int i=2;i<=n;i++)
        link(root[i-1],1,maxs,lb[i],rb[i],i*2);
    int get=dinic();
    printf("%d\n",sum-get);
    return 0;
}