【CF 678F】Lena and Queries

 

Time Limit: 2000 ms   Memory Limit: 512 MB

 

Description

　　初始有一个空集合

　　n个操作

　　有三种操作，如下:
　　1 a b 表示向集合中插入二元组(a,b)
　　2 i 表示删除第i次操作时所插入的二元组
　　3 q 表示询问当前集合的二元组中，$(a*q+b)$最大是多少

Input

　　第一行一个整数$n$，表示操作个数

　　接下来$n$行，每行表示一个操作，格式见上

Output

　　对于每个询问输出一行表示最大值

　　如果询问时集合为空，输出 EMPTY SET

Sample Input

　　7
　　3 1
　　1 2 3
　　3 1
　　1 -1 100
　　3 1
　　2 4
　　3 1

Sample Output

　　EMPTY SET
　　5
　　99
　　5

Hint

　　对于操作$2~i$，数据保证第$i$次操作的类型为$1$，且之前未被删除,且不会删除仍未进行的操作　
　　对于$10\%$的数据,$1\le n\le 5000$
　　对于$30\%$的数据,$1\le n\le 50000$
　　对于$100\%$的数据,$1\le n\le 3*10^5,~~-10^9\le a,b,q\le 10^9$

 

 

---

题解

先考虑点集不变的情况：

　　我们设$x=q*a+b$，那么目标就是在集合中找到最大的$k$。

　　移一下项：$b=-q*a+x$，现在的目标变为，对于每一个$(a,b)$的点对画一条斜率为$q$的直线，最大化截距。

　　就像平移一样，如下图所示，黑点代表一个$(a,b)$，橙点代表其所对应的截距，也就是$(a*q+b)$：

　　

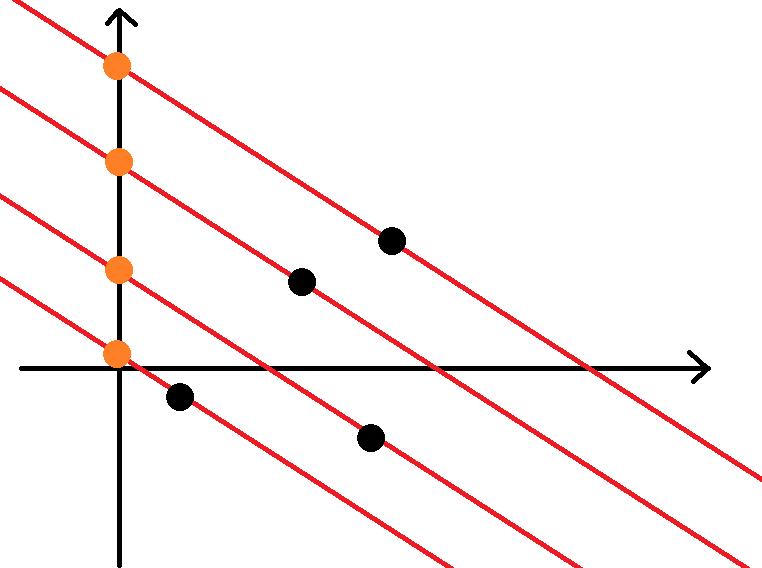
　　我们要最大化截距，而直线都是平行地平移来平移去，直线斜率的正负已经不重要了，取上凸壳的点才有可能是最优解：

　　

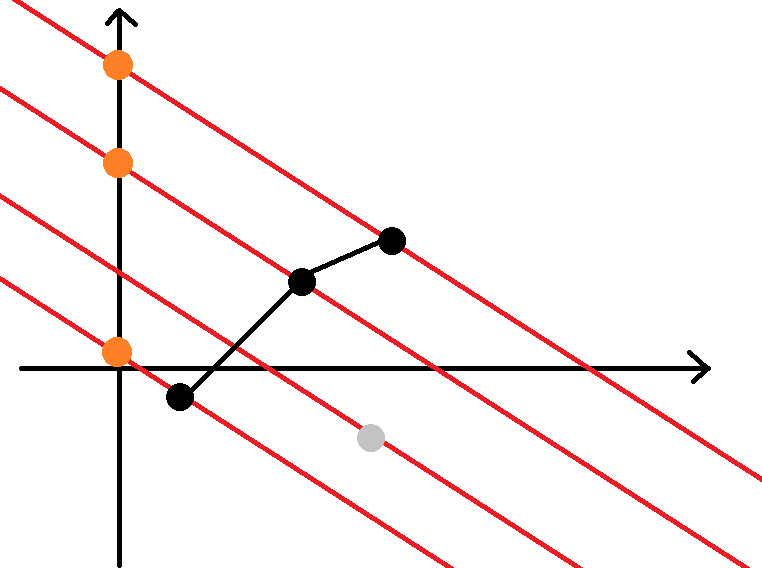
　　注意并不是取上凸壳最高的点就是最优解，拿上图的最右上角的黑点举例，在另一个例子中，反倒是经过另一个点的直线截距最大：

　　

　　但是不管怎样，如果从左到右看上凸壳的点，截距的变化是一个单峰函数。

　　那么我们就可以在上凸壳进行三分（以每一个点的截距为关键值）。

 

点集的变化？

 　   建立一棵以时间为下标的线段树，每一个线段树节点都有一个上凸壳，包含在这个节点代表的时间段内，出现的所有点对。

　　每一个点对$(a,b)$有一个存在区间$[l,r]$，对于线段树上$[l,r]$覆盖的线段树节点，往它们里面都加入该点对。

　　对于查询操作，若在时间$i$询问$q$，就从根节点遍历到下标为$[i,i]$的叶子节点。在路上的每一个节点，都在它的上凸壳内进行一次三分（代入$q$），最后取所有经过的点的最大值即可。

　　为什么？因为在访问$[i,i]$的时候经过了一个节点$u$，那么$u$一定包含$[i,i]$。所以对所有经过节点三分，一定考虑到了询问$i$时还活着的所有点对。

 

　　维护上凸壳时，由于单调栈的模拟需要$a$递增，如果每一个节点插完之后自己再排序就太慢了。可以先离线记录所有的点对，按$a$递增排序，逐个插入线段树，这样就省去了每个节点内部的排序，因为插入的点的$a$一定不会小于整个线段树先前存在的任意一个$a$。

 

　　感觉是道神题orz

　　

---

#include <cstdio>
#include <cstring>
using namespace std;
const int N=5010,INF=2139062143;
int n,h[N],tot,d[N],root,all,sum[N];
int f[N][2][N/2];
struct Edge{int v,next;}g[N*2];
inline int min(int x,int y){return x<y?x:y;}
inline void upd(int &x,int y){if(y<x) x=y;}
inline void addEdge(int u,int v){g[++tot].v=v; g[tot].next=h[u]; h[u]=tot;}
inline int rd(){
    char c=getchar(); int x=0;
    while(c<'0'||c>'9') c=getchar(); x=c-'0';
    while('0'<=(c=getchar())&&c<='9') x=x*10+c-'0';
    return x;
}
void init(){
    for(int u=1;u<=n;u++)
        if(d[u]==1) all++;
        else if(!root) root=u;
    for(int i=1;i<=n;i++)
        for(int j=0;j<=1;j++)
            for(int k=0,up=all/2;k<=up;k++) f[i][j][k]=INF;
}
void dfs(int u,int fa){
    if(d[u]==1){
        f[u][0][1]=f[u][1][0]=0;
        sum[u]=1;
        return;
    }
    for(int i=h[u],v;i;i=g[i].next)
        if((v=g[i].v)!=fa){
            dfs(v,u);
            sum[u]+=sum[v];
        }
    int fson=0;    
    for(int i=h[u],v;i;i=g[i].next)
        if((v=g[i].v)!=fa){
            if(!fson){
                for(int j=0,up=min(min(sum[u],sum[v]),all/2);j<=up;j++){
                    f[u][0][j]=min(f[v][0][j],f[v][1][j]+1);
                    f[u][1][j]=min(f[v][0][j]+1,f[v][1][j]);
                }
                fson=1;
                continue;
            }
            int F0,F1;
            for(int j=min(sum[u],all/2);j>=0;j--){
                f[u][0][j]+=min(f[v][0][0],f[v][1][0]+1);
                f[u][1][j]+=min(f[v][0][0]+1,f[v][1][0]);
                for(int k=1,upk=min(sum[v],j);k<=upk;k++){
                    upd(f[u][0][j],f[u][0][j-k]+min(f[v][0][k],f[v][1][k]+1));
                    upd(f[u][1][j],f[u][1][j-k]+min(f[v][0][k]+1,f[v][1][k]));
                }
            }
        }
}
int main(){
    n=rd();
    for(int u,v,i=1;i<n;i++){
        u=rd(); v=rd();
        addEdge(u,v); addEdge(v,u);
        d[u]++; d[v]++;
    }
    if(n==2){puts("1"); return 0;}
    init();
    if(all&1) return 0;
    dfs(root,0);
    printf("%d\n",min(f[root][0][all/2],f[root][1][all/2]));
    return 0;
}