银河之星 （乱搞+记忆化搜索）
Time Limit: 1000 ms Memory Limit: 256 MB
Description
题解
乍一看真的无从下手，规则一脸懵逼。
首先看到第3个规则，每个棋子往任意方向都只能走3格。可以联想一下国际象棋四个象，2个永远在黑格，2个永远在白格。
依照这个思路，我们只有9类位置（横坐标模3与纵坐标模3都相同的位置为同一类）。
其中，每一类位置上的棋子可以通过规则3互达同一类位置，却永远不可能用规则3走到其他类的位置。
如下图：（想象若干个3x3的框，左上角对齐铺满整个地图，框内位置相同的即同类位置）
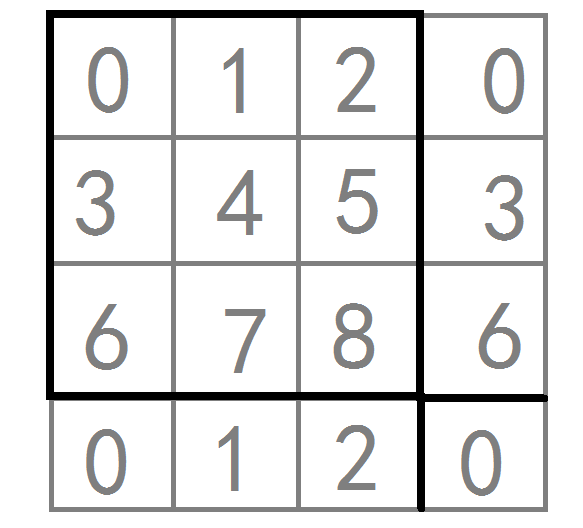
我们把同类位置的棋子数量求和一下，对应放到一个3x3的九宫格里（我们按照上图以0~8为每类位置编号）。以下就只对这个九宫格操作就可以了，比如$x$个0类的棋子越过1个8类棋子到达4类位置，我们把0的数字减$x$，把8的数字减$x$，把4的数字加$x$。
为什么不用考虑实际上棋子的位置呢？
根据上面标红的性质，任意同类棋子可以互达。我不需要考虑我要操作的3枚棋子具体在什么地方，只要将这3枚棋子移到三点一线，就可以进行规则2的操作了。
没完
然而不是每三个位置都能移成三点一线的，受地图大小影响，可能会出现这种情况：
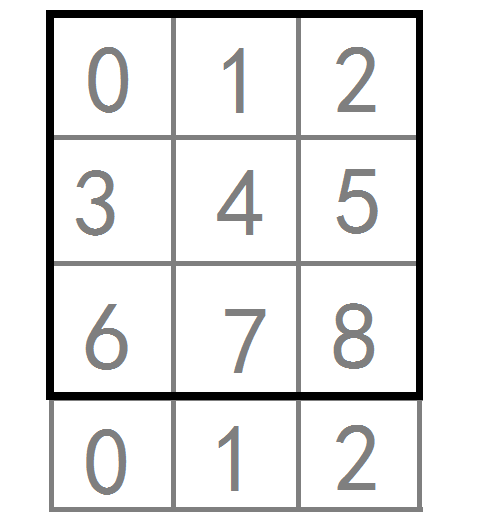
比如这个案例，对于7-->8-->6的情况，我能用九宫格的数字相加减吗？7-->5-->0呢？都不行。因为实际地图上，并不存在一个786、750三点一线的地方。但是0-->6-->3、1-->7-->4、0-->7-->5都是可以用九宫格的数字进行加减操作的，因为地图的确存在这种场所可以供棋子移动过来进行操作。
那么我们预处理出那些类别的位置可以走2步互达（枚举原图的位置往八个方向走2步看看走到的是什么类别的位置）。
考虑到棋子总数只有10，我们可以用状态压缩记录这个九宫格的状态，暴力枚举即可，用map记忆一下有没有到过这个状态。
终止状态即：指定终点同类位置的权值为1，且其他位置权值为0.
1 #include <cstdio> 2 #include <map> 3 #define min(a,b) (a<b?a:b) 4 using namespace std; 5 typedef long long ll; 6 const int base=11,xx[8]={-1,-1,-1,0,0,1,1,1},yy[8]={-1,0,1,-1,1,-1,0,1}; 7 int k,n,m,x0,y0; 8 int can[9][9]; 9 ll bin[10],bigsta,finsta; 10 map<ll,int> ans; 11 inline int trans(int x){return x%3;} 12 void getDirection(){ 13 for(int i=0;i<9;i++) 14 for(int j=0;j<9;j++) can[i][j]=0; 15 int u,v,x,y; 16 for(int i=0;i<n;i++) 17 for(int j=0;j<m;j++){ 18 u=trans(i)*3+trans(j); 19 for(int k=0;k<8;k++){ 20 x=i+xx[k]*2; y=j+yy[k]*2; 21 if(x<0||x>=n||y<0||y>=m) continue; 22 v=trans(x)*3+trans(y); 23 can[u][v]=can[v][u]=1; 24 } 25 } 26 } 27 bool dfs(ll s){ 28 if(s==finsta) return true; 29 if(ans[s]) return ans[s]==1; 30 int now[3][3]; 31 ll t=s; 32 for(int i=8;i>=0;i--){ 33 now[i/3][i%3]=t/bin[i]; 34 t%=bin[i]; 35 } 36 int u,v,p,x,y,px,py; 37 for(int i=0;i<3;i++) 38 for(int j=0;j<3;j++){ 39 u=i*3+j; 40 for(int k=0;k<8;k++){ 41 px=i+xx[k]; py=j+yy[k]; 42 x=i+xx[k]*2; y=j+yy[k]*2; 43 px=(px+9)%3; py=(py+9)%3; x=(x+9)%3; y=(y+9)%3; 44 p=px*3+py; v=x*3+y; 45 if(!can[u][v]) continue; 46 int delta=min(now[i][j],now[px][py]); 47 for(int g=1;g<=delta;g++) 48 if(dfs(s-bin[p]*g-bin[u]*g+bin[v]*g)) return true; 49 } 50 } 51 ans[s]=2; 52 return false; 53 } 54 int main(){ 55 bin[0]=1; 56 for(int i=1;i<=9;i++) bin[i]=bin[i-1]*base; 57 while(~scanf("%d%d%d%d%d",&k,&n,&m,&x0,&y0)){ 58 ans.clear(); 59 x0=trans(x0-1); y0=trans(y0-1); 60 finsta=bin[x0*3+y0]; 61 getDirection(); 62 bigsta=0; 63 for(int i=1,x,y;i<=k;i++){ 64 scanf("%d%d",&x,&y); 65 x=trans(x-1); y=trans(y-1); 66 bigsta+=bin[x*3+y]; 67 } 68 if(dfs(bigsta)) printf("Yes\n"); 69 else printf("No\n"); 70 } 71 return 0; 72 }
