Fantasia (Tarjan+树形DP)
Time Limit: 1000 ms Memory Limit: 256 MB
Description
给定一张N个点、M条边的无向图 $G$ 。每个点有个权值Wi。
我们定义 $G_i$ 为图 $G$ 中删除第 $i$ 号顶点后的图。我们想计算 $G_1, G_2, ..., G_n$ 这N张图的权值。
对于任意一张图 $G$ ,它的权值是这样定义的:
1. 如果 $G$ 是联通图,那么 $G$ 的权值为 $G$ 中所有顶点权值的乘积。
2. 如果 $G$ 是非联通图,那么 $G$ 的权值为 $G$ 中所有联通块的权值之和。
$G$ 中的一个联通块指的是 $G$ 的一个子图,并且这个子图中的点两两相连(包括直接连接或者间接连接),并且不存在子图外的点使得子图内的点能与子图外的点相连。
Input
第一行包含两个整数 $n$ 和 $m$ $(2 \le n \le 10^5, 1 \le m \le 2 \times 10^5)$ ,分别表示点数和边数。
第二行包含 $n$ 个整数 $w_1, w_2, ..., w_n$ $(1 \le w_i \le 10^9)$, 表示每个顶点的权值。
接下来 m 行,每行两个整数 $x_i$ 和 $y_i$ $(1 \le x_i, y_i \le n, x_i \ne y_i)$, 表示一条无向边。
输出只有一个整数: $S = (\sum\limits_{i=1}^{n}i\cdot z_i) \text{ mod } (10^9 + 7)$, 其中 $z_i$ 是图 $G_i$ 的权值。
Sample Input |
Sample Output |
10 3
3 3 3
2 3 3
2 3 1
3 1 1
3 1 2
1 3 1
1 1 2
1 2 2
1 3 2
1 2 1
|
3
1
3
0
1
0
1
0
0
1
|
Hint
【数据范围及约定】
子任务1(5分): $n \leq 10, m \leq 20$
子任务2(10分): $n \leq 1000, m \leq 2000$
子任务3(20分): 该图恰为一棵树,$m = n-1$
子任务4(20分): 该图为一幅联通图
子任务5(45分): 我们会拿最强的数据来评测你的程序(mmp)
对于所有数据,$2 \le n \le 10^5, 1 \le m \le 2 \times 10^5$
题解
没有什么能阻挡我把Tarjan打残。
题目涉及到删点操作。
如果删的点$u$是一个非割顶,那么它的消失貌似对这个联通块整体没有太大的影响,要处理的话仅仅是该当前联通块的权值$val$除去$u$的权值$w_u$。
如果删的点$u$是一个割顶,那么它会将这个联通块分成若干部分,具体就是在Tarjan的缩点树上,把子树全部断开,把父亲也断开。问题来了,割顶这个东西很烦怎么处理?
转树
割顶出现了!它可以同时处于多个点双内,mmp
对于每个点双,我们暂且新建一个代表点,将点双内的所有点连向这个代表点。这样,一个割顶可以被连接到多个点双的代表点,同时整个图转成了树的形态。
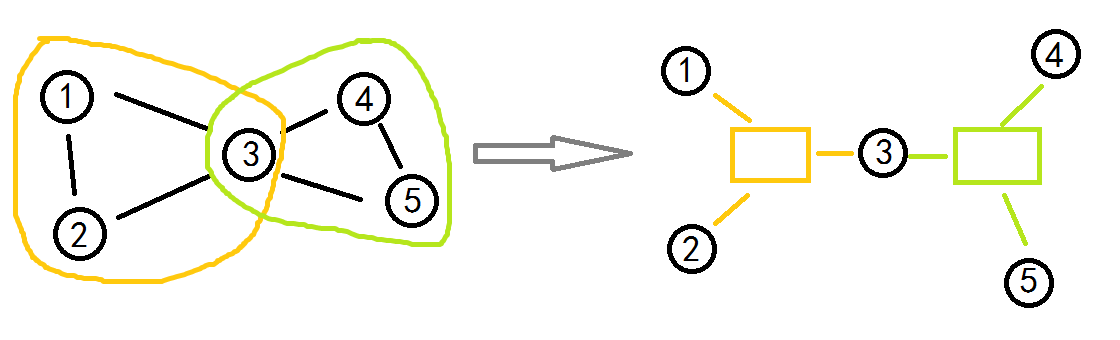
那么断开一个割顶$u$会影响到哪些区块,就一目了然了,即这种树上,$u$的所有子树和父亲那一头的部分。
发现这其实同化了断开非割顶的操作,非割顶永远处于根节点或叶子节点,其实本质上处理是一样的。
维护
$$f_u=\prod\limits_{v\in 以u为根的树}w[v]\\g_u=\sum\limits_{v是u的子树}f[v]$$
则删去一个点$u$,对所在联通块权值$val$的影响即为:
$$val=\frac{val}{f_u}+g_u$$
即父亲那一头的权值+所有子树的权值和
小细节与特判
1.处理删去割顶的时候(即上面的最后一个公式),$\frac{val}{f_u}$希望得到的是父亲那一头的权值,但如果$u$是树的根,这玩意弄出来却是1,而不是我们希望的0(坑爹),所以记录一下我们要处理的割顶是不是一个树的根,特判一下。
2.Tarjan深搜的起始点要记为割顶。

1 #include <cstdio> 2 #define min(a,b) (a<b?a:b) 3 using namespace std; 4 typedef long long ll; 5 const ll N=200010,Mod=1e9+7; 6 int n,m,h1[N],h2[N*2],tot; 7 int col[N],colcnt,st[N],top,bcnt,head[N]; 8 ll info[N],sumup,ans,f[N*2],g[N*2],w[N*2]; 9 int dfn[N],low[N],ins[N],tmcnt; 10 bool cut[N]; 11 struct Edge{int v,next;}G[N*6]; 12 inline void addEdge(int u,int v,int *h){ 13 G[++tot].v=v; G[tot].next=h[u]; h[u]=tot; 14 } 15 void tarjan(int u,int fa){ 16 st[++top]=u; 17 ins[u]=1; 18 dfn[u]=low[u]=++tmcnt; 19 col[u]=colcnt; 20 info[col[u]]=(info[col[u]]*w[u])%Mod; 21 for(int i=h1[u],v,ccnt=0;i;i=G[i].next) 22 if((v=G[i].v)!=fa){ 23 if(!ins[v]){ 24 ccnt++; 25 tarjan(v,u); 26 low[u]=min(low[u],low[v]); 27 if((!fa&&ccnt>1)||(fa&&dfn[u]<=low[v])) 28 cut[u]=1; 29 if(dfn[u]<=low[v]){ 30 w[(++bcnt)+n]=1; 31 do{ 32 addEdge(st[top],bcnt+n,h2); 33 addEdge(bcnt+n,st[top],h2); 34 top--; 35 }while(st[top+1]!=v); 36 addEdge(u,bcnt+n,h2); 37 addEdge(bcnt+n,u,h2); 38 } 39 } 40 else if(ins[v]==1) 41 low[u]=min(low[u],dfn[v]); 42 } 43 ins[u]=2; 44 } 45 void dfs(int u,int fa){ 46 f[u]=w[u]; g[u]=0; 47 for(int i=h2[u],v;i;i=G[i].next) 48 if((v=G[i].v)!=fa){ 49 dfs(v,u); 50 f[u]=(f[u]*f[v])%Mod; 51 g[u]=(g[u]+f[v])%Mod; 52 } 53 } 54 ll ksm(ll bas,ll tm){ 55 if(tm==0) return 1; 56 ll ret=ksm(bas,tm/2); 57 ret=(ret*ret)%Mod; 58 return ((tm&1)?ret*bas:ret)%Mod; 59 } 60 ll inv(int x){return ksm(x,Mod-2);} 61 int main(){ 62 scanf("%d%d",&n,&m); 63 for(int i=1;i<=n;i++) scanf("%lld",&w[i]); 64 for(int i=1,u,v;i<=m;i++){ 65 scanf("%d%d",&u,&v); 66 addEdge(u,v,h1); addEdge(v,u,h1); 67 } 68 for(int i=1;i<=n;i++) 69 if(!dfn[i]){ 70 info[++colcnt]=1; 71 tarjan(i,0); 72 cut[i]=1; 73 sumup=(sumup+info[colcnt])%Mod; 74 head[colcnt]=i; 75 dfs(i,0); 76 } 77 for(ll i=1,k;i<=n;i++){ 78 int c=col[i]; 79 if(!cut[i]) 80 k=(sumup+Mod*2-info[c]+(info[c]*inv(w[i]))%Mod)%Mod; 81 else{ 82 if(head[c]!=i) k=(sumup+Mod*2-info[c]+(info[c]*inv((f[i])%Mod)%Mod)%Mod+g[i])%Mod; 83 else k=(sumup+Mod*2-info[c]+g[i])%Mod; 84 } 85 ans=(ans+(i*k)%Mod)%Mod; 86 } 87 printf("%lld\n",ans); 88 return 0; 89 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号