SLAM问题中滑动窗口边缘化

 SLAM问题中滑动窗口边缘化

本文参考作者文章：https://www.cnblogs.com/long5683/p/13563810.html

一、从高斯分布到信息矩阵

1.1 slam问题的引入与描述建模

一般情况下状态估计主要分为运动方程和观测方程，为了简便描述问题，本文只考虑简化的观测方程。

 

 1.2 slam问题求解

1.3 高斯分布和协方差矩阵

 

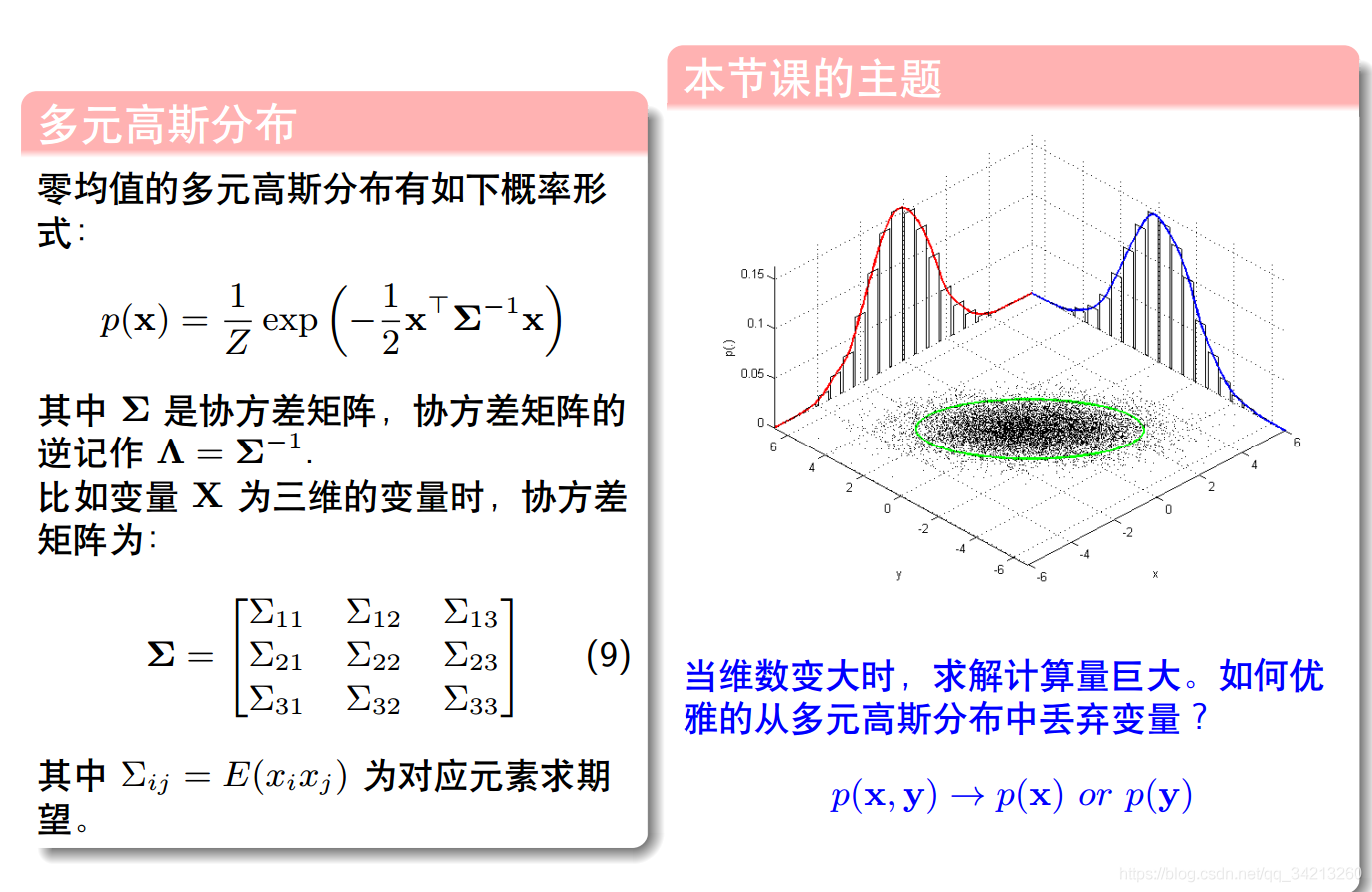
 1. 4实例

1.4.1实例1

 

 

求实例协方差矩阵

如果要从从实例中除去变量x3，类似滑动窗口

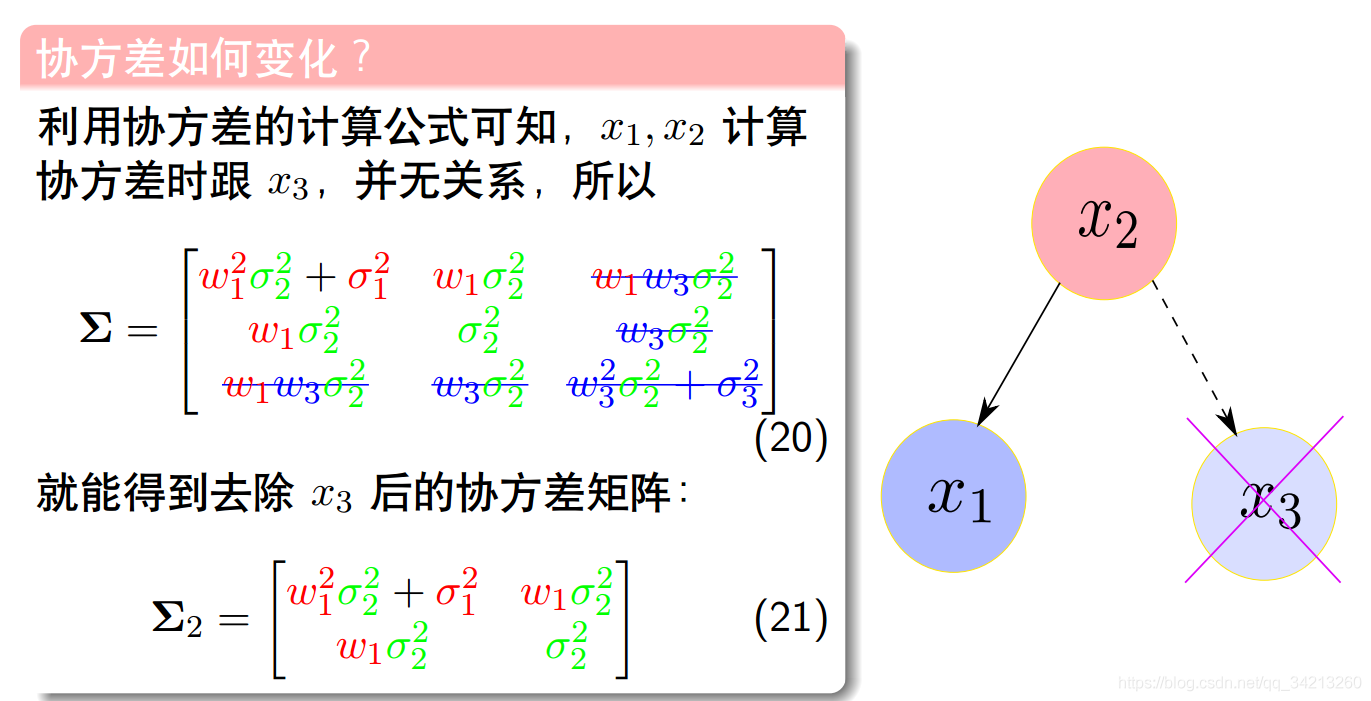
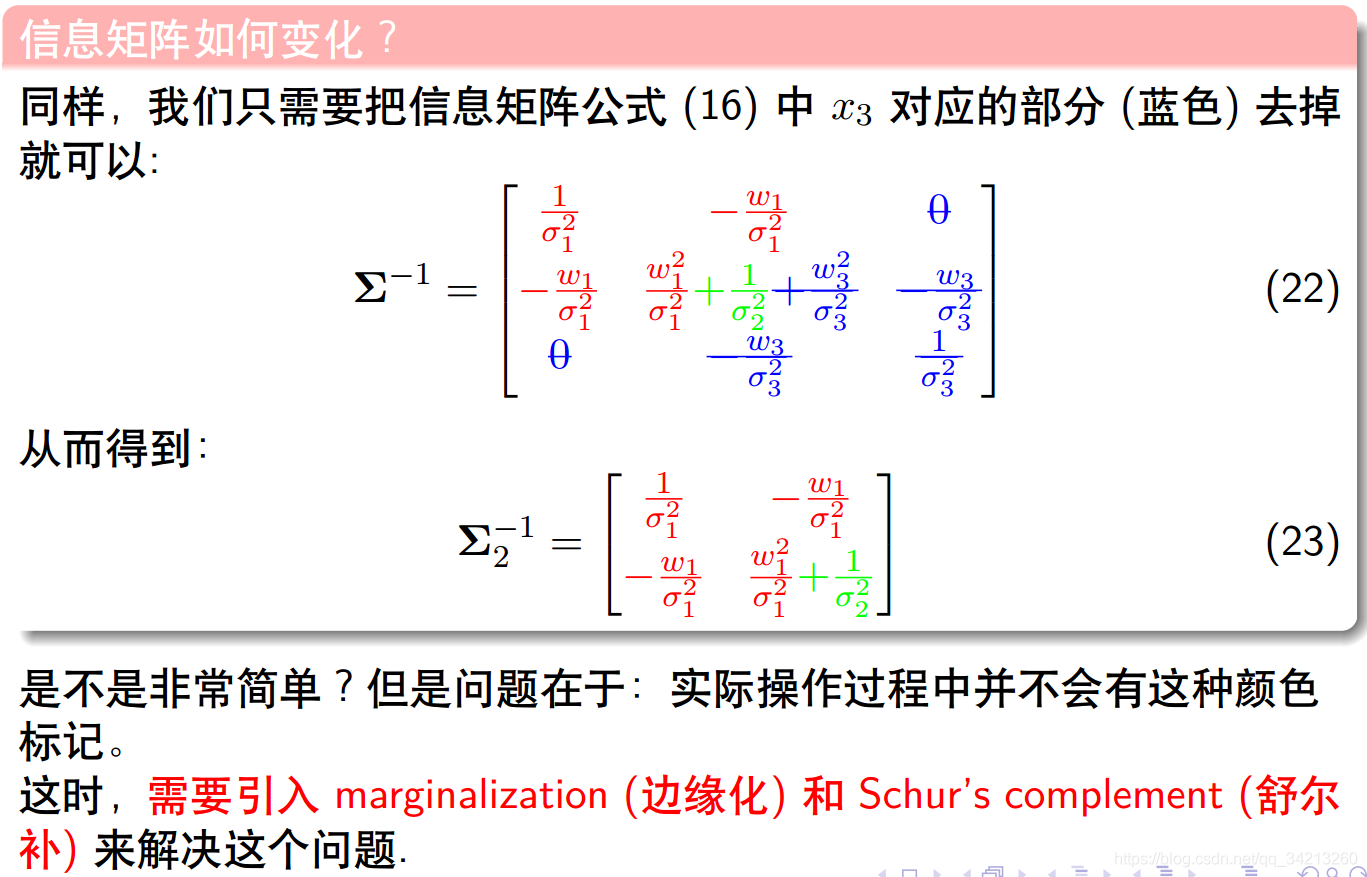
1.4.1实例2

二、舒尔补应用：边际概率, 条件概率

 

2.1舒尔补概念

2.2 舒尔补由来

同理舒尔补还可以写成另一种形式

 

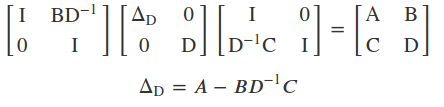
2.3 使用舒尔补分解的好处

2.4 舒尔补应用于多元高斯分布

2.5 关于 P(a), P(b|a) 的协方差矩阵

2.6 关于 P(a), P(b|a) 的信息矩阵

2.7 回顾样例

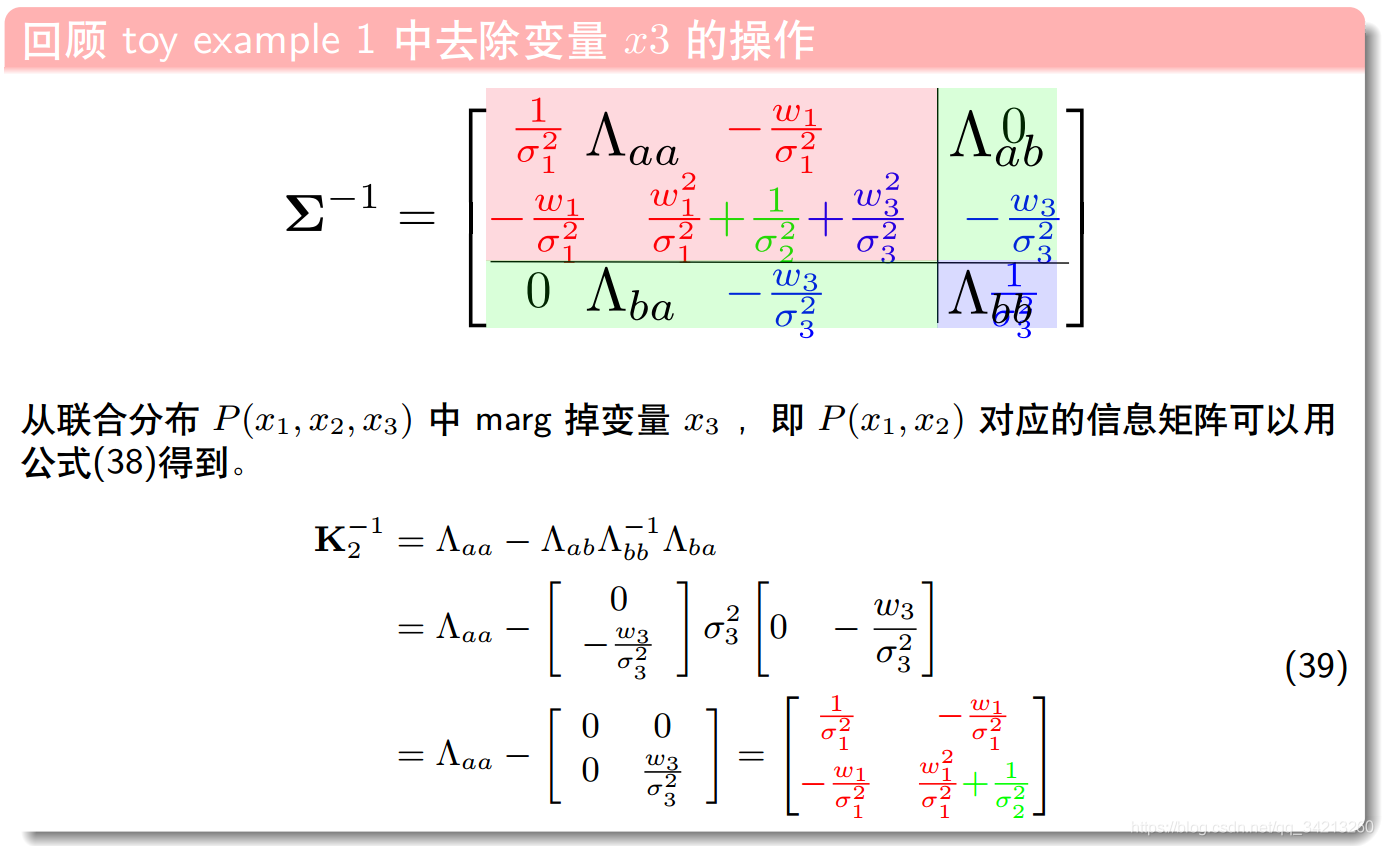
2.8 总结

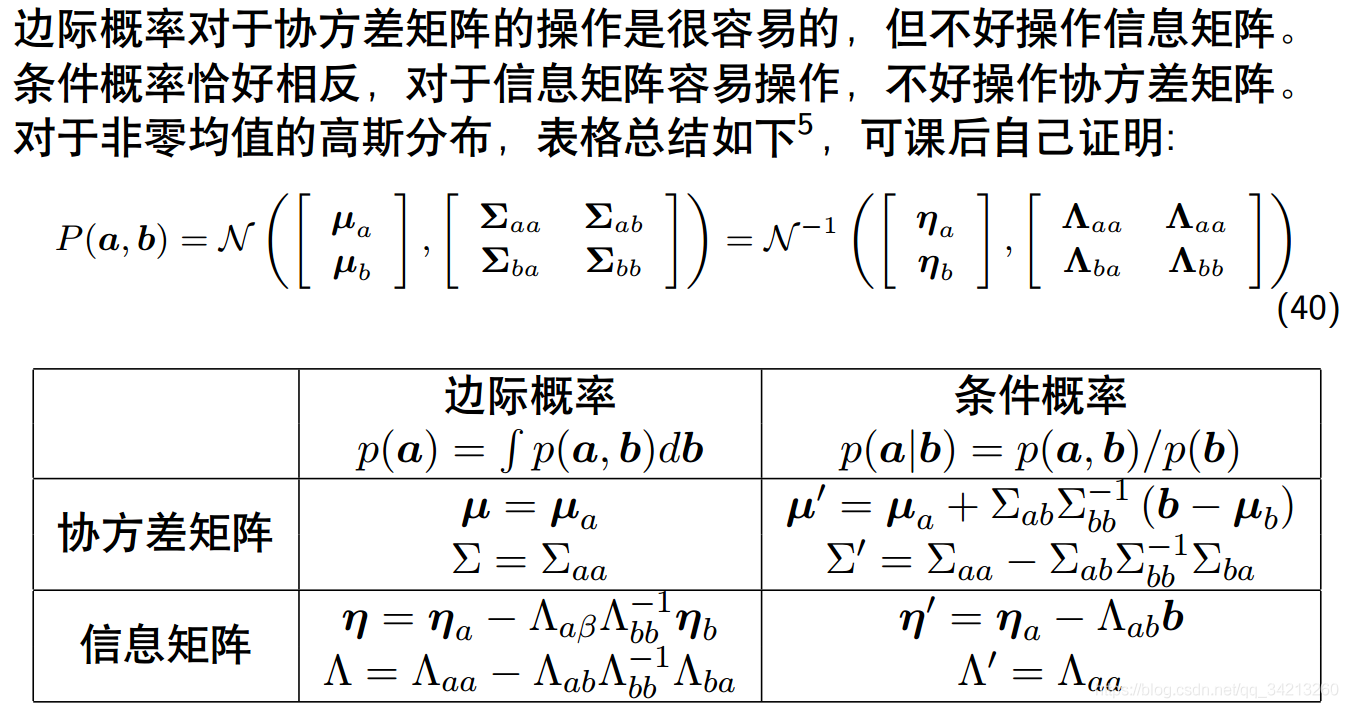
三、滑动窗口算法

3.1 最小二乘用图表示

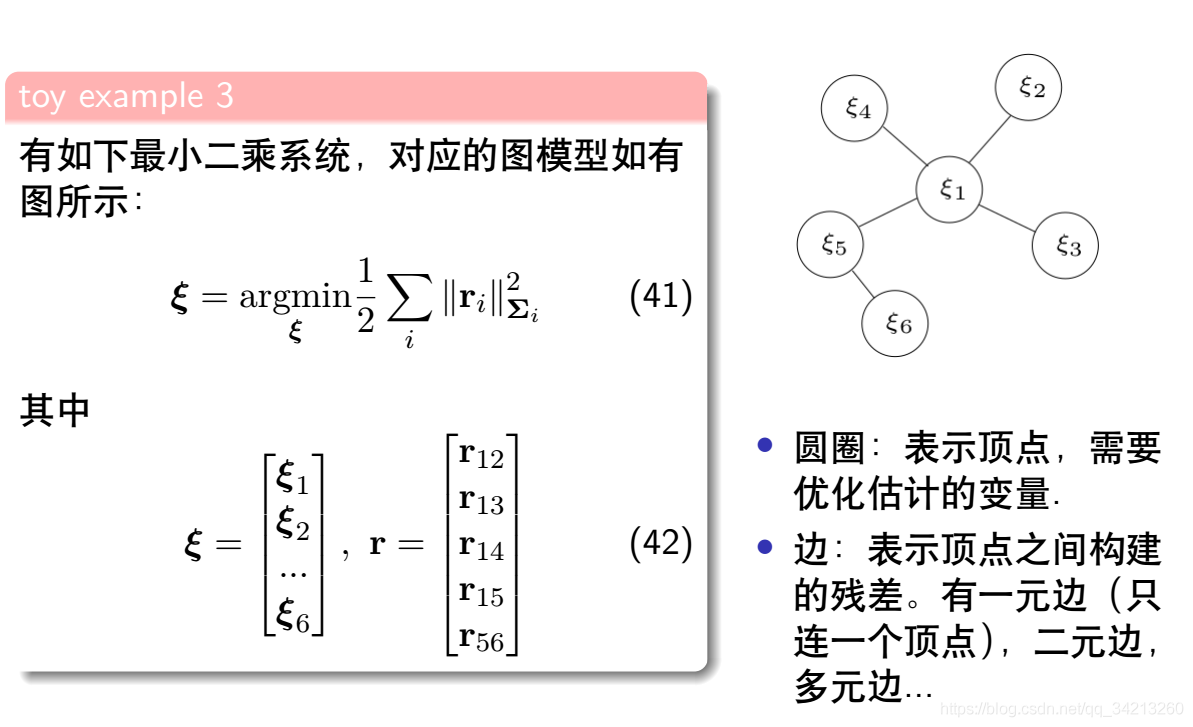
3.2 最小二乘问题信息矩阵的构成

3.3 信息矩阵的稀疏性

3.4 信息矩阵组装过程的可视化

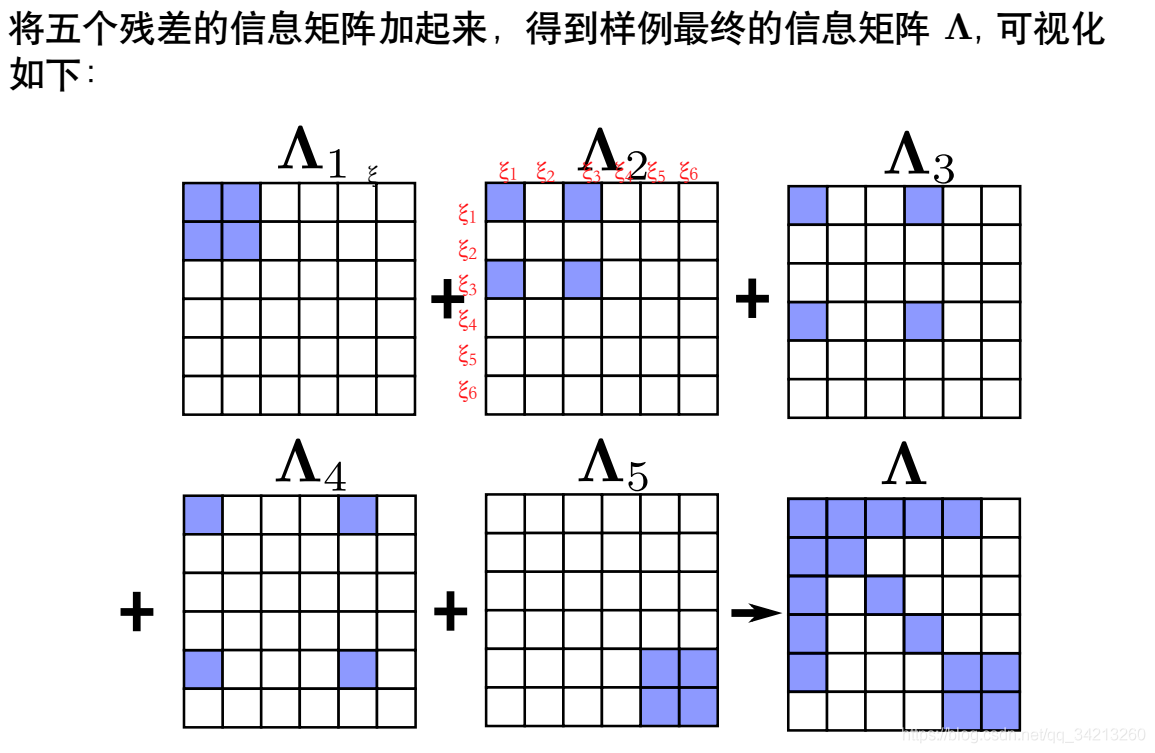
3.5 基于边际概率的滑动窗口算法

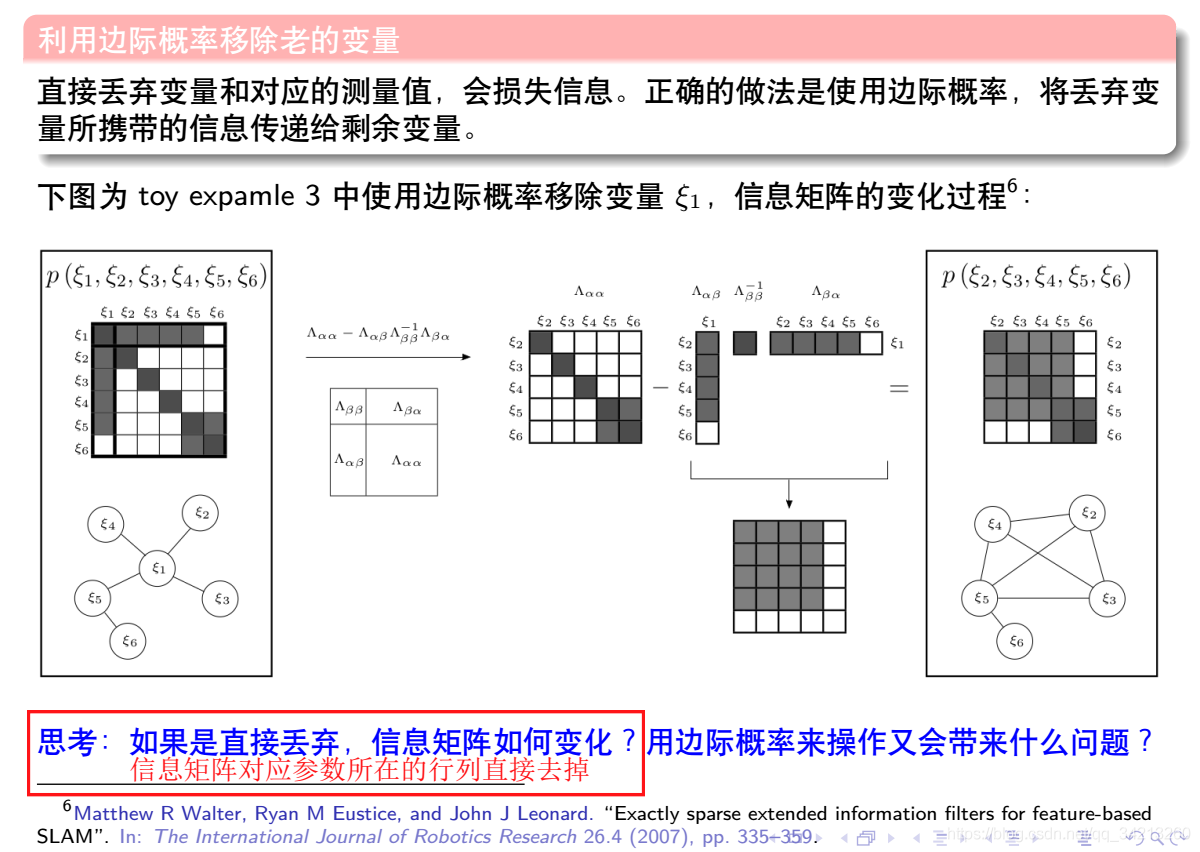
假设要被边缘化的状态是δx_a

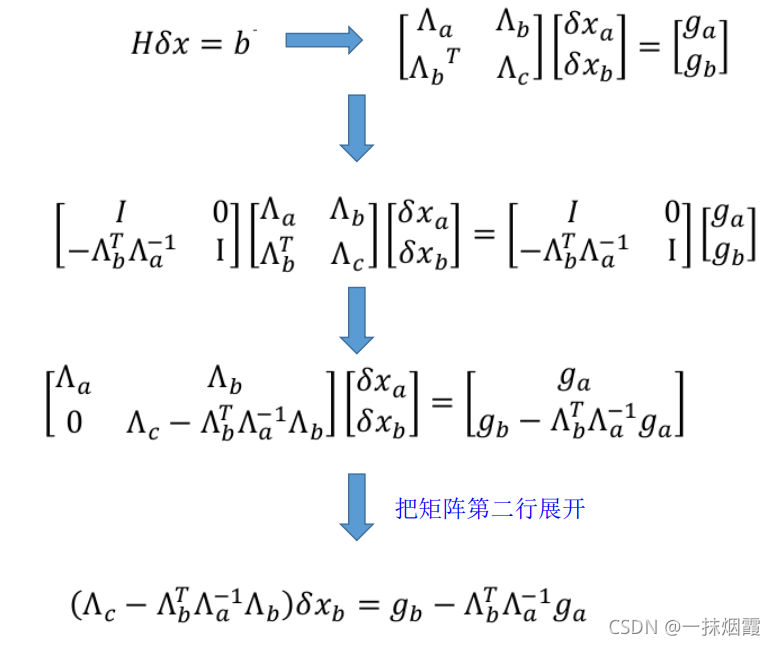
际滑窗中δx_a的状态已经被移出去了，所以不会再产生约束，所以只展开矩阵第二行_。

可以看到新的方程只和δx_b 相关，但是δx_a的信息又被保留了下来。接下来只需把最后的公式重写分解成以下形式就又形成了常见后端中的边缘化约束

3.6 样例

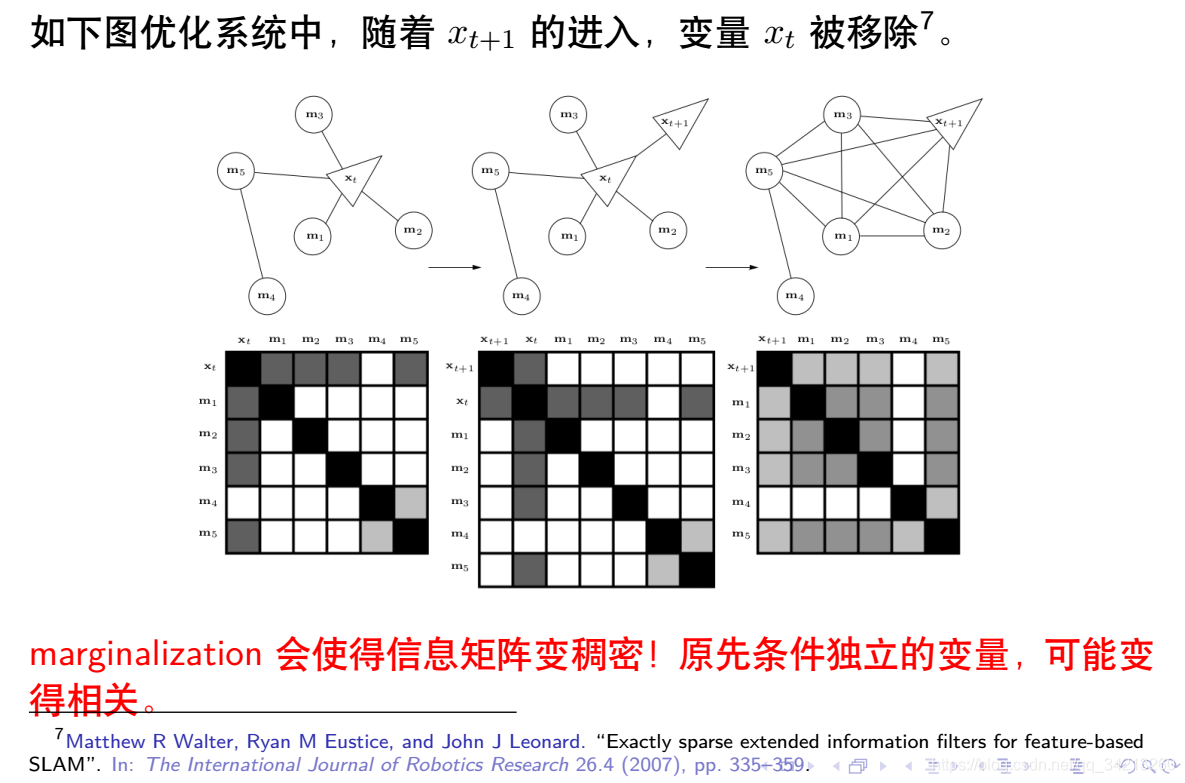
详细步骤如下：
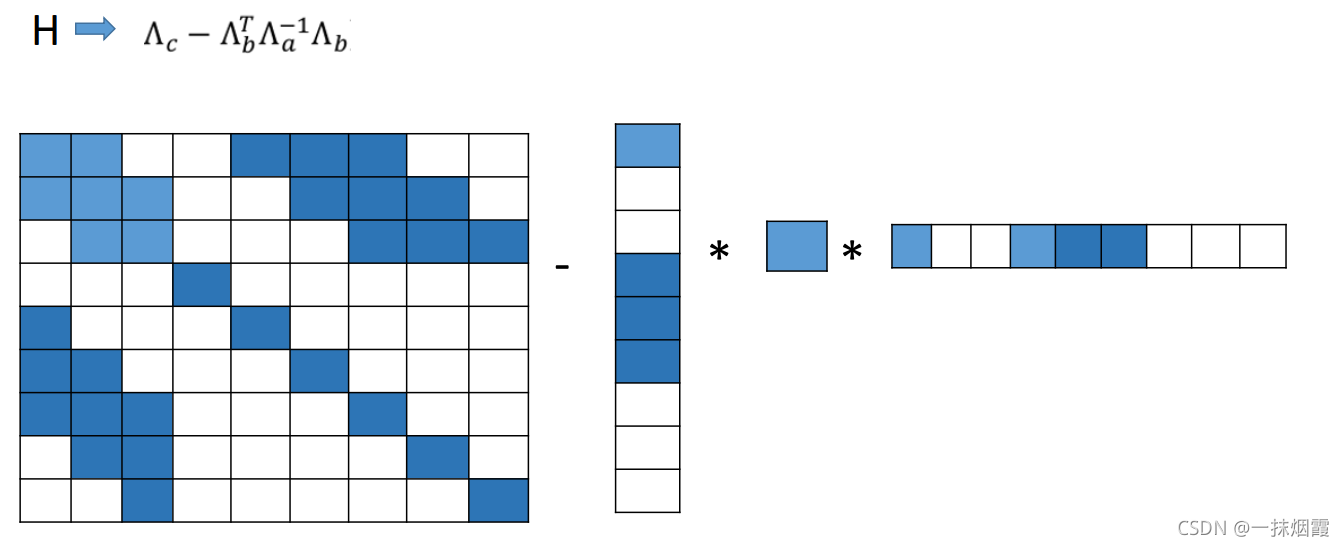
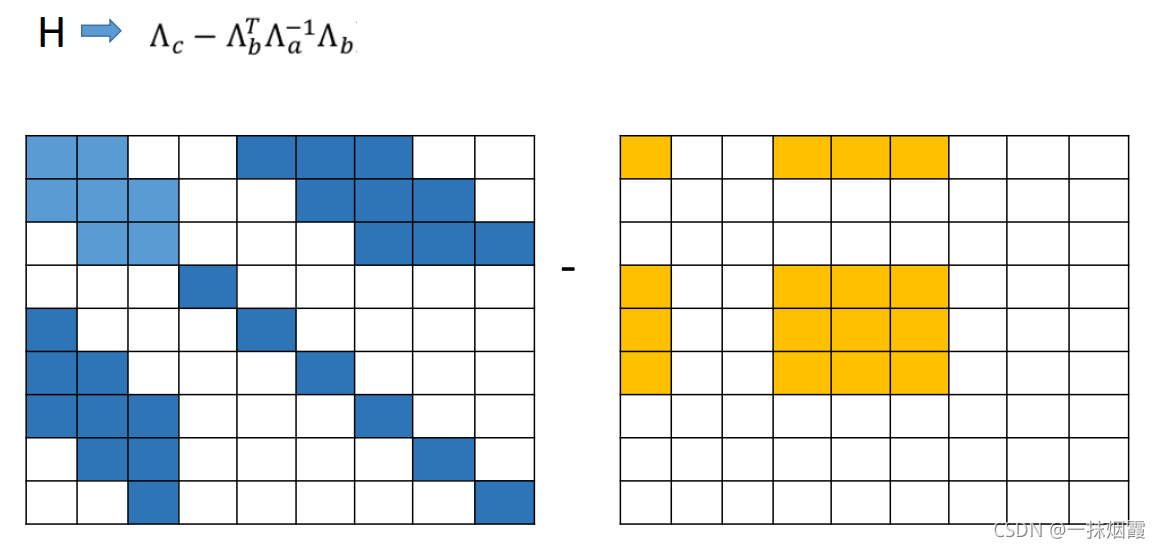
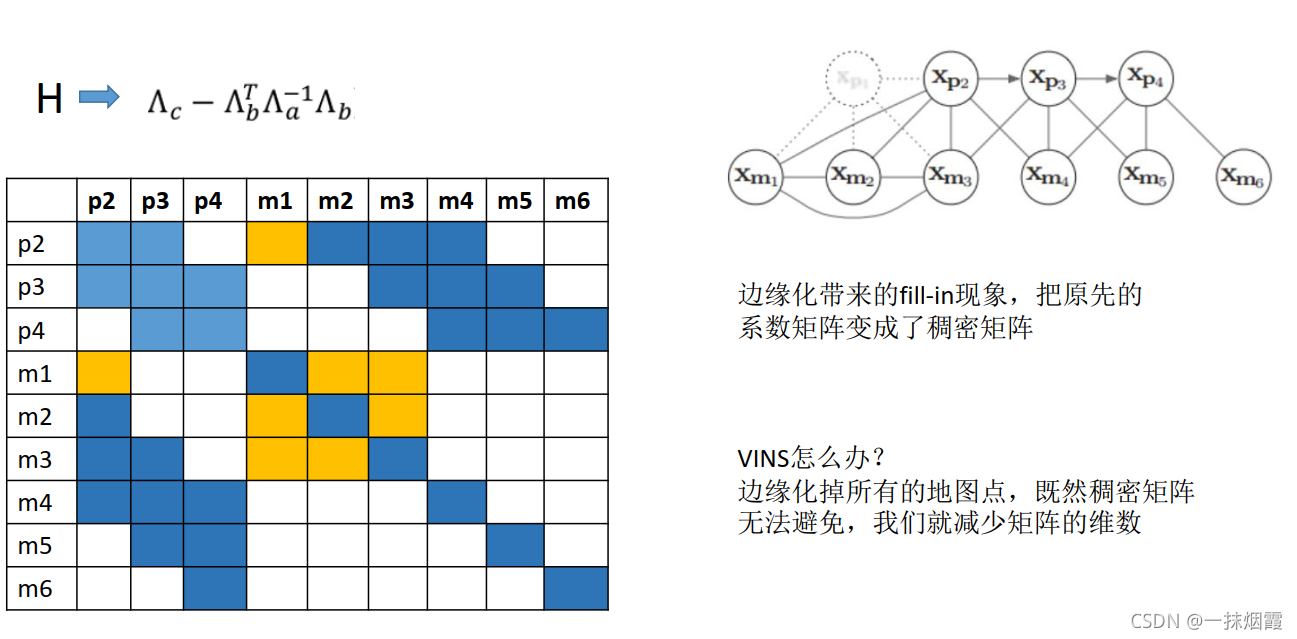
左边为因子图，右边为其对应的H矩阵

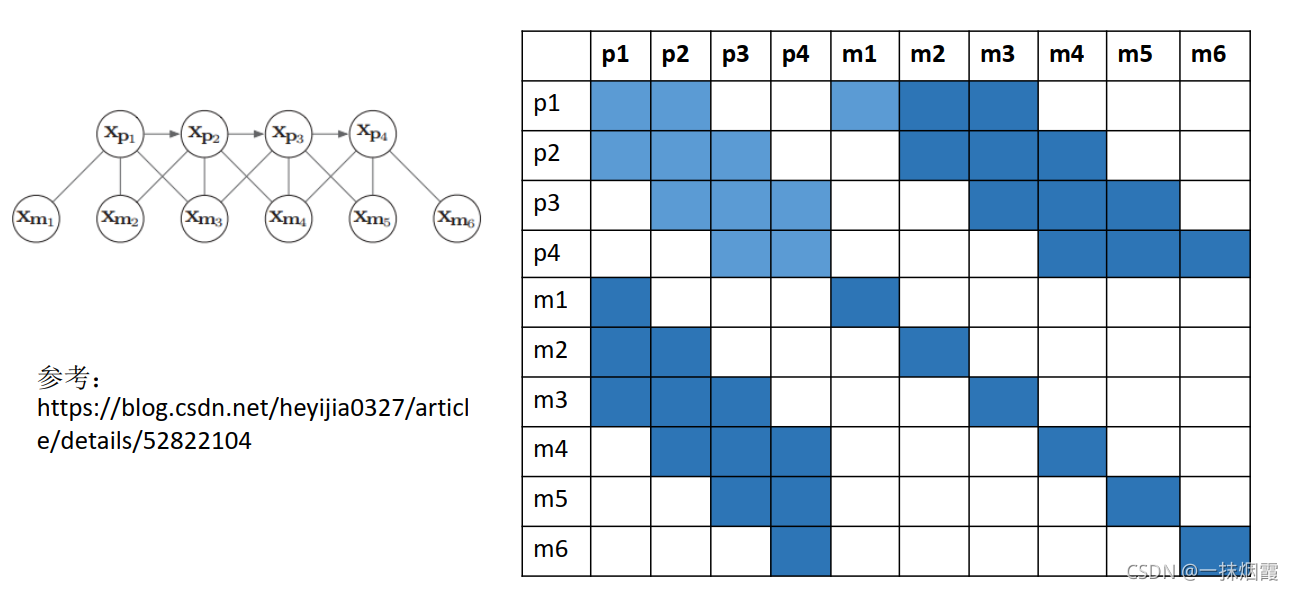
如果边缘化掉pose1会发生什么？

四、滑动窗口中的 FEJ 算法

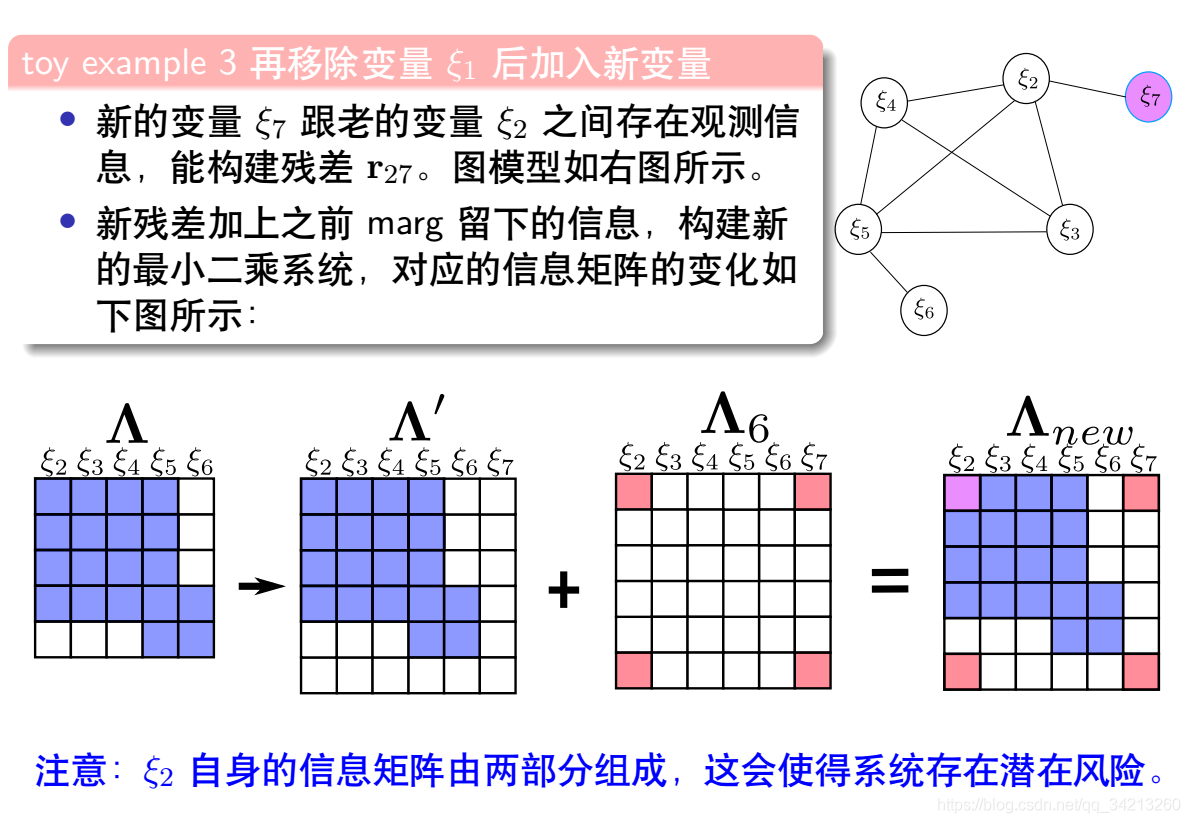
4.1 新测量信息和旧测量信息构建新的系统

4.2 信息矩阵的零空间变化

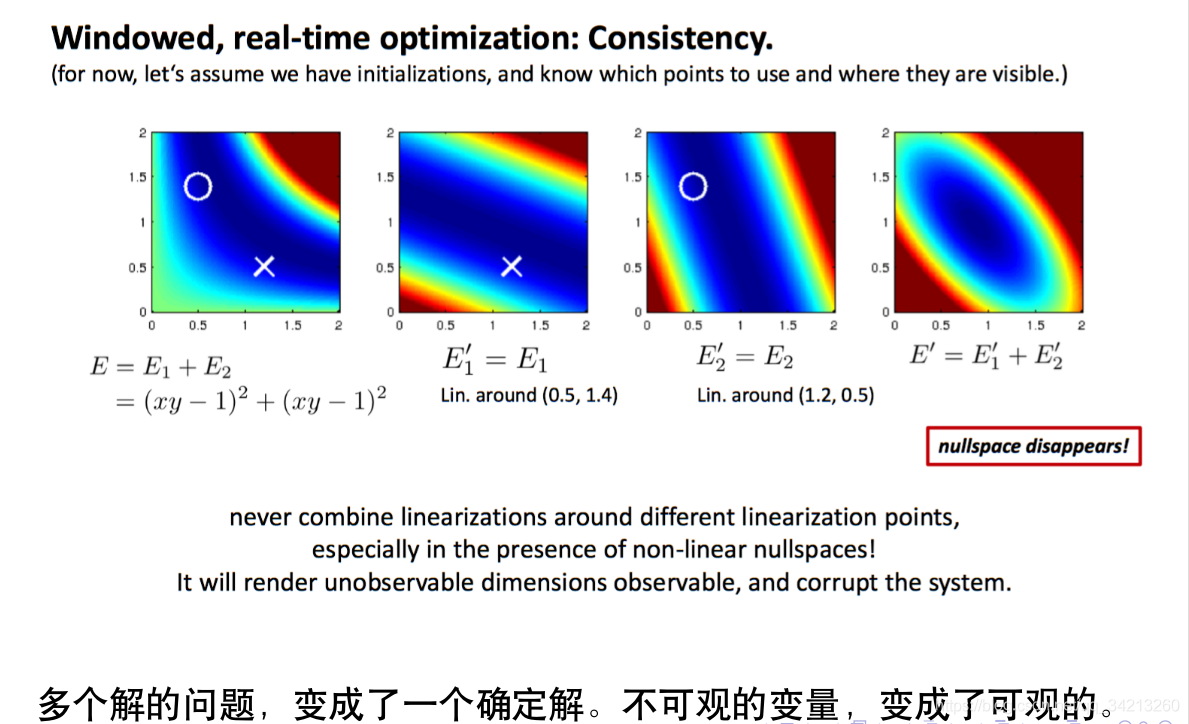
4.3 可观性的一种定义