强化学习-学习笔记14 | 策略梯度中的 Baseline

本篇笔记记录学习在 策略学习 中使用 Baseline，这样可以降低方差，让收敛更快。

14. 策略学习中的 Baseline

14.1 Baseline 推导

• 在策略学习中，我们使用策略网络 \(\pi(a|s;\theta)\) 控制 agent，

• 状态价值函数

  \(V_\pi(s)=\mathbb{E}_{A\sim \pi}[Q_\pi(s,A)]=\sum\limits_{a}\pi(a|s;\theta)\cdot Q_\pi(a,s)\)

• 策略梯度：

  \(\frac{\partial \ V_\pi(s)}{\partial \ \theta}=\mathbb{E}_{A\sim\pi}[\frac{\partial ln \pi(A|s;\theta)}{\partial \theta}\cdot Q_\pi(s,A)]\)

在策略梯度算法中引入 Baseline 主要是用于减小方差，从而加速收敛

Baseline 可以是任何 独立于 动作 A 的数，记为 b。

Baseline的性质：

• 这个期望是0： \(\mathbb{E}_{A\sim\pi}[b\cdot \frac{\partial \ \ln\pi(A|s;\theta)}{\partial\theta}]=0\)

  • 因为 b 不依赖 动作 A ，而该式是对 A 求期望，所以可以把 b 提出来，有：\(b\cdot \mathbb{E}_{A\sim\pi}[\frac{\partial \ \ln\pi(A|s;\theta)}{\partial\theta}]\)

  • 而期望 E 这一项可以展开：\(b\sum_a \pi(a|s;\theta)\cdot\frac{\partial\ln_\pi(A|s;\theta)}{\partial\theta}\)

    这个性质在策略梯度算法用到的的两种形式有提到过。

  • 用链式法则展开后面的导数项，即: \(\frac{\partial\ln_\pi(A|s;\theta)}{\partial\theta}={\frac{1}{\pi(a|s;\theta)}\cdot \frac{\partial\pi(a|s;\theta)}{\partial\theta}}\)

  • 这样整个式子为：\(b\sum_a \pi(a|s;\theta)\cdot{\frac{1}{\pi(a|s;\theta)}\cdot \frac{\partial\pi(a|s;\theta)}{\partial\theta}}=b\cdot \sum_a\frac{\partial\pi(a|s;\theta)}{\partial\theta}\)

  • 由于连加是对于 a 进行连加，而内部求导是对于 θ 进行求导，所以求和符号可以和导数符号交换位置：

    \(b\cdot \frac{\partial\sum_a\pi(a|s;\theta)}{\partial\theta}\)

    这是数学分析中 级数部分 的内容。

  • 而 \(\sum_a\pi(a|s;\theta)=1\)，所以有\(b\cdot \frac{\partial 1}{\partial \theta}=0\)

根据上面这个式子的性质，可以向 策略梯度中添加 baseline

• 策略梯度 with baseline：$$\frac{\partial \ V_\pi(s)}{\partial \ \theta}=\mathbb{E}{A\sim\pi}[\frac{\partial ln \pi(A|s;\theta)}{\partial \theta}\cdot Q\pi(s,A)]- \mathbb{E}{A\sim\pi}[b\cdot \frac{\partial \ \ln\pi(A|s;\theta)}{\partial\theta}] \=\mathbb{E}[\frac{\partial ln \pi(A|s;\theta)}{\partial \theta}\cdot(Q_\pi(s,A)-b)]$$
• 这样引入b对期望 \(\mathbb{E}\) 没有影响，为什么要引入 b 呢？
  • 策略梯度算法中使用的并不是 严格的上述式子，而是它的蒙特卡洛近似；
  • b不影响期望，但是影响蒙特卡洛近似；
  • 如果 b 好，接近 \(Q_\pi\)，那么会让蒙特卡洛近似的方差更小，收敛速度更快。

14.2 策略梯度的蒙特卡洛近似

上面我们得到：\(\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}=\mathbb{E}_{A_t\sim\pi}[\frac{\partial ln \pi(A_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,A_t)-b)]\)

但直接求期望往往很困难，通常用蒙特卡洛近似期望。

• 令 \(g(A_t)=[\frac{\partial ln \pi(A_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,A_t)-b)]\)

• 根据策略函数 \(\pi\) 随机抽样 \(a_t\) ，计算 \(g(a_t)\)，这就是上面期望的蒙特卡洛近似；\(g(a_t)=[\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,a_t)-b)]\)

• \(g(a_t)\) 是对策略梯度的无偏估计；

  因为：\(\mathbb{E}_{A_t\sim\pi}[g(A_t)]=\frac{\partial V_\pi(s_t)}{\partial\theta}\)，期望相等。

• \(g(a_t)\) 是个随机梯度，是对策略梯度 \(\mathbb{E}_{A_t\sim\pi}[g(A_t)]\)的蒙特卡洛近似

• 在实际训练策略网络的时候，用随机梯度上升更新参数θ：\(\theta \leftarrow \theta+\beta\cdot g(a_t)\)

• 策略梯度是 \(g(a_t)\) 的期望，不论 b 是什么，只要与 A 无关，就都不会影响 \(g(A_t)\) 的期望。为什么不影响已经在 14.1 中讲过了。

  • 但是 b 会影响 \(g(a_t)\)；
  • 如果 b 选取的很好，很接近 \(Q_\pi\)，那么随机策略梯度\(g(a_t)\)的方差就会小；

14.3 Baseline的选取

介绍两种常用的 baseline。

a. b=0

第一种就是把 baseline 取0，即与之前相同：\(\frac{\partial \ V_\pi(s)}{\partial \ \theta}=\mathbb{E}_{A\sim\pi}[\frac{\partial ln \pi(A|s;\theta)}{\partial \theta}\cdot Q_\pi(s,A)]\)

b. b= \(V_\pi\)

另一种就是取 b 为 \(V_\pi\)，而 \(V_\pi\) 只依赖于当前状态 \(s_t\)，所以可以用来作为 b。并且 \(V_\pi\) 很接近 \(Q_\pi\)，可以降低方差加速收敛。

因为 \(V_\pi(s_t)=\mathbb{E}[Q_\pi(s_t,A_t)]\)，作为期望，V 很接近 Q。

14.4 Reinforce with Baseline

把 baseline 用于 Reinforce 算法上。

a. 基本概念

• 折扣回报：\(U_t=R_t+\gamma\cdot R_{t+1}+\gamma^2\cdot R_{t+2}+...\)

• 动作价值函数：\(Q_\pi(s_t,a_t)=\mathbb{E}[U_t|s_t,a_t].\)

• 状态价值函数：\(V_\pi(s_t)=\mathbb{E}_A[Q_\pi(s_t,A)|s_t]\)

• 应用 baseline 的策略梯度：使用的是上面第二种 baseline：

  \(\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}=\mathbb{E}_{A_t\sim\pi}[g(A_t)]=\mathbb{E}_{A_t\sim\pi}[\frac{\partial ln \pi(A_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,A_t)-V_\pi(s_t))]\)

• 对动作进行抽样，用 \(g(a_t)\) 做蒙特卡洛近似，为无偏估计（因为期望==策略梯度）：\(a_t\sim\pi(\cdot|s_t;\theta)\)

  \(g(a_t)\) 就叫做 随机策略梯度，用随机抽取的动作 对应的值来代替期望，是策略梯度的随即近似；这正是蒙特卡洛方法的应用。

  • \(g(a_t)=[\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,a_t)-b)]\)

但上述公式中还是有不确定的项:\(Q_\pi \ \ V_\pi\)，继续近似：

• 用观测到的 \(u_t\) 近似 \(Q_\pi\)，因为 \(Q_\pi(s_t,a_t)=\mathbb{E}[U_t|s_t,a_t].\)这也是一次蒙特卡洛近似。

  这也是 Reinforce 算法的关键。

• 用神经网络-价值网络 \(v(s;w)\) 近似 \(V_\pi\)；

所以最终近似出来的 策略梯度 是：

\[\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}\approx g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(u_t-v(s;w)) \]

当我们知道 策略网络\(\pi\)、折扣回报\(u_t\) 以及 价值网络\(v\)，就可以计算这个策略梯度。

我们总计做了3次近似：

1. 用一个抽样动作 \(a_t\) 带入 \(g(a_t)\) 来近似期望；

2. 用回报 \(u_t\) 近似动作价值函数\(Q_\pi\)；

   1、2都是蒙特卡洛近似；

3. 用神经网络近似状态价值函数\(V_\pi\)

   函数近似。

b. 算法过程

我们需要建立一个策略网络和一个价值网络，后者辅助训练前者。

• 策略网络：

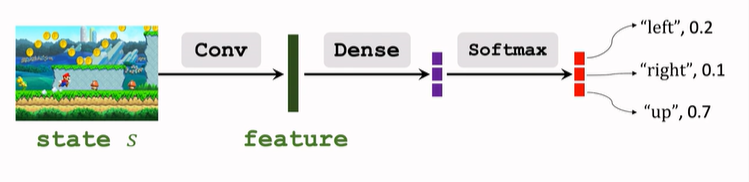
• 价值网络：

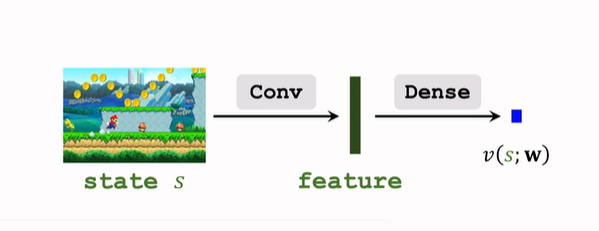
• 参数共享：

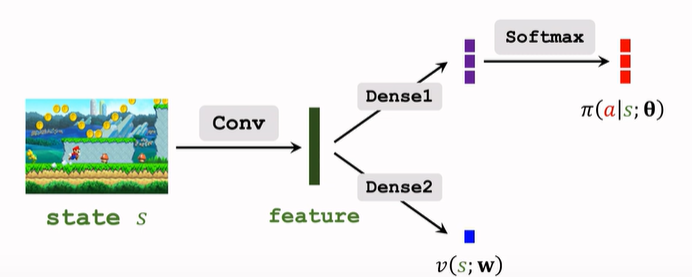
用 Reinforce 算法训练策略网络，用回归方法训练价值网络。

• 在一次训练中 agent 获得轨迹：\(s_1,a_1,r_1,s_2,a_2,r_2,...\)

• 计算 \(u_t=\sum_{i=t}^n\gamma^{i-t}r^i\)

• 更新策略网络

  1. 得到策略梯度：\(\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(u_t-v(s;w))\)

  2. 梯度上升，更新参数：\(\theta\leftarrow \theta + \beta\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial\theta}\cdot(u_t-v(s_t;w))\)

     记 \(u_t-v(s_t;w)\) 为 \(-\delta_t\)

     \(\theta\leftarrow \theta - \beta\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial\theta}\cdot \delta_t\)

• 更新价值网络

  回顾一下价值网络的目标：\(V_\pi\) 是 \(U_t\) 的期望，训练价值网络是让v接近期望 \(V_\pi\)

  1. 用观测到的 \(u_t\) 拟合 v，两者之间的误差记为

     prediction error:\(\delta_t=v(s_t;w)-u_t\)，

  2. 求导得策略梯度: \(\frac{\partial \delta^2/2}{\partial w}=\delta_t\cdot \frac{\partial v(s_t;w)}{\partial w}\)

  3. 梯度下降更新参数：\(w\leftarrow w-\alpha\cdot\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}\)

• 如果轨迹的长度为n，可以对神经网络进行n次更新

14.5 A2C算法

a.基本概念

Advantage Actor Critic. 把 baseline 用于 Actor-Critic 上。

所以需要一个策略网络 actor 和一个价值网络 critic。但与 第四篇笔记AC算法有所不同。

• 策略网络还是 \(\pi(a|s;\theta)\)，而价值网络是 \(v(s;w)\)，是对\(V_\pi\) 的近似，而不是第四篇笔记中的 \(Q_\pi\)。

  因为 V 不依赖于动作，而 Q 依赖动作和状态，故 近似V 的方法可以引入 baseline。

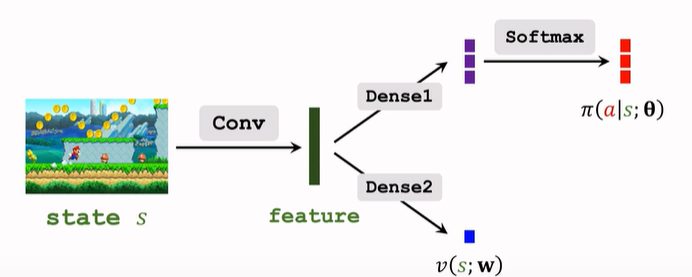
• A2C 网络结构：

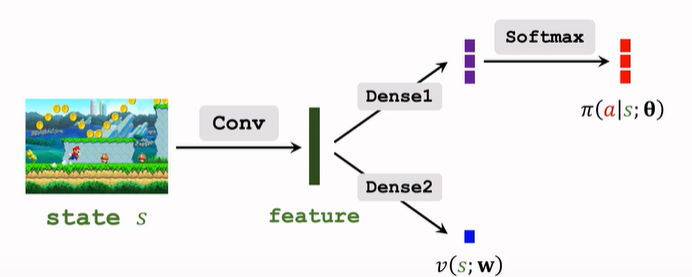
与 14.4 中的结构相同，区别在于训练方法不同。

b. 训练过程

1. 观察到一个 transition(\(s_t，a_t,r_t,s_{t+1}\))

2. 计算 TD target：\(y_t=r_t+\gamma\cdot v(s_{t+1};w)\)

3. 计算 TD error：\(\delta_t=v(s_t;w)-y_t\)

4. 用策略网络梯度更新策略网络θ：\(\theta\leftarrow \theta-\beta\cdot\delta_t\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial \theta}\)

   注意！这里的 \(\delta_t\)​ 是前文中的 “\(u_t-v(s_t;w)\) 为 \(-\delta_t\)”

5. 用TD更新价值网络：\(w\leftarrow w-\alpha\cdot\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}\)

c. 数学推导

A2C的基本过程就在上面，很简洁，下面进行数学推导。

1.价值函数的性质

• \(Q_\pi\)

  • TD算法推导时用到过这个式子：\(Q_\pi(s_t,a_t)=\mathbb{E}_{S_{t+1},A_{t+1}}[R_t+\gamma\cdot Q_\pi(S_{t+1},A_{t+1})]\)

  • 随机性来自 \(S_{t+1},A_{t+1}\)，而对之求期望正好消掉了随机性，可以把对 \(A_{t+1}\) 的期望放入括号内，\(R_t\) 与 \(A_{t+1}\) 无关，则有 定理一：

    \(Q_\pi(s_t,a_t)= \mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot \mathbb{E}_{A_{t+1}}[Q_\pi(S_{t+1},A_{t+1})]\\=\mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot V_\pi(s_{t+1})]\)

  • 即：\(Q_\pi(s_t,a_t)=\mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot V_\pi(s_{t+1})]\)

• \(V_\pi\)

  • 根据定义： \(V_\pi(s_t)=\mathbb{E}[Q_\pi(s_t,A_t)]\)

  • 将 Q 用 定理一 替换掉：

    \[V_\pi(s_t)=\mathbb{E}_{A_t}\mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot V_\pi(S_{t+1})]\\=\mathbb{E}_{A_t,S_{t+1}}[R_t+\gamma\cdot V_\pi(S_{t+1})] \]

  • 这就是 定理二：\(V_\pi(s_t)=\mathbb{E}_{A_t,S_{t+1}}[R_t+\gamma\cdot V_\pi(S_{t+1})]\)

这样就将 Q 和 V 表示为期望的形式，A2C会用到这两个期望，期望不好求，我们是用蒙特卡洛来近似求期望：

• 观测到 transition(\(s_t,a_t,r_t,s_{t+1}\))

• \(Q_\pi\)

  • \(Q_\pi(s_t,a_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})\)
  • 训练策略网络；

• \(V_\pi\)

  • \(V_\pi(s_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})\)
  • 训练价值网络，这也是TD target 的来源；

2. 更新策略网络

即使用 baseline 的策略梯度算法。

• \(g(a_t)=[\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,a_t)-V_\pi(s_t))]\) 是策略梯度的蒙特卡洛近似。

• 前面Dueling Network提到过，\(Q_\pi-V_\pi\)是优势函数 Advantage Function.

  这也是 A2C 的名字来源。

• Q 和 V 都还不知道，需要做近似，14.5.c.1 中介绍了：

  • \(Q_\pi(s_t,a_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})\)
  • 所以是：\(g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot[(r_t+\gamma\cdot V_\pi(s_{t+1}))-V_\pi(s_t)]\)
  • 对 \(V_\pi\) 进行函数近似 \(v(s;w)\)
  • 则得最终：\(g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot[(r_t+\gamma\cdot v(s_{t+1;w}))-v(s_{t;w})]\)

  用上式更新策略网络。

• 而 \(r_t+\gamma\cdot v(s_{t+1;w})\) 正是 TD target \(y_t\)

• 梯度上升更新参数：\(\theta\leftarrow \theta-\beta\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial \theta}\cdot (y_t-v(s_t;w))\)

  这样的梯度上升更好。

因为以上式子中都有 V，所以需要近似计算 V：

\(g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot\underbrace{[(r_t+\gamma\cdot V_\pi(s_{t+1}))-V_\pi(s_t)]}_{evaluation \ made \ by \ the \ critic}\)

3. 更新价值网络

采用 TD 算法 更新价值网络，根据 14.5.b 有如下式子：

• \(V_\pi(s_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})\)
• 对上式得 \(V_\pi\) 做函数近似， 替换为 \(v(s_t;w),v(s_{t+1;w})\)；
• \(v(s_t;w)\approx \underbrace{r_t+\gamma\cdot v(s_{t+1};w)}_{TD \ target \ y_t}\)
• 训练价值网络就是要让 \(v(s;w)\) 接近 \(y_t\)
  • TD error: \(\delta_t=v(s_t;w)-y_t\)
  • 梯度: \(\frac{\partial\delta^2_t/2}{\partial w}=\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}\)
  • 更新：\(w\leftarrow w-\alpha\cdot\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}\)

4. 有关的策略梯度

在A2C 算法中的策略梯度：\(g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot[(r_t+\gamma\cdot v(s_{t+1;w}))-v(s_{t;w})]\)

会有这么一个问题，后面这一项是由价值网络给出对策略网络选出的动作进行打分，那么为什么这一项中没有动作呢，没有动作怎么给动作打分呢？

• 注意这两项：
• \((r_t+\gamma\cdot v(s_{t+1;w}))\) 是执行完 \(a_t\) 后作出的预测
• \(v(s_t;w)\) 是未执行 \(a_t\) 时作出的预测；
• 两者之差意味着动作 \(a_t\) 对于 V 的影响程度
• 而在AC算法中，价值网络给策略网络的是 q，而在A2C算法中， 价值网络给策略网络的就是上两式之差 advantage.

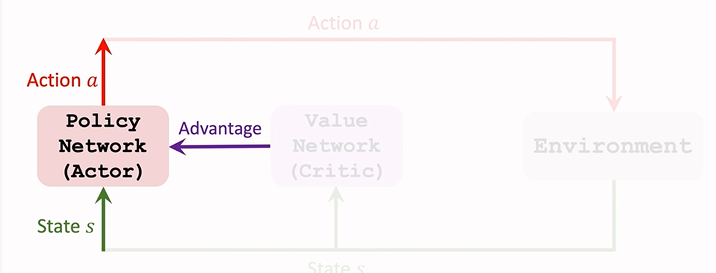
14.6 RwB 与A2C 的对比

• 两者的神经网络结构完全一样

• 不同的是价值网络

  • RwB 的价值网络只作为 baseline，不评价策略网络，用于降低随机梯度造成的方差；
  • A2C 的价值网络时critic，评价策略网络；

• RwB 是 A2C 的特殊形式。这一点下面 14.7 后会讲。

14.7 A2C with m-step

单步 A2C 就是上面所讲的内容，具体请见 14.5.b。

而多步A2C就是使用 m 个连续 transition：

• \(y_t=\sum_{i=0}^{m-1}\gamma^i\cdot r_{t+1}+\gamma^m\cdot v(s_{t+m};w)\)
• 具体参见m-step
• 剩下的步骤没有任何改变，只是 TD target 改变了。

下面解释 RwB 和 A2C with m-step 的关系：

• A2C with m-step 的TD target：\(y_t=\sum_{i=0}^{m-1}\gamma^i\cdot r_{t+1}+\gamma^m\cdot v(s_{t+m};w)\)
• 如果使用所有的奖励，上面两项中的第二项（估计）就不存在，而第一项变成了
  • \(y_t=u_t=\sum_{i=t}^n \gamma^{i-t}\cdot r_i\)
  • 这就是 Reinforce with baseline.

x. 参考教程

• 视频课程：深度强化学习（全）_哔哩哔哩_bilibili
• 视频原地址：https://www.youtube.com/user/wsszju
• 课件地址：https://github.com/wangshusen/DeepLearning