强化学习-学习笔记3 | 策略学习
继续学习强化学习，介绍强化学习另一大分支策略学习，以及策略学习的一种经典实现方式Policy Network，以及策略网络 的训练算法 策略梯度算法。
Policy-Based Reinforcement Learning. 策略学习。
本讲用一个神经网络来近似 policy 函数，即 Policy Network，策略网络。
3. 策略学习
3.1 策略函数
我们回顾一下 策略函数 Policy Function ：
策略函数 \(\pi(a | s)\)是一个 概率密度函数（PDF），输入时当前状态s，输出为一个概率分布，表征每个 action 的概率，
拿到 策略函数 输出的 概率密度 后，agent 面向所有动作做一次随机抽样，但各个动作的概率不同。
策略学习的思路即，有了合适的 策略函数，我们就能很好的控制 agent 自动地运动 。
问题与 价值学习 的相近：我们事先并不知道这样一个策略函数，我们如何得到一个近似的策略函数呢？
如果 一个小游戏只有 5个状态10个动作，那么画一张表，通过反复地游戏得到它们的概率填入表中即可，但事实上游戏十分复杂。
我们需要做函数近似，通过学习来近似 策略函数。而函数近似的方法很多，神经网络就是其中的一种，用于近似策略函数的神经网络就是 Policy Network。
3.2 策略网络
Policy Network.
用策略网络\(\pi(a|s;\theta)\)来近似\(\pi(a|s)\)，其中 θ 是神经网络的参数，初始的 θ 是随机初始化的，通过后续的学习来改进 θ 。
比如对于超级玛丽这样的游戏：
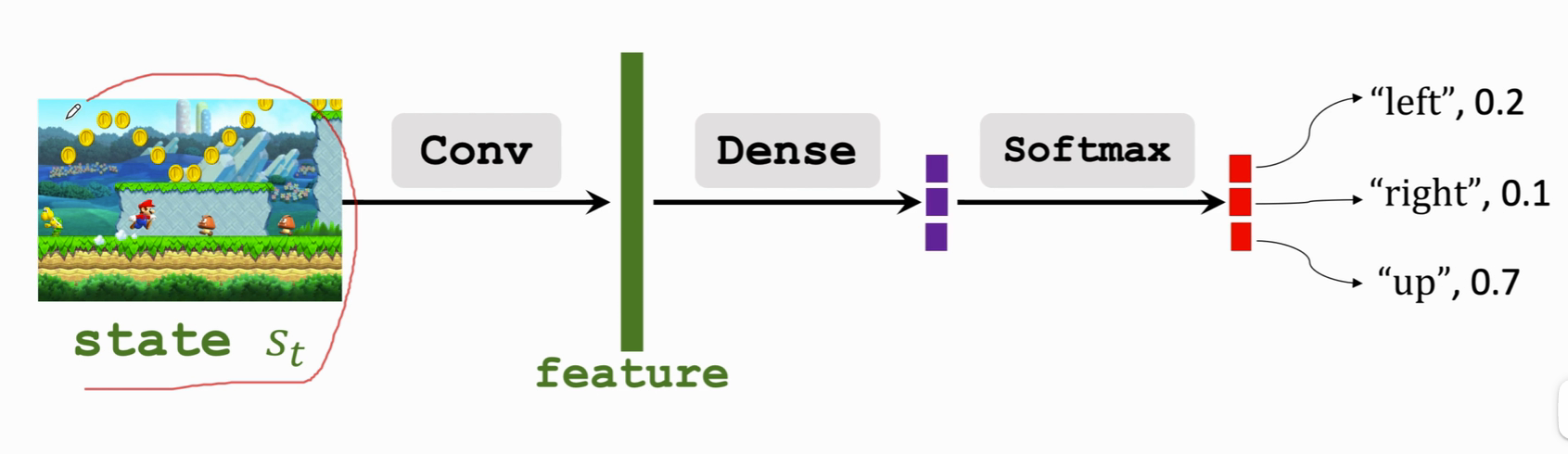
状态画面经过卷积 Conv 提取特征，特征经过全连接层 Dense 再通过 softmax 层（归一化）得到一个动作的概率分布，动作的概率集合全部加起来要等于1。
3.3 状态价值函数回顾
State-Value-Function.
折扣回报函数：
- \(U_t=R_t+\gamma R_{t+1}+\gamma^2 R_{t+2}+\gamma^3 R_{t+3}+\cdots\)
动作价值函数：
- \(Q_\pi(s_t,a_t) = \mathbb{E}[U_t|S_t=s_t,A_t=a_t]\)
- 评价在状态 \(s_t\) 的情况下做出动作 \(a_t\) 的好坏程度。
状态价值函数
- \(V_{\pi}(s_t) = \mathbb{E}_A[Q_\pi(s_t,A)]\)
- 消掉了动作 A ，这样 \(V_\pi\) 只跟状态 s 与策略函数 \(\pi\) 有关了。
- 给定 \(\pi\)，可以评价当前状态的好坏；给定状态\(s_t\)，可以评价策略 \(\pi\) 的好坏。
- 展开：
- \(V_{\pi}(s_t) = \mathbb{E}_A[Q_\pi(s_t,A)]=\sum_a\pi(a|s_t)\cdot Q_\pi(s_t,a)\)这里动作是离散的。
- \(V_{\pi}(s_t) = \mathbb{E}_A[Q_\pi(s_t,A)]=\int\pi(a|s_t)\cdot Q_\pi(s_t,a) da\)这里动作是连续的
3.4 策略学习的主要思想
基于上面的回顾，状态价值函数：
下面我们要用 神经网络 来近似 状态价值函数：
-
用策略网络 \(\pi(a|s;\theta)\) 来近似 \(\pi(a|s)\)
-
把 \(\pi(a|s_t)\) 函数替换成 \(\pi(a|s_t;\theta)\)，即为：
\(V(s_t;\theta) = \sum_a\pi(a|s_t;\theta)\cdot Q_\pi(s_t,a)\)
这样，状态价值函数就可以写成：\(V(s;\theta) ，V\) 可以评价策略网络的好坏，给定状态 S ，策略网络越好 V 的值就越大。可以通过改进参数 \(\theta\)，让$V(s;\theta) $变大。
基于上述想法，可把目标函数定义为 \(V(s;\theta)\) 的期望 ：\(J(\theta)=\mathbb{E}_{S}[V({S};\theta)]\)，期望是关于状态 S 求的，这样我们的目标就是改进\(\theta\)，使得 \(J(\theta)\) 越大越好。
J 函数可以理解为，使用策略函数 \(\pi\) ，agent的胜算有多大。
如何改进 \(\theta\) ? 即使用策略梯度算法(Policy gradient ascent)
-
观测到状态 s，这个 s 是从状态的概率分布中随机抽样出来的。
-
把$V(s;\theta) $关于 s 求导可以得到一个梯度，然后用梯度上升来更新 \(\theta\)，\(\beta\)是学习率。
\(\theta \leftarrow \theta +\beta\cdot \frac{\partial V(s;\theta)}{\partial \theta}\)
注意：我们这里算的是 V 关于 \(\theta\) 的导数，是一个随机梯度，随机性来源于状态 s
为什么要用梯度上升，因为我们想让目标函数 \(J(\theta)\) 变得越来越大。
其中 \(\frac{\partial V(s;\theta)}{\partial \theta}\) 被叫做 Policy gradient 策略梯度。
3.5 策略梯度算法
策略梯度是 V 函数 对 策略神经网络参数 \(\theta\) 的导数。
策略梯度算法的推导后续补上，目前按照视频听懂了，但是推导过程还不够严谨。
a. 两种形式
-
\(\pi\) 关于 θ 的导数 ✖ \(Q_\pi\)，再做连加；
\(\frac{\partial V(s;\theta)}{\partial \theta}=\sum_a\frac{ \partial \pi(a|s;\theta) }{\partial \theta}\cdot Q_\pi(s,a)\)
-
\(\log\pi\) 关于 \(\theta\) 的导数，乘以 \(Q_\pi\)，再关于随机变量 A 求期望。
\(\frac{\partial V(s;\theta)}{\partial \theta}=\mathbb{E}_{A\sim\pi(\cdot|s;\theta)}[\frac{ \partial log\pi(A|s;\theta) }{\partial \theta})\cdot Q_\pi(s,a)\)
这两种形式是等价的。
b. 计算梯度
有了前面两个公式，来计算策略梯度：
如果动作是离散的：可以使用第一个公式：
\(\frac{\partial V(s;\theta)}{\partial \theta}=\sum_a\frac{ \partial \pi(a|s;\theta) }{\partial \theta}\cdot Q_\pi(s,a)\)
-
对于每个动作 a , 计算 \(f(a,\theta)=\frac{\partial{\pi(a|s;\theta)}}{\partial\theta}\cdot{Q_\pi(s,a)}\)
-
策略梯度就是把 每个动作的 f 值 加起来：
$ \frac{\partial{V(s;\theta)}}{\partial \theta}=f(a_1,\theta)+f(a_2,\theta)+...+f(a_n,\theta)$
而对于连续的动作，使用第二个公式：
\(\frac{\partial V(s;\theta)}{\partial \theta}=\mathbb{E}_{A\sim\pi(\cdot|s;\theta)}[\frac{ \partial log\pi(A|s;\theta) }{\partial \theta})\cdot Q_\pi(s,a)\)
要求期望的话，需要对 A 进行定积分，而这不可能，因为 \(\pi\) 函数是一个复杂的神经网络，无法通过数学公式积分。只能通过蒙特卡洛近似来近似的算出来：
-
根据概率密度函数 \(\pi\) 随机抽样得到一个动作 \(\widehat{a}\) ,
-
计算 \(g(\widehat{a},\theta)=\frac{\partial{log\pi(\widehat{a}|s;\theta)}}{\partial\theta}\cdot Q_\pi(s,\widehat{a})\)
注意这里的 \(\widehat{a}\)是抽样出来的已确定的值。
-
根据公式2，g 函数 关于 A 求期望即为策略梯度:
\(\mathbb{E}_{A}[g(\widehat{a},\theta)] = \frac{\partial V(s;\theta)}{\partial \theta}\)
-
由于 \(\widehat{a}\) 是随机抽出来的，，所以 g 函数是 策略梯度的无偏估计。
-
由于4中结论，所以可以使用 g函数来近似 策略梯度，这就是蒙特卡洛近似。
蒙特卡洛近似：
随机抽取一个或很多个样本，用随机样本来近似期望。
mark 一个课程 CS285 Lecture。
c. 算法过程
- 在 t 时刻观测到状态 \(s_t\) ，接下来用蒙特卡洛近似来计算策略梯度
- 把策略网络 \(\pi(\cdot|{s};\theta)\) 作为概率密度函数随机采样动作 \(a_t\)。
- 计算价值函数的值，记作\(q_t \approx Q_\pi(s_t,a_t)\)
- 对策略网络 \(\pi\) 求导，得到向量矩阵或者张量：\(d_{\theta,t}=\frac{\partial log \pi(a_t|s_t,\theta)}{\partial \theta}|\theta=\theta_t\)
- 近似计算策略梯度：\(g(a_t,\theta_t) = q_t \cdot d_{\theta,t}\)
- 更新策略网络：\(\theta_{t+1}=\theta_t+\beta \cdot g(a_t,\theta_t)\)，梯度上升，为了让价值函数 V 变大。
其实上面还有一点没说，就是 \(q_t\) 怎么计算？，即 \(Q_\pi\)怎么计算。
方法1：Reinforce 算法
用策略网络 \(\pi\) 来控制 agent 运动，从一开始玩到游戏结束，把整个游戏轨迹都记录下来：
观测到所有奖励 r ,就可以算出折扣回报 \(u_t = \sum_{k=t}^{T}\gamma^{k-t}r_k\)。
由于\(Q_\pi(s_t,a_t) = \mathbb{E}[U_t]\)，所以可以使用\(u_t\)来近似$Q_\pi(s_t,a_t) $
即使用\(q_t = u_t\)
总结就是用观测到的$ u_t\(来代替\)Q_\pi(s_t,a_t)$函数
方法2：用一个神经网络来近似\(Q_\pi\)
原本已经拿神经网络来近似一个策略函数 \(\pi\)，现在又拿另一个神经网络近似 \(Q_\pi\) ，这样就有了两个神经网络，对于两个神经网络就涉及到了Actor-Critic。
3.6 总结
策略学习的思路是，我们如果能够得到一个好的 策略函数 \(\pi\) ，我们就能用 \(\pi\) 自动控制 agent 。即：\(a_t \sim\pi(\cdot | s)\)
为了得到这样一个策略函数，我们使用一个 神经网络 Policy Network \(\pi(a|s;\theta)\) 来近似策略函数。
要得到神经网络需要得到它的参数 θ，求解的算法是策略梯度算法；策略梯度就是价值函数关于θ的导数。算出θ后用梯度上升来迭代θ，以使得目标函数\(J(\theta)=\mathbb{E}_{S}[V({S};\theta)]\)越大越好。
