程序语言与编程实践4-> 蓝桥杯C/C++备赛记录2 | 第二周学习训练
0323,又是一周星期三,按道理该总结了。这周前几天写题比较多,后面事情多了起来,就没怎么写了。主要方向是洛谷的基本语法熟悉,PTA平台数据结构的一些题目。
0323附上: 题目比较多,所以文章可能有点长。
00 0317
00-1 P1116 车厢重组
00-1-1 题目描述
在一个旧式的火车站旁边有一座桥,其桥面可以绕河中心的桥墩水平旋转。
一个车站的职工发现桥的长度最多能容纳两节车厢,如果将桥旋转180度,则可以把相邻两节车厢的位置交换,
用这种方法可以重新排列车厢的顺序。于是他就负责用这座桥将进站的车厢按车厢号从小到大排列。
他退休后,火车站决定将这一工作自动化,其中一项重要的工作是编一个程序,
输入初始的车厢顺序,计算最少用多少步就能将车厢排序。
输入格式
共两行。
第一行是车厢总数N (N≤10000)。
第二行是 N 个不同的数表示初始的车厢顺序。
输出格式
一个整数,最少的旋转次数。
00-1-2 输入输出样例
输入
4
4 3 2 1
输出
6
00-1-3 解决代码
这道题,有一点意思,因为题目中没有告诉我们排序的操作过程,因此我们会去想示例的排序次数是怎么得出来的,所以我们写的程序就会是冒泡排序或者其他,再在冒泡排序中计数。
但我正要手写排序的时候,突然想起来实际上根本用不着,只输出移动次数意味着什么?意味着只需要统计一个数字前面有几个比它大,所以我们统计序列里每个数字前的count就可以啦。
题解最高赞也是我这个想法!-_-!
#include<iostream>
using namespace std;
int main(){
int N,count = 0;
cin >> N;
int train[N] = {0};
for(int i = 0; i < N; i++){
cin >> train[i];
}
//查一个数前面有几个比他大
for(int i = 0; i < N; i++){
for(int j = 0; j < i; j++){
if(train[j] > train[i]){
count++;
}
}
}
cout << count;
return 0;
}
00-2 P1146 硬币翻转
00-2-1 题目描述
在桌面上有一排硬币,共N枚,每一枚硬币均为正面朝上。
现在要把所有的硬币翻转成反面朝上,规则是每次可翻转任意N-1枚硬币
(正面向上的被翻转为反面向上,反之亦然)。
求一个最短的操作序列(将每次翻转N-1枚硬币成为一次操作)。
输入格式
一个自然数N(N为不大于100的偶数)。
输出格式
第一行包含一个整数S,表示最少需要的操作次数。接下来的S行每行分别表示每次操作后桌上硬币的状态
(一行包含N个整数(0或1),表示每个硬币的状态:
0――正面向上,和1――反面向上,不允许出现多余空格)。
对于有多种操作方案的情况,则只需操作的字典序最小输出一种。
注:操作的字典序:对于一次操作,1表示翻转,0表示不反转。
但是需要你输出的是每一次操作完的状态,0表示正面朝上,1表示反面朝上。
00-2-2 输入输出样例
输入
4
输出
4
0111
1100
0001
1111
00-2-3 解决代码
这是个很简单的题,但是需要会读题......每次反转n-1等价于每次翻一个,再把n个全翻一次。
- 如果n是偶数,执行n次以上的操作第二步就被抵消了,只执行第一步,所以输入n就可以输出n作为答案;
- 如果n是奇数,相当于执行n次第一步,然后把所有的硬币翻一次面,这样就无法实现翻面。这种情况不可能。
接着就是每一组翻动都输出01序列就好了。
#include<iostream>
using namespace std;
int main(){
int n;
int coin[105] = {0};
cin >> n;
cout << n << endl;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
if(j!=i){
coin[j] = 1 - coin[j];
}
cout << coin[j];
}
cout <<endl;
}
return 0;
}
01 0318
01-1 P1150Peter 的烟
01-1-1 题目描述
Peter 有 n 根烟,他每吸完一根烟就把烟蒂保存起来,
k(k>1)个烟蒂可以换一个新的烟,那么 Peter 最终能吸到多少根烟呢?
输入格式
每组测试数据一行包括两个整数 n, k(1 < n, k <= 10^8)。
输出格式
对于每组测试数据,输出一行包括一个整数表示最终烟的根数。
01-1-2 输入输出样例
输入 1
4 3
输出1
5
输入2
10 3
输出2
14
01-1-3 解决代码
这道题我想了一会儿,发现这件事情并不难,只需要一个循环就可以实现,只不过需要不断更新香烟的总数n,有一点剩余定理无限逼近的味道。但是题目是整数,所以总会到达。 可以举一个具体的迭代过程来看: 以4 3 为例:
i=1 <4, i%3!=0,继续;
i=2 <4,i%3!=0,继续;
i=3 <4, i%3==0, n++;
i=4 <5, i%3!=0, 继续;
i=5 =5, i%3!=0,继续;
i=6 >6,结束

#include<iostream>
using namespace std;
int main(){
int n, k;
cin >> n >> k;
int count = n ;
int sum = k;
for(int i = 1; i <= n; i++){
if(i%k==0)n++;
}
cout << n;
}
01-2 P1151 子数整数
01-2-1 题目描述

01-2-2 输入输出样例
输入(0<k<1000)
15
输出
22555
25555
28555
30000
01-2-3 解决代码
这道题不是很难,也让我意识到该复习一些算法和数据结构了。对于10000到30000的这些整数,每一个都求出它的三个子数,进行判断即可。
这道题提交了两次,原因是没有把题目看完全,题目中说若没有符合条件的,则输出"No",我没有考虑到,所以就有测试用例出错了。
#include<iostream>
using namespace std;
int main(){
int k;
cin >> k;
int sub1,sub2,sub3;
int flag = 0;//得设计一个标志位。
for(int i = 10000; i <= 30000; i++){
sub1 = i/100;
sub2 = (i-i/10000*10000)/10;
sub3 = i%1000;
if(sub3%k==0&&sub2%k==0&&sub1%k==0){
flag = 1;
cout<<i <<endl;
}
}
if(!flag)cout << "No"<<endl;
return 0;
}
01-3 P1152 欢乐的跳
01-3-1 题目描述 & 输入输出样例
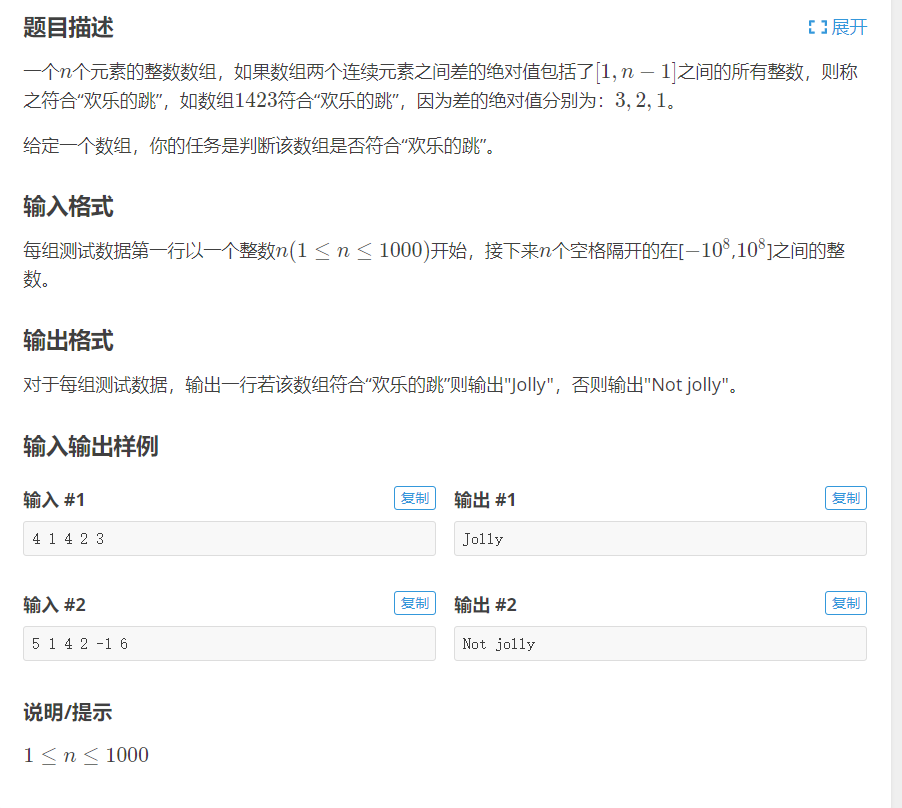
01-3-3 解决代码
这道题其实也没啥好说的,新建一个数组来记录两相邻元素的差,再取个绝对值,进行逐项判断。不过自己对于while的语法有些忘了,题目的要求也没有看清楚。
取绝对值的函数:
#include<stdlib.h>内,有abs()函数,可以对整型变量求绝对值;
#include<math.h>内,有fabs()函数,可以对浮点型变量求绝对值;
#include<iostream>
#include<math.h>
#include<stdlib.h>
using namespace std;
int main(){
int n;
cin >> n;
int jolly[n]= {0};
int jump[n-1] = {0};
for(int i = 0; i < n; i++){
cin >> jolly[i];
}//第一次是忘了输入数组》。。
int t = 0,j=1,i=0;
while(j!=n){
jump[t++]=jolly[j++]-jolly[i++];
}//3 2 -1
//第二次是把循环条件写成了j==n,属于是太久不用while了
int flag=0;
for(int i = 0; i < n-1; i++){
if(abs(jump[i])<n&&abs(jump[i])>0){
flag ++;
}
}
if(flag==n-1)cout<<"Jolly"<<endl;
else{
cout << "Not jolly"<<endl;
}
//第三次是Not Jolly报错,Jd
return 0;
}
//属实是麻了,Not jolly要小写,麻了。
01-4 01-复杂度3 二分查找
01-4-1 题目描述
函数接口定义:
Position BinarySearch( List L, ElementType X );
其中List结构定义如下:
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
L是用户传入的一个线性表,其中ElementType元素可以通过>、==、<进行比较,并且题目保证传入的数据是递增有序的。函数BinarySearch要查找X在Data中的位置,即数组下标(注意:元素从下标1开始存储)。找到则返回下标,否则返回一个特殊的失败标记NotFound。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10
#define NotFound 0
typedef int ElementType;
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
List ReadInput(); /* 裁判实现,细节不表。元素从下标1开始存储 */
Position BinarySearch( List L, ElementType X );
int main()
{
List L;
ElementType X;
Position P;
L = ReadInput();
scanf("%d", &X);
P = BinarySearch( L, X );
printf("%d\n", P);
return 0;
}
/* 你的代码将被嵌在这里 */
01-4-2 输入输出
输入样例1:
5
12 31 55 89 101
31
输出样例1:
2
输入样例2:
3
26 78 233
31
输出样例2:
0
01-4-3 解决代码
在mooc上用浙大的数据结构mooc来温习数据结构的知识,提供了一个高质量的题测平台PTA,当然要用起来,同时洛谷的入门题刷着也有点没意思了,每次只检查一些语法的问题以及思考的角度,对于高阶的结构和算法都不怎么涉及,是时候更进一步了,所以来了一道PTA的数据结构题...
虽然是二分查找但还是有一点折磨(虽然思路很简单但是做法很难一遍过)...平台的测试用例有一些刁钻,我拿当时学数据结构时已经通过的代码来提交也会报错。推荐一个二分查找讲的很好的视频.讲解的模板考虑很全面。
//01二分查找
Position BinarySearch( List L, ElementType X ){
int head = 0, tail = L->Last+1;
while(head+1!=tail){
int mid = head+(tail-head)/2;
if(L->Data[mid]==X){
return mid;
}
if(L->Data[mid]>X){
tail = mid;
}
if(L->Data[mid]<X){
head = mid;
}
}
return NotFound;
}
01-5 02-线性结构1 两个有序链表序列的合并
01-5-1 题目描述
题要求实现一个函数,将两个链表表示的递增整数序列合并为一个非递减的整数序列。
函数接口定义:
List Merge( List L1, List L2 );
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L1和L2是给定的带头结点的单链表,其结点存储的数据是递增有序的;函数Merge要将L1和L2合并为一个非递减的整数序列。应直接使用原序列中的结点,返回归并后的带头结点的链表头指针。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node {
ElementType Data;
PtrToNode Next;
};
typedef PtrToNode List;
List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表;空链表将输出NULL */
List Merge( List L1, List L2 );
int main()
{
List L1, L2, L;
L1 = Read();
L2 = Read();
L = Merge(L1, L2);
Print(L);
Print(L1);
Print(L2);
return 0;
}
/* 你的代码将被嵌在这里 */
01-5-2 输入输出
输入样例:
3
1 3 5
5
2 4 6 8 10
输出样例:
1 2 3 4 5 6 8 10
NULL
NULL
01-5-3 解决代码
写一个二分已经有点难了,写有序链表合并确实也有点困难,不过这种困难来自于手法上的生疏,想法上有力了很多(也有可能是学习了后续课程算法设计的缘故,算法讲授的更宏观)。
这个问题很简单,分别遍历AB两个链表,逐结点比较,如果符合插入条件,则执行插入操作,如果不满足,指针继续向后移动,直到两者中的一者到达链表边界(空);然后将后续未比较内容直接链过来。
List Merge(List L1,List L2){
List L3,p,q,l0;
L3 = (List)malloc(sizeof(List));
l0=L3;
p = L1->Next;
q = L2->Next;
//算法编程里这种变量更容易敲,虽然项目里不喜欢
L3->Next = NULL;
while(p&&q)
{
if(p->Data<=q->Data)
{
l0->Next = p;
l0 = l0->Next;
p=p->Next;
}
else{
l0->Next = q;
l0 = l0->Next;
q=q->Next;
}
}
l0->Next = p?p:q;
// if(p)
// {
// l0->Next=p;
// }
// if(q)
// {
// l0->Next = q;
// }
L1->Next=NULL;
L2->Next=NULL;
//合并完成两链表置空,题目要求的事情一定要做
return L3;
}
02 0319
02-1 01-复杂度1 最大子列和问题
02-1-1 题目描述
给定K个整数组成的序列{ N1, N2, ..., Nk },“连续子列”被定义为{ Ni, Ni+1, ..., Nj },其中 1≤ i ≤ j ≤ K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 },其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序,计算给定整数序列的最大子列和。
本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下:
- 数据1:与样例等价,测试基本正确性;
- 数据2:102个随机整数;
- 数据3:103个随机整数;
- 数据4:104个随机整数;
- 数据5:105个随机整数;
输入格式:
输入第1行给出正整数*K* (≤100000);第2行给出*K*个整数,其间以空格分隔。
输出格式:
在一行中输出最大子列和。如果序列中所有整数皆为负数,则输出0。
02-1-2 输入输出
输入样例:
6
-2 11 -4 13 -5 -2
输出样例:
20
01-1-3 解决代码
这道题半年前可能不太会,现在是有一定思路的。可以规定两个指针,一个指针负责从头到尾的主遍历确定头元素,第二个指针负责通过遍历改变尾元素,一首一尾就能确定一个子列。这道题还没有让输出最大子列和对应的那个子列,所以只需要设置一个max,不断更新即可。
所以很简单:
不过写的时候还是犯了低级错误,即输入输出数组的时候不是A[i],而是A[k],所以一直得不到正确结果。
//0319最大子列和
#include<iostream>
using namespace std;
int main(){
int K;
cin >> K;
int A[K]={0};
for(int i = 0; i < K; i++){
cin >> A[i];
}
//输入完成
//计算
// for(int i = 0; i < K; i++){
// cout << A[i];
// }
int sum = 0, tag = 0, count = 0;
for(int i = 0; i < K; i++){
count = A[i];
if(count>=sum)sum = A[i];
if(A[i]<0)tag++;
//cout << count<<endl;
for(int j = i+1; j < K;j++){
//cout << j << " ";
count+=A[j];
//cout << count<<endl;
if(count >= sum){
sum = count;
}
}
}
if(tag < K){
cout << sum;
}
else{
cout <<0;
}
return 0;
}
//思路没问题,数组的输入输出写错了,我麻了呀。
02-2 01-复杂度2 Maximum Subsequence Sum
02-2-1 题目描述
给定一个序列K整数 {N1,N2, ...,NK}.连续子序列定义为 {Ni,Ni+1, ...,Nj} 其中1≤ i ≤ j ≤ K.最大子序列是具有其元素最大和的连续子序列。例如,给定序列 { -2, 11, -4, 13, -5, -2 },其最大子序列为 { 11, -4, 13 },最大和为 20。
现在,您应该找到最大总和,以及最大子序列的第一个和最后一个数字。
输入规格:
每个输入文件包含一个测试用例。每个案例占用两行。第一行包含正整数K (≤10000).第二行包含K数字,以空格分隔。
输出规格:
对于每个测试用例,在一行中输出最大和,以及最大子序列的第一个和最后一个数字。数字必须用一个空格分隔,但行尾不得有多余的空格。如果最大子序列不是唯一的,请输出索引最小的子序列我和j(如示例案例所示)。如果所有K数字为负数,然后其最大和定义为 0,并且您应该输出整个序列的第一个和最后一个数字。
02-2-2 输入输出
示例输入:
10
-10 1 2 3 4 -5 -23 3 7 -21
示例输出:
10 1 4
02-2-3 解决代码
这道题是上一道题的加强版,要求在输出最大子列和的同时输出这个子列的头尾元素。
就我上道题的思路,实现这一个升级是很简单的,增加两个标记位即可,遇到最大值就把头尾存下来。同时它强调输出下标较小的,所以要把上道题中的 ">=" 改成 ">" 。
第一次提交,感觉已经很周全了,出现了部分正确:
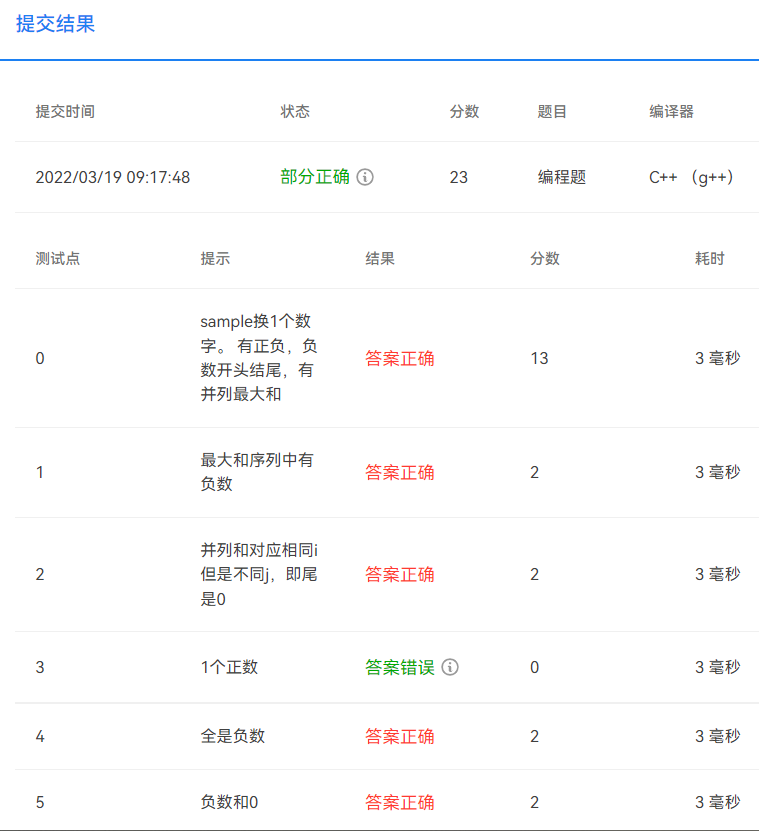
一个正数的情况出错。稍加检查发现我用来甄别在一个数出取得最大子列和的地方出错,写成了:
for(int i = 0; i < K; i++){
count = A[i];
if(count>sum){
sum = A[i];
left = i;
right = i;
//应当是left = A[i],left和right都应该是。
}
代码如下:
//0319加强版的最大子列
//需要在输出最大子列和的同时输出首尾元素,用我的思路来讲,只需要增加两个标记位罢了。
#include<iostream>
using namespace std;
int main(){
int K;
cin >> K;
int A[K]={0};
for(int i = 0; i < K; i++){
cin >> A[i];
}
//输入完成
//计算
// for(int i = 0; i < K; i++){
// cout << A[i];
// }
int sum = 0, tag = 0, count = 0;
int left = 0, right = 0;//增加两个标记位
for(int i = 0; i < K; i++){
count = A[i];
if(count>sum){
sum = A[i];
left = A[i];
right = A[i];
}
if(A[i]<0)tag++;
//cout << count<<endl;
for(int j = i+1; j < K;j++){
//cout << j << " ";
count+=A[j];
//cout << count<<endl;
if(count > sum){
sum = count;
left = A[i];
right = A[j];
//cout << sum<<" "<< left << " "<<right<<endl;
}
}
}
if(tag < K){
cout << sum<<" "<< left << " "<<right<<endl;
}
else{
cout << 0 <<" " << A[0] << " " << A[K-1];
}
return 0;
}
03 0320 / 0322
0320开了这个题,但是没写,去写计组的一个实验测试题了,有些难度,写了半天,所以就没有刷题。
0321打开又想了一会,觉得加法有点思路,乘法实现起来还是有点陌生,去写计组作业和微机接口mooc去了。
0322晚上终于得空,把实现了一下,参照了一下别的博主的思路。
03-1 线性结构2 一元多项式的乘法与加法运算
03-1-1 题目描述
设计函数分别求两个一元多项式的乘积与和。
输入格式:
输入分2行,每行分别先给出多项式非零项的个数,再以指数递降方式输入一个多项式非零项系数和指数(绝对值均为不超过1000的整数)。 数字间以空格分隔。
输出格式:
输出分2行,分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。 数字间以空格分隔,但结尾不能有多余空格。 零多项式应输出。0 0
03-1-2 输入输出
设计函数分别求两个一元多项式的乘积与和。
输入格式:
输入分2行,每行分别先给出多项式非零项的个数,再以指数递降方式输入一个多项式非零项系数和指数(绝对值均为不超过1000的整数)。 数字间以空格分隔。
输出格式:(!这里最重要!)
输出分2行,分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。 数字间以空格分隔,但结尾不能有多余空格。 零多项式应输出。0 0
03-1-3 解决思路以及细节问题
感觉用数组可以硬做,但是用链表其实更好,本来在回忆链表的一些操作,突然想起来自己明明报了浙大的mooc,打开一看,以上的题目居然都有实现过程,不禁感叹这个mooc质量之高。
敲出来当然觉得很高兴,因为去年同期,这是很难的事情,但高兴早了,提交上去之后报错,全错,格式错误,仔细检查发现是自己的输出函数不对(下面代码输出函数的注释部分)。
又审了一遍题,发现没有认真理解题目关于输出格式的要求,要求 和多项式 和 积多项式 输出之间有一个换行,并且每一行最后不能有空字符,每一个结点的两个数之间有空格,结点和结点之间也有空格,我的代码是实现不了这些的,我只好应用了putchar().
改进之后其实还是错的(20分拿了16分),是细节之错,我觉得很有记录的必要。见这段代码下方,先来看看近乎正确代码:
//0319两个一元多次多项式的相加
//感觉有数组可以硬做,但是用链表其实更好
#include<iostream>
using namespace std;
typedef struct LNode{
int coef,exp;
LNode *next;
}LNode;
LNode *creatList(){//创建链表
int n ;
cin >> n;
LNode *head = new LNode;
head->next = NULL;
LNode *p = head;
while(n--){
LNode *q = new LNode;
q->next = NULL;
cin >> q->coef >> q->exp;
p = p->next = q;
//相当于p->next = q; p = p->next;
}
return head;
}
LNode *polyAdd(LNode* L1, LNode* L2){
L1 = L1->next;
L2 = L2->next;
//创建 和链表
LNode* head = new LNode;
head->next = NULL;
//尾插法
LNode* p = head;
while(L1 && L2){
LNode *q = new LNode;
q -> next = NULL;
if(L1->exp > L2->exp){
q->exp = L1->exp;
q->coef = L1->coef;
p = p->next = q;
L1 = L1->next;
}
else if(L1->exp < L2->exp){
q->exp = L2->exp;
q->coef = L2->coef;
p= p->next = q;
L2 = L2->next;
}
else{
q->exp = L1->exp;
q->coef = L1->coef+L2->coef;
//到这里很特别,因为等零我们是不能放进求和链表的,所以判断后删去节点q
if(q->coef == 0){
delete q;
}
else{
p= p ->next = q;
}
L1 = L1->next;
L2 = L2 ->next;
}
}
LNode* L = L1?L1:L2;
while(L){
p = p->next = L;
L = L -> next;
}
return head;//别忘了返回
}
LNode *polyMult(LNode* L1,LNode* L2){
L1 = L1->next;
L2 = L2->next;
LNode *head = new LNode;
head->next = NULL;
//说是求积,其实也不复杂,定住一条链,遍历另一条
while(L1){
LNode* headofL2 = L2;
//先保存一下L2头结点
while(L2){
LNode* p = new LNode;
p->next = NULL;
p->coef = L1->coef*L2->coef;
p->exp = L1->exp+L2->exp;
//放入求积链表需要一个操作,即找到这个结点该放入的位置
LNode* pr = head;
//移动pr,当pr的下一节点次数比当前结果小,那就把当前节点插入pr之后
while(pr->next && pr->next->exp > p->exp){
pr = pr->next;
}
//循环结束有几种情况,一种pr->next = NULL或者满足比当前结果小,就插入
//另一种相等,则相加
if(pr->next == NULL || pr ->next ->exp < p->exp){
p -> next = pr->next;
pr ->next = p;
}//插入
else{
pr->next->coef += p->coef;
//只要两结点相加,就要考虑为零的情况
if(pr->next->coef==0){
LNode* tmp = pr->next;
pr->next = tmp->next;
delete(tmp);
}
delete p;
}
L2 = L2->next;
}
//一次内循环后把L2归位
L2 = headofL2;
L1 = L1->next;
}
return head;
}
//下面需要输出函数
void printList(LNode* L){
//由于空链表需要输出 0 0,所以空时需要特别处理一下
if(L->next == NULL){//刚手敲掉了一个=
LNode *p = new LNode;
p->next = NULL;
p->coef = 0;
p->exp = 0;
}
L = L->next;
// while(L){
// //这里面还需要注意,需要调用两次这个,所以记得最后输出换行
// //cout << L->coef << " " << L-> exp<<" ";
// //L = L->next;
// //
// }
// cout<<endl;
//按照上面的写法跟题目输出的格式并不同
while(L){
cout << L->coef <<" "<< L->exp;
if(L->next)putchar(' ');
else putchar('\n');
L= L ->next;
}
}
int main(){
LNode *L1 = creatList();
LNode *L2 = creatList();
//初始化两个链表,包括输入
printList(polyMult(L1,L2));
printList(polyAdd(L1,L2));
//可以直接输出两个运算的结果
return 0;
}
但是,这一版代码提交还是有问题的,截图如下:
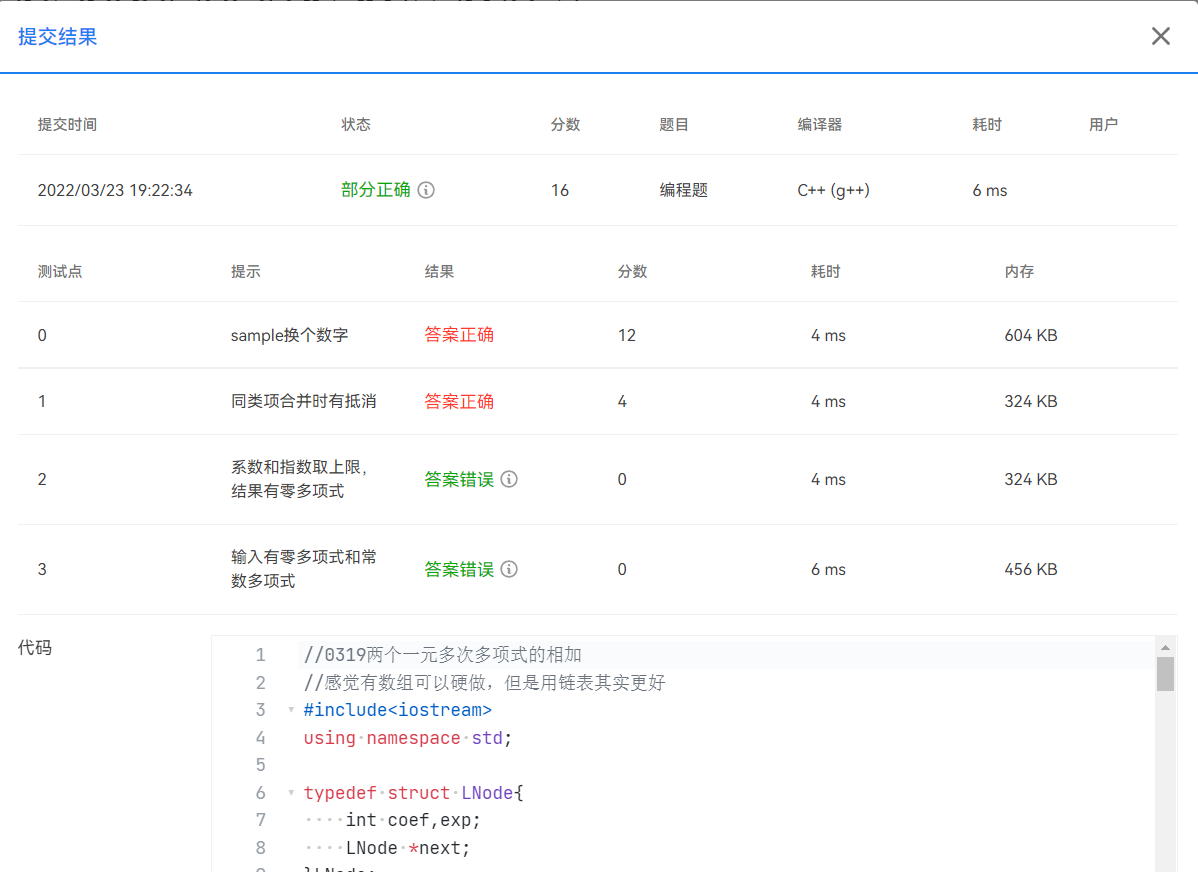
出错原因也很简单:在进行异常处理即输出0 0 的时候,自己准备用来输出0 0 的结点没有挂上去,来看看输出函数printlist是怎么漏掉的
void printList(LNode* L){
//由于空链表需要输出 0 0,所以空时需要特别处理一下
if(L->next == NULL){//刚手敲掉了一个=
LNode *p = new LNode;
p->next = NULL;
p->coef = 0;
p->exp = 0;
}
...
}
可以看到我的想法很好,如果是空链表,我新建一个结点,里面放两个0,然后把这个结点挂上去,再进行下面输出操作,就执行了,但是问题在于,if语句的最后我没有把L->nex = p;,所以产生了上面的错误。
void printList(LNode* L){
//由于空链表需要输出 0 0,所以空时需要特别处理一下
if(L->next == NULL){//刚手敲掉了一个=
LNode *p = new LNode;
p->next = NULL;
p->coef = 0;
p->exp = 0;
L->next = p;
}
...
}
03-1-4 最终代码
所以完整代码是:
//0319两个一元多次多项式的相加
//感觉有数组可以硬做,但是用链表其实更好
#include<iostream>
using namespace std;
typedef struct LNode{
int coef,exp;
LNode *next;
}LNode;
LNode *creatList(){//创建链表
int n ;
cin >> n;
LNode *head = new LNode;
head->next = NULL;
LNode *p = head;
while(n--){
LNode *q = new LNode;
q->next = NULL;
cin >> q->coef >> q->exp;
p = p->next = q;
//相当于p->next = q; p = p->next;
}
return head;
}
LNode *polyAdd(LNode* L1, LNode* L2){
L1 = L1->next;
L2 = L2->next;
//创建 和链表
LNode* head = new LNode;
head->next = NULL;
//尾插法
LNode* p = head;
while(L1 && L2){
LNode *q = new LNode;
q -> next = NULL;
if(L1->exp > L2->exp){
q->exp = L1->exp;
q->coef = L1->coef;
p = p->next = q;
L1 = L1->next;
}
else if(L1->exp < L2->exp){
q->exp = L2->exp;
q->coef = L2->coef;
p= p->next = q;
L2 = L2->next;
}
else{
q->exp = L1->exp;
q->coef = L1->coef+L2->coef;
//到这里很特别,因为等零我们是不能放进求和链表的,所以判断后删去节点q
if(q->coef == 0){
delete q;
}
else{
p= p ->next = q;
}
L1 = L1->next;
L2 = L2 ->next;
}
}
LNode* L = L1?L1:L2;
while(L){
p = p->next = L;
L = L -> next;
}
return head;//别忘了返回
}
LNode *polyMult(LNode* L1,LNode* L2){
L1 = L1->next;
L2 = L2->next;
LNode *head = new LNode;
head->next = NULL;
//说是求积,其实也不复杂,定住一条链,遍历另一条
while(L1){
LNode* headofL2 = L2;
//先保存一下L2头结点
while(L2){
LNode* p = new LNode;
p->next = NULL;
p->coef = L1->coef*L2->coef;
p->exp = L1->exp+L2->exp;
//放入求积链表需要一个操作,即找到这个结点该放入的位置
LNode* pr = head;
//移动pr,当pr的下一节点次数比当前结果小,那就把当前节点插入pr之后
while(pr->next && pr->next->exp > p->exp){
pr = pr->next;
}
//循环结束有几种情况,一种pr->next = NULL或者满足比当前结果小,就插入
//另一种相等,则相加
if(pr->next == NULL || pr ->next ->exp < p->exp){
p -> next = pr->next;
pr ->next = p;
}//插入
else{
pr->next->coef += p->coef;
//只要两结点相加,就要考虑为零的情况
if(pr->next->coef==0){
LNode* tmp = pr->next;
pr->next = tmp->next;
delete tmp;
}
delete p;
}
L2 = L2->next;
}
//一次内循环后把L2归位
L2 = headofL2;
L1 = L1->next;
}
return head;
}
//下面需要输出函数
void printList(LNode* L){
//由于空链表需要输出 0 0,所以空时需要特别处理一下
if(L->next == NULL){//刚手敲掉了一个=
LNode *p = new LNode;
p->next = NULL;
p->coef = 0;
p->exp = 0;
L->next = p;
}
L = L->next;
// while(L){
// //这里面还需要注意,需要调用两次这个,所以记得最后输出换行
// //cout << L->coef << " " << L-> exp<<" ";
// //L = L->next;
// //
// }
// cout<<endl;
//按照上面的写法跟题目输出的格式并不同
while(L){
cout << L->coef <<" "<< L->exp;
if(L->next)putchar(' ');
else putchar('\n');
L= L ->next;
}
}
int main(){
LNode *L1 = creatList();
LNode *L2 = creatList();
//初始化两个链表,包括输入
printList(polyMult(L1,L2));
printList(polyAdd(L1,L2));
//可以直接输出两个运算的结果
return 0;
}


 个人的备赛第二周的总结文档,复习了一些基本语法和数据结构,也给大家介绍几道编程基础题和几个容易出错的地方。
个人的备赛第二周的总结文档,复习了一些基本语法和数据结构,也给大家介绍几道编程基础题和几个容易出错的地方。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号