人工智能与智能系统2-> 机器人学2 | 时间与运动
《Robotics, Vision and Control》学习到第三章,我才发现这本书是有配套视频的,第二章看的好辛苦,很多地方生硬理解了一下,现在打算把视频再好好看一看,作为补充,也会记录笔记。
本系列参考资料:
-
《Robotics, Vision and Control》
-
B站公开课:
- 台湾交通大学机器人学公开课
- Peter Corke 配套视频
-
老黄的《机器人技术基础》课程讲解及PPT
-
N多有关机器人学的大佬的博客
推荐一个博客:MATLAB RTB常用公式汇整(三),我参考其修正了一些我的笔记。
00 概述
前一部分我们学习了二维三维空间中的物体位姿描述,这一部分我们主要研究物体位姿随时间变化的描述情况,为后面机器人底盘、导航、定位做铺垫。
01 轨迹
路径:从初始位姿->最终位姿的一个图形。
轨迹:路径+特定时间属性;轨迹的重要特征是平滑,位置和姿态需要随时间流畅地变化。
01-1 平滑一维轨迹
一维代表着一条直线,我们可以用一个常见的实函数就能表示出位姿随时间的变化规律。我们以五次多项式函数为例:
其轨迹方程、导数及二阶导如下:
给出这样的方程,我们就确定了位置、速度、加速度的边界。我们把t=0和t=T带入上面三个式子,可以得到一个矩阵。
s = tpoly(0, 1, 50);
%生成一个五次多项式轨迹,0~1,分50步
%输出:
s = 50×1
0.0021
0.0048
0.0091
0.0152
0.0233
0.0336
0.0461
0.0611
0.0785
0.0982
...
plot(s)
% 绘制轨迹曲线,如下:
[s, sd, sdd] = tpoly(0,1,50);
% 输出速度和加速度的情况
% 如果想对速度加速度输出
subplot(3,2,1);plot(s1);grid on;xlabel('时间');ylabel('s');
subplot(3,2,3);plot(sd1);grid on;xlabel('时间');ylabel('sd');
subplot(3,2,5);plot(sdd1);grid on;xlabel('时间');ylabel('sdd');
% 设置0~1,50步,初速度0.5,末速度为0
s1 = tpoly(0,1,50,0.5,0);
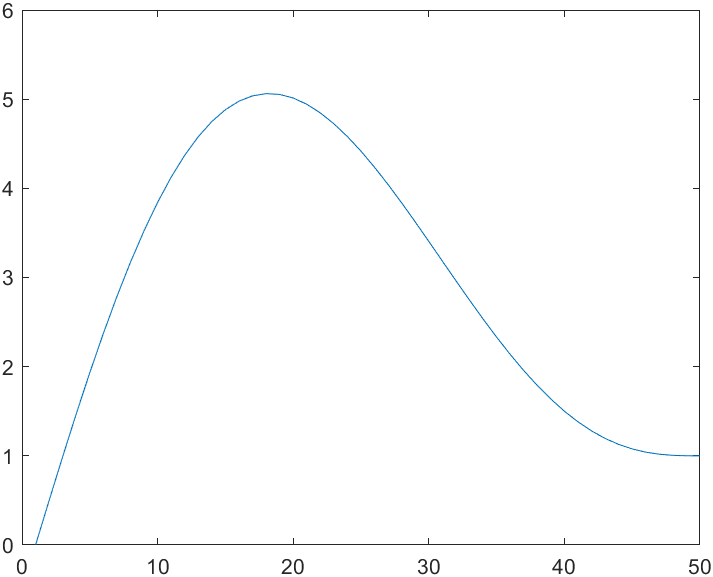
plot(s1)
% 如果想输出速度加速度,同上

-
从轨迹上看,这种情况会使得运动存在一种往复的现象,即存在一些点超过终点(一维),比如图像中的峰值为5,超出了我们0~1的范围。
-
从速度上看,第一种情况(以0为初速度),会在25s取得速度最大值(我们可以用plot绘制出来),我们可以用下面这段代码计算平均速度:
mean(sd)/max(sd) % 输出: ans = 0.5231 % 即平均速度为最大速度的52.31%
而我们知道,真正的机器人关节是有额定速度的,我们一般会希望机器人(关节)尽快到达指定的位置,即使其在速度较大的时间占比尽可能大。
一种解决方法是采用混合曲线轨迹:
s2 = lspb(0, 1, 50)
% 轨迹由一条线段(代表匀速运动)与两条抛物线组成
plot(s2)
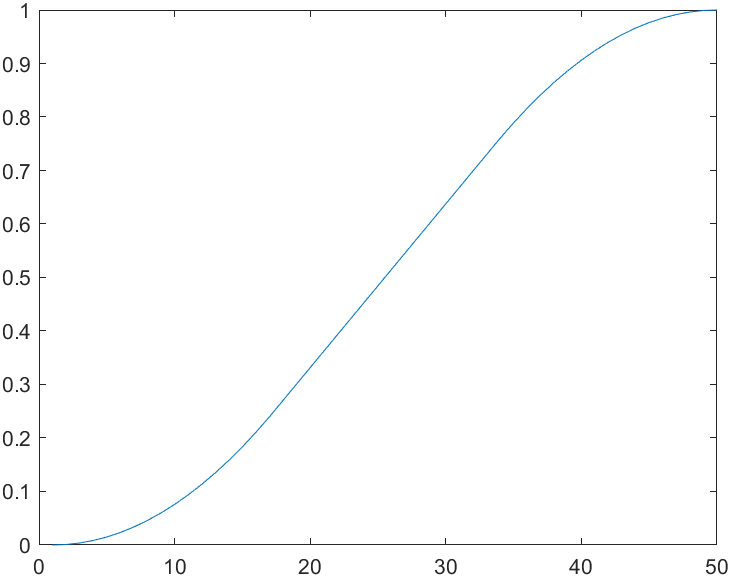
可以预见,这种运动的速度曲线是一种梯形,所以也成为梯形轨迹,普遍应用于工业马达驱动领域。
梯形轨迹的速度虽然光滑,但是加速度不光滑。
上面的lspb是默认速度,我们可以自己设置参数,给直线段一个速度(当然,速度值不是任意选择的):
% 我们先返回当前图的直线段速度作为参考
max(sd)
% 输出:
ans = 0.0306
% 再设定新参数0.025,不可行的参数会返回错误
s2 = lspb(0, 1, 50, 0.025);
01-2 多维轨迹
从前一节可以知道,我们描述一个物体大多是需要一个多维坐标向量;我们描述物体的运动,也需要对从初始位姿向量到末态初始位姿向量的多维平滑运动的描述。
在RTB中将01-1的标量轨迹扩展成多维向量还是很简单的,即使用 mtraj 函数。
x = mtraj(@tpoly, [0 2], [1 -1], 50);
% %分50个时间步从(0,2)运动到(1,-1),根据50×2的矩阵,生成一个二变量的标量轨迹
% x = mtraj(@lspb, [0 2], [1 -1], 50);
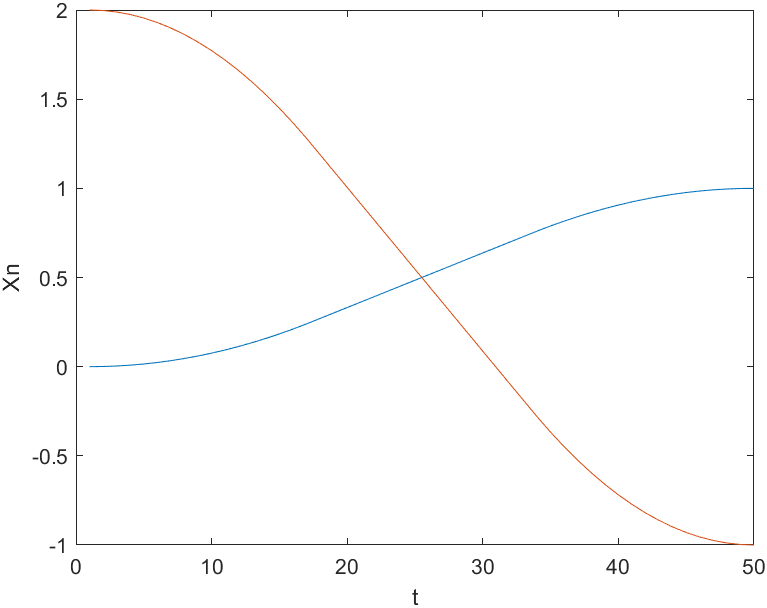
plot(x);
% 其实不标也可,横轴是时间,纵轴是各个维度x的标量
xlabel('t')
ylabel('Xn')
% 对于三维位姿,如果是三变量,如下,意义类推
x = mtraj(@tpoly, [0 2 1], [1 -1 0], 50);

如果采用lspb函数则为下图:
对于三维空间中的位姿问题,可以先用如下方法将位姿齐次矩阵T转换为一个六维向量:
x = [transl(T); tr2rpy(T)'];
% transl实现平移操作 tr2rpy是位姿齐次矩阵T->卡尔丹角(描述旋转角度)
然后再产生相应的轨迹。但是对于描述姿态的三角度插值存在一定的限制。 这点后面再提。
01-3 多段轨迹
机器人应用中经常需要平滑地沿一条路径运动,并不停顿地经过一个或多个中间点。
我们可以对问题进行具体化,即我们需要让轨迹通过可以确定这条路径的N个点Xn(位姿向量),即划分为N-1个运动区间。
下面这几段原文翻译并不好,网上博主大多也只是做了记录,但是其实不耽误有工科基础的同学看懂其中意思,我理解、整理如下:
一维
先放上原文图(有了电子书嘻嘻):

顺着上面说的意思,举个例子(如上面电子书的图3.4),我们考虑一个一维案例,毕竟从01-2我们可以看出多维只是一维的组合而已,对每个维度就是一个一维运动。
这个案例需要我们从X1到达X4,我们选取的路径决定点(中间点)为X1、X2、X3、X4,注意这里的选取并不代表我们一定要完全通过这些点,我们需要综合所有的需求规划出合理的方案。附上一维图片:

最简来讲,我们会依次连接X1-X2-X3-X4,但明显我们的速度将会变得不连续:因为X2甚至在X4的右侧,我们如果勾勒书图3.4的折线内容,会出现速度的突变。
为了实现速度连续,我们需要舍弃掉一些预定的中间点位置(实际上从计算方法\数值分析的角度很好理解),采用直线和曲线拟合的方式,如书上曲线直线组合的方式。这样书上的那个图就会很好理解:
- 从X1按要求的加速度(不一定恒定)加速至匀速速度;
- 注意这个匀速速度是可以根据需要设定的;
- 匀速运动到适宜时刻,即按照预定直线还需tacc/2时间的时刻,即图中首段直线结束时刻;
- 开始减速再反向加速的过程,图中tacc时间对应过程;
- 重复上述类似过程。
我们也可以算出第四步的平均加速度
如果这个维度对应的轴最大加速度已知,就可以计算出最小的tacc。
多维
下面我们进一步学习一下多维的情况:
如上文所说,多维只不过是将一维组合在一起。而将一维组合在一起需要考虑的最重要的问题就是,我们需要让不同维度上的点同时到达下一目标点Xk。
解决方法就是考虑简单的短板效应:我们考虑从Xk到Xk+1需要时间最久的那个维度的运动。根据额定速度和该维度距离计算出具体时间,再进一步确定各维度实际所需的速度。
Matlab实现
% mstraj()可以根据中间点矩阵生成一个多段多轴轨迹
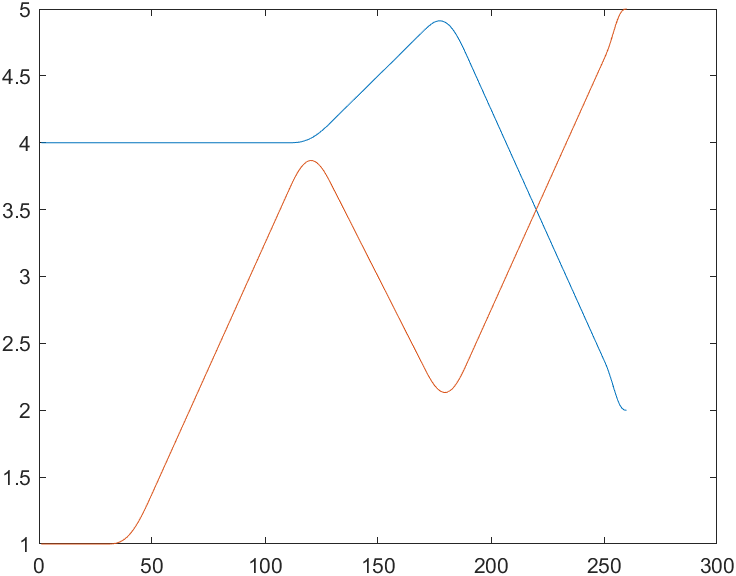
via = [4,1; 4,4; 5,2; 2,5];
q = mstraj(via, [2, 1], [], [4, 1], 0.05, 0);
% 参数:via中间点,最大速度向量,每段的时间向量,起点,采样时间间隔,加速时间,会输出一个以取样点分行的位置矩阵
plot(q)
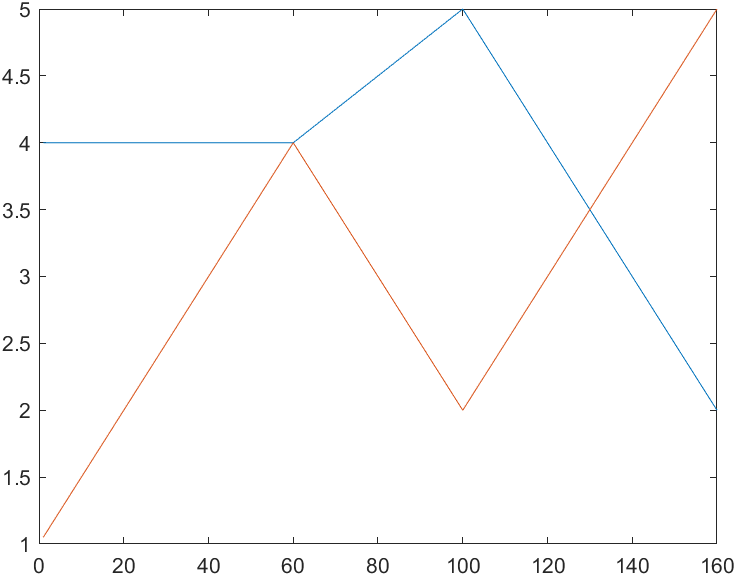
可以看到,上面的代码我们没有设定加速时间,如果设定加速时间 tacc 会使上面的折线变得圆润一些。
% mstraj()可以根据中间点矩阵生成一个多段多轴轨迹,要与生成五次多项式的mtraj区分开
q = mstraj(via, [2, 1], [], [4, 1], 0.05, );
值得注意的是,这个mstraj()参数很丰富,比如可以传入起点和终点的速度,tacc可以是一个向量,设定每一次速度改变的时间。mstraj是对向量代表的位姿进行插值,我们的例子是笛卡尔坐标系中的向量,也可以适用于三向量表示法的向量。
但是对于姿态旋转,将会有更优的插值方式:
01-4 三维空间姿态插值
typora中使用上下标:
- 上标: 内容
- 下标:内容
在机器人学中,我们经常需要对姿态进行插值。比如,我们对于末端执行器从位姿ξ0改变到ξ1,我们就需要某个连续的函数ξ(s) = σ(ξ0, ξ1, s) (s∈[0, 1]);这个函数的边界条件易知为σ(ξ0, ξ1, 0) = ξ0,σ(ξ0, ξ1, 1) = ξ1。
这里必须强调这个函数必须是光滑地经过一系列中间位姿的,如何实现取决于ξ的表示方法(上一部分讲的)。
复习插值:
在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散型数据点。
如果ξ的表示方式为正交旋转矩阵,如果使用简单的线性插值,插值得到的矩阵不正交。
复习矩阵正交:
正交矩阵满足--列向量2范数为1,&& 列向量之间正交。
三角度表示法可以实现线性插值:
但根据上一部分的内容可以知道,三角度表示法存在奇点。
单位四元数的插值法与三角度类似,见matlab表示法。
四元插值法是通过使用球形线性插值(slerp)来实现的,其中单位四元数在一个四维超球面上沿一个大圆路径运动,在三维空间就表现为绕固定轴的转动。
matlab实现
%%三角度表示法
% 定义两个姿态,分别为初态和末态
R0=rotz(-30/pi*180)*roty(30/pi*180);
R1=rotz(30/pi*180)*roty(30/pi*180);
%
% 得到等价横滚-俯仰-偏航角
rpy0 = tr2rpy(R0);
rpy1 = tr2rpy(R1);
% 分50个时间步在它们之间生成一条轨迹
rpy = mtraj(@tpoly,rpy0,rpy1,50);
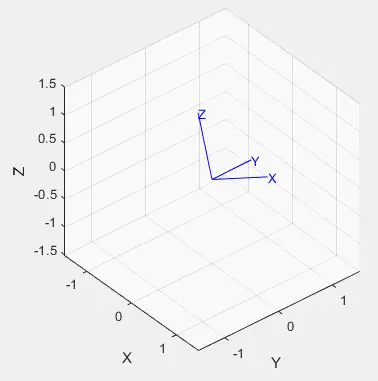
tranimate(rpy2tr(rpy));
view([-48.02 30.83]);% 调整视角使看的更清楚
% 动图目前不会保存,下面是效果图:

%%单位四元数表示:
% 我们使用上面三角度的位姿,先转换为四元数
q0 = UnitQuaternion(R0);
q1 = UnitQuaternion(R1);
% 对它们进行插值
q = interp(q0, q1,[0:49]'/49);
% 查看一下插值情况
about(q)
% 动画:
tranimate(q.T)
% 效果图如下:
01-5 笛卡尔运动
这一部分我们来研究研究齐次变换矩阵的插值。
这一问题来自于我们有时会有一个需求是:要在SE(3)中生成两位姿之间的光滑路径,这个过程会同时涉及位置、姿态的变化。机器人学中这通常被称为笛卡尔运动。
我们结合matlab实操来理解:
% 创建始末位姿:
T0 = transl(0.4, 0.2, 0)*trotx(180);
T1 = transl(-0.4, -0.2, 0.3)*troty(90)*trotz(-90);
% 这里这些角度的问题:
% trotx这些函数没有'deg'说明都应该是弧度制,这里只是为了让旋转程度更大
工具箱函数trinterp提供了沿路径单位化距离s∈[0, 1]中的位姿插值。比如:中间位姿:
trinterp(T0, T1, 0.5)
% 输出为:
ans = 4×4
0 1.0000 0 0
0 0 -1.0000 0
-1.0000 0 0 0.1500
0 0 0 1.0000
其中平移部分我们采用的是线性插值,旋转部分采用四元数插值法interp进行球形插值。
上述两个位姿之间五十个分步的轨迹可以用如下方法进行插值:
Ts = trinterp(T0, T1, [0:49]/49);
%生成每个时间步的齐次变换矩阵
% 参数分别对应起点/终点的位姿,0到1线性变化的路径长度。
about(Ts)
% 输出:
Ts [double] : 4x4x50 (6.4 kB)
% 这是每个时间分步对应的齐次变换矩阵(50个4×4矩阵)
% 我们可以查看第一个点的齐次变换
Ts(:, :, 1)
% 输出:
ans = 4×4
1.0000 0 0 0.4000
0 -1.0000 0 0.2000
0 0 -1.0000 0
0 0 0 1.0000
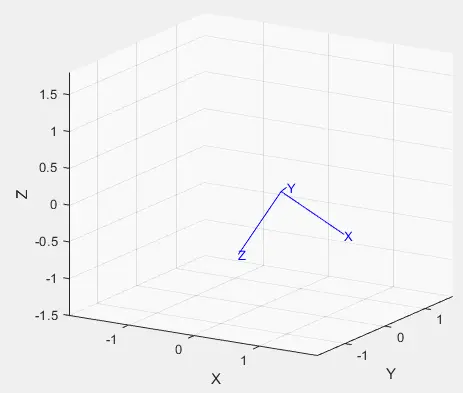
% 可以通过动画来直观展示:
tranimate(Ts)
% 它将展现出坐标系从位姿T1平移、旋转到位姿T2的变化过程。
% 该轨迹的平移部分由以下方式获得:
P = transl(Ts)
% 输出轨迹的笛卡尔位置坐标,可以对照一下我们的始末位姿。每一行对应每一时间分步上的位置向量。
P = 50×3
0.4000 0.2000 0
0.3837 0.1918 0.0061
0.3673 0.1837 0.0122
0.3510 0.1755 0.0184
0.3347 0.1673 0.0245
0.3184 0.1592 0.0306
0.3020 0.1510 0.0367
0.2857 0.1429 0.0429
0.2694 0.1347 0.0490
0.2531 0.1265 0.0551
...
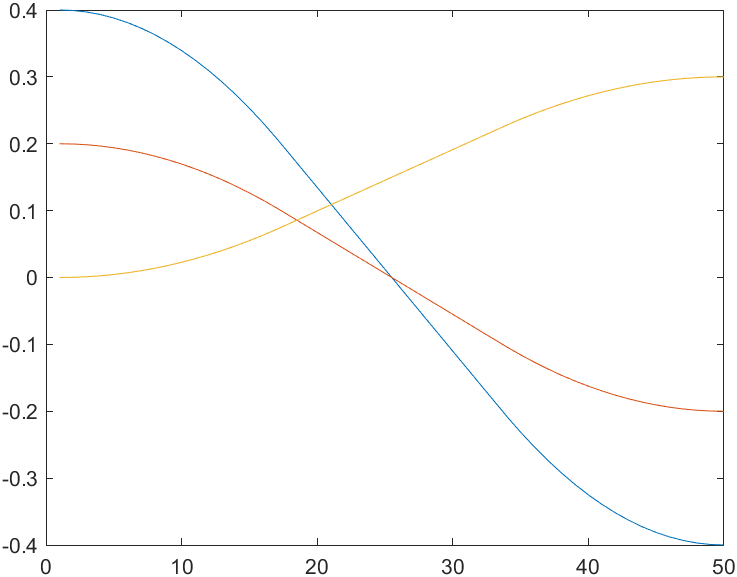
% 我们可以绘制出位置的变化:注意是位置的变化
plot(P)
另外我们还可以来看看横滚-俯仰-偏摆格式化的姿态变化曲线。
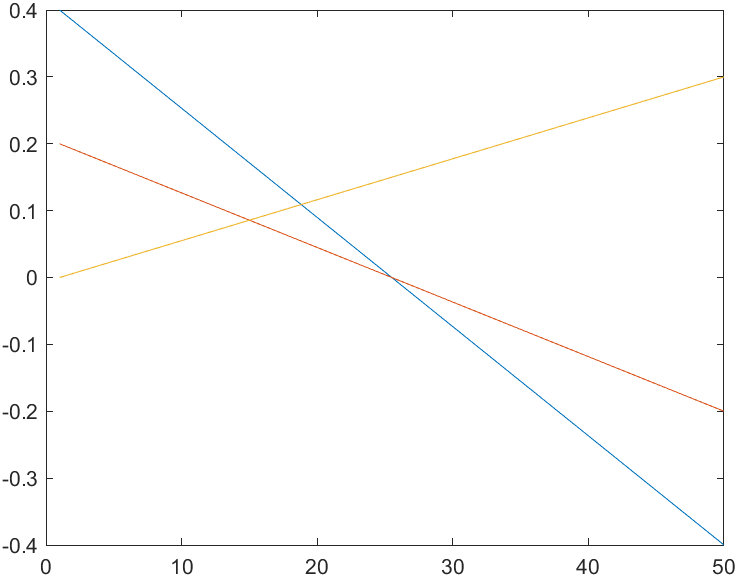
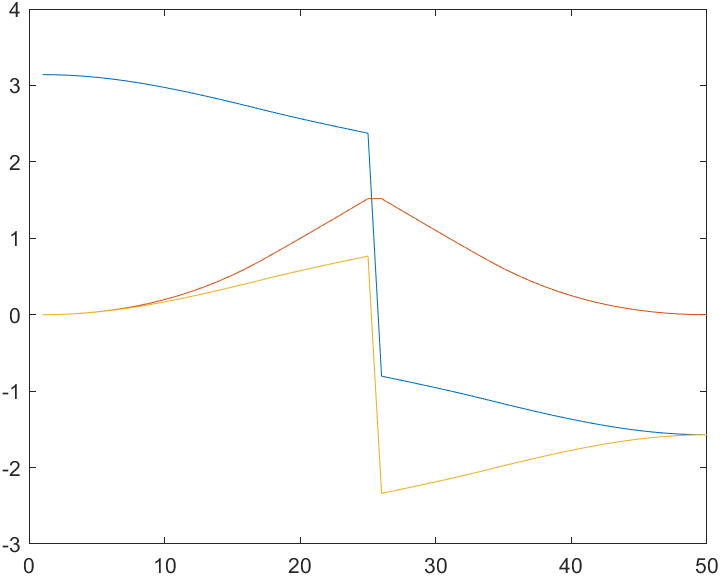
rpy = tr2rpy(Ts);
plot(rpy);

蓝:x翻滚;红色:y俯仰;黄色:z偏摆
可以看到,位置变化光滑且为线性,而姿态变化不光滑也不是线性的。非线性是因为角度表示法对于线性表示的四元数进行了非线性变换。不光滑是因为遇到了奇点。
plot还是直接连线得到的,我们可以用tpoly和lspb或者ctraj来把上面的折线平顺处理。这样做不会改变轨迹,但很明显速度和加速度会变得合理很多。
Ts1 = trinterp(T0, T1, lspb(0,1,50));
P1 = transl(Ts1)
%%
% 或是:Ts = ctraj(T0,T1,50);始末位姿+分步数量
plot(P1)
rpy1 = tr2rpy(Ts1)
plot(rpy1)
02 时变坐标系
上面我们研究了物体随时间变化的旋转和平移的轨迹问题,下面我们研究轨迹的速度。平移速度很好说,我们具体讨论旋转速度。
02-1 旋转坐标系
概念
我们考虑一个物体的旋转的时候,我们一般会用角速度向量ω=(ωx, ωy, ωz)来衡量,从大物上或许知道角速度是一个轴,是一个瞬时转动轴,向量长度表示绕该轴的旋转率。
联想到了上一部分学习的绕定轴旋转。
力学里有一个时变旋转矩阵微分表达式:
R(t)是标准正交旋转矩阵,左侧是角速度
S(ω)是一个斜对称矩阵,三维情况下具体形式如下:
matlab实现
% 要得到S(ω)矩阵
S = skew([1 2 3])
% 输出:
S = 3×3
0 -3 2
3 0 -1
-2 1 0
% vex可以逆解S,得到角速度向量
vex(S)
% 输出:
ans = 3×1
1
2
3
进一步
我们可以试着理解一下左侧:
这表示了正交旋转矩阵是如何作为一个角速度的函数变化的。
02-2 增量运动
概念推导
顺着上面的推导继续思考,我们考虑一个微小的旋转R0->R1,得到:
δθ=δtω是一个三维向量,单位是角度,表示一个绕世界坐标系xyz三轴的无穷小转动。
下面说明无穷小的角度变化的乘法是可交换的:
delta1 = rotx(0.001*180/pi)*roty(0.002*180/pi)*rotz(0.003*180/pi)
% 输出:
delta1 = 3×3
1.0000 -0.0030 0.0020
0.0030 1.0000 -0.0010
-0.0020 0.0010 1.0000
%%交换一下顺序看看:
delta2 = roty(0.002*180/pi)*rotx((0.001*180/pi)*rotz(0.003*180/pi))
% 输出:
delta2 = 3×3
1.0000 -0.0030 0.0020
0.0030 1.0000 -0.0010
-0.0020 0.0010 1.0000
% 我们使用上面推导的公式,就能算出矩阵对应的微小旋转角0.001,0.002,0.003.
vex(delta1 - eye(3,3))'
% 输出:
ans = 1×3
0.0010 0.0020 0.0030
对于两个差异极小的位姿ξ0,ξ1,可以用一个六维向量来表示差异:
由位移增量和旋转增量组成;这个差异δ很明显可以用空间速度✖δt来计算,这个空间速度将在后面《速度关系》这一部分来学习。现在我们考虑位姿用齐次变换矩阵的形式表示:
工具箱中可以用tr2delta求解T。
我们考虑一下上上个公式(3.9)的逆运算:
逆运算可以用delta2tr求解。
matlab实现
% 我们先来确定始末姿态T0,T1
T0 = transl(1,2,3)*trotx(1*180/pi)*troty(1*180/pi)*trotz(1*180/pi);
T1 = T0 * transl(0.01,0.02,0.03)*trotx(0.001)*troty(0.002)*trotz(0.003)
% 输出:
T1 = 4×4
0.2889 -0.4547 0.8425 1.0191
0.8372 -0.3069 -0.4527 1.9887
0.4644 0.8361 0.2920 3.0301
0 0 0 1.0000
% (3.10)中▲的计算是由tr2delta完成的
d = tr2delta(T0, T1);
d' % 转置而已
% 输出:
ans = 1×6
0.0100 0.0200 0.0300 0.0010 0.0020 0.0030
%% 我们尝试一下逆变换,用齐次变换作用于T0,看一看得到的结果与设定末姿态T1的差别
delta2tr(d)*T0
ans = 4×4
0.2903 -0.4521 0.8434 1.0100
0.8376 -0.3061 -0.4524 2.0200
0.4627 0.8378 0.2898 3.0300
0 0 0 1.0000
% 看起来十分接近,误差来源于位移量不是无穷小。
有关tr2delta和delta2tr的解释:
tr2delta:
d = tr2delta(T0, T1)将齐次变换转换为差分运动(差分是离散化的微分),描述从姿态 T0 到 T1 的无穷小变化。将会输出一个六维向量d =(dx, dy, dz, dRx, dRy, dRz),是平均空间速度乘以时间的近似值。
delta2tr:
将差分运动转换为齐次变换。
02-3 惯性导航
我感觉这一部分可以单出一部分来讲,毕竟《惯性导航》可以单独出书来讲的。这里就仅仅作为了解。
惯性导航系统是一个“黑匣子”,由一台计算机和运动传感器组成,输入加速度、角速度等自身测量值,经过运算得到相对于惯性参考系(宇宙)的速度、方向、位置等位姿。
无需外部信号输入,所以它非常适合用于潜艇、航天器和弹道导弹。
- 与其原理相近的是内耳中起平衡作用的传感器。
- 集成了各种传感器的系统叫做惯性测量单元IMU
- 早期惯导和现代捷联式惯导设计原理稍有不同
- 基本思想就是基于惯导系统的高工作采样频率,得到角速度、加速度等进行积分计算,得到速度、位置、角度变化等等,来确定当前位姿。
03 简单总结 | Review
效仿第一部分,通过本部分的学习,我们也需要总结出几个宏观的印象,以便于后续的深入学习:
- 创建机器人运动的轨迹,轨迹的重要特点是光滑,时间和姿态要随时间连续变化。
- 旋转的速度研究,我们研究正交旋转矩阵关于时间导数,我们建立了与力学的角速度速度的联系
- 作为本部分知识的应用,惯性导航中旋转插值和角速度积分都用到正交旋转矩阵法和四元数法。两种方法的结果等价。但四元数法的公式更简洁,计算更有效。


 机器人学继续学习,惯性导航这一块就看了个大概思想,这一部分还是相当硬的。涉及了很多微积分、矩阵变换的基础知识。
机器人学继续学习,惯性导航这一块就看了个大概思想,这一部分还是相当硬的。涉及了很多微积分、矩阵变换的基础知识。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号