编程训练_求和公式
问题描述：
QQ小方以前不会用 excel 里的求和公式，现在他会了，所以他急切的想教会你。 对于 excel 中的一个子矩阵求和的公式格式是 sum(A:B) ，其中 A 表示子矩阵的左上角坐标， B 表示子矩阵的右下角坐标。
单单讲给你听肯定是不够的，为了表现自己，QQ小方现在要考考你。 现在QQ小方会给你一个 n×n 的正方形矩阵，并且它会将正方形矩阵的两条对角线位置全部填上 1 （可以参考下图），其余位置全部填上 0 。并且他给正方形矩阵的行和列从 0 到 n−1 标上了序号。 例如下图所示是 4×4 正方形矩阵的填充和行列标号：
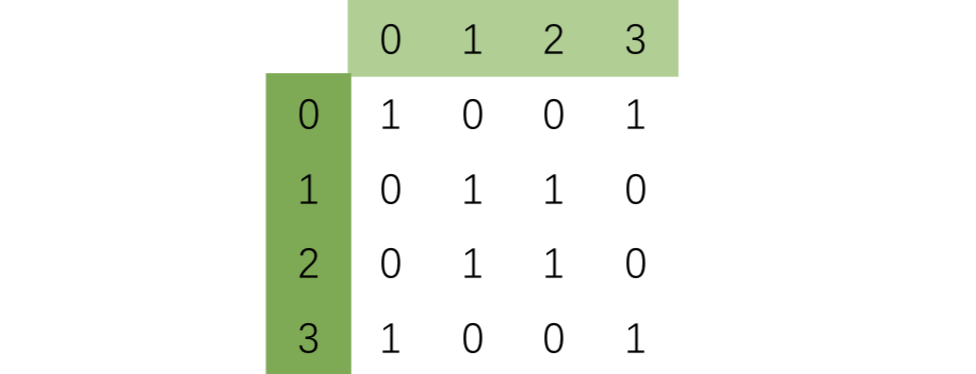
现在，为了测试你是否真的掌握了 excel 的矩阵求和公式，QQ小方会进行 q 次询问，每次询问一个子矩阵的和。 输入格式 输入第一行包含两个整数 n,q(1≤n≤10^18,1≤q≤10^5) ，分别表示矩阵的大小和询问的次数。 接下来的 q 行，每行包含四个整数 a,b,c,d(0≤a≤c<n,0≤b≤d<n) ，表示子矩阵。其中子矩阵的左上角坐标为 (a,b) ，右下角坐标为 (c,d) 。 输出格式 输出包含 q 行，针对每一个询问输出一个整数表示答案。 样例 input 4 2 0 1 1 3 0 0 3 3 output 3 8
题目求解：
1.题目大意转化为一个矩形包含离散直线 y=x 和 y=n-x-1 点的个数问题。
2.值得注意的是包含的点数目可能为0，且矩阵的范围是10^18，如果使用循环遍历的话，很可能会超时。
3.下面对直线y=x 求包含点的个数，即在X轴上的投影，通过绘图可以得出如下结论
(1). 与 y=x 相交的点有 (a,a),(b,b),(c,c),(d,d),而且落在矩形边界的点在X轴上投影为 max(a,b),min(c,d);
(2). 与 y=x 无交点的判别式：(b-c)*(d-a)>0
分析：若矩形与直线 y=x 无交点，则矩形处在直线的上方或者下方，即 (b-c)与(d-a)同号，即(b-c)*(d-a)>0;
(3). 对于直线 y=x 求交点个数
// 当在直线 y=x 异侧时有交点
if ((b-c)*(d-a)<=0)
sum_i = sum(max(a,b),min(c,d));
// 其中sum(int m, int n) 函数的计算方式为
// abs(n-m)+1;
4.下面对直线y=n-x-1 求包含点的个数，方法同3
(1). 与 y=n-x-1 相交的点有 (a,n-1-a),(b,n-1-b),(n-1-c,c),(d,n-1-d),而且落在矩形边界的点在X轴上投影为 max(b,n-1-c),min(n-1-a,d);
(2). 与 y=n-x-1 无交点的判别式：(a+b+1-n)*(c+d+1-n)>0
分析：若矩形与直线 y=n-x-1 无交点，则矩形处在直线的上方或者下方，即 (a+b+1-n)与(c+d+1-n)同号，即(a+b+1-n)*(c+d+1-n)>0;
(3). 对于直线 y=n-x-1 求交点个数
// 当在直线 y=n-x-1 异侧时有交点
if ((a+b+1-n)*(c+d+1-n)<=0)
sum_j = sum(max(b,n-1-c),min(d,n-1-a));
5. 讨论两条直线存在重复值的情况
(1). 由于该直线表达形式为连续直线，则当n为奇数时，会存在中心交点重合的情况;
(2). 此情况下该点有可能计算两次，应该去重
if (n%2 == 1)
if (a<=n/2 && c>=n/2 && b<=n/2 && d>=n/2)
flag = 1;
问题反思：
1.该矩阵的阶次达到 10^18，尽量避免循环遍历；
2.判断矩形是否与直线相交时，应避免整数相乘再判断符号；
// 1. y=x // 最好不要采用乘积为非正的算式，当数很大的时候会报错 if (b>=c&&d<=a || b<=c&&d>=a) sum_i = sum(max(a,b),min(c,d)); // 2. y=n-x+1 if (b>=(n-1-a)&&d<=(n-1-c) || b<=(n-1-a)&&d>=(n-1-c)) sum_j = sum(max(b,n-1-c),min(n-1-a,d));
3.使用求和函数时为了保证结果为正，也应避免使用abs()函数，因为精度会降低，从而导致报错；
long long sum(long long a, long long b)
{
// printf("abs sum = %lld\n",abs(a-b+1));
// printf("sum = %lld\n",(a>b?a-b+1:b-a+1));
// 上述两式的结果不同
return a>b?a-b+1:b-a+1;
}
4.不要忘记n为奇数时的去重处理。
if (n%2 == 1)
if (a<=n/2 && c>=n/2 && b<=n/2 && d>=n/2)
flag = 1;
printf("%lld\n",sum_i+sum_j-flag);
AC代码：
# include <stdio.h>
# include <math.h>
long long max(long long a, long long b)
{
return a>b?a:b;
}
long long min(long long a, long long b)
{
return a>b?b:a;
}
long long sum(long long a, long long b)
{
return a>b?a-b+1:b-a+1;
}
int main(void)
{
long long n, sum_i, sum_j, flag = 0;
int q;
long long a, b, c, d;
scanf("%lld %d",&n, &q);
while (q>0)
{
flag = 0;
sum_i = sum_j = 0;
scanf("%lld %lld %lld %lld",&a,&b,&c,&d);
// 分两条线计算，求交点坐标，然后计算包含的点个数
// 1. y=x
// 最好不要采用乘积为非正的算式，当数很大的时候会报错
if (b>=c&&d<=a || b<=c&&d>=a)
sum_i = sum(max(a,b),min(c,d));
// 2. y=n-x+1
if (b>=(n-1-a)&&d<=(n-1-c) || b<=(n-1-a)&&d>=(n-1-c))
sum_j = sum(max(b,n-1-c),min(n-1-a,d));
q--;
if (n%2 == 1)
if (a<=n/2 && c>=n/2 && b<=n/2 && d>=n/2)
flag = 1;
printf("%lld\n",sum_i+sum_j-flag);
}
return 0;
}
RRR
