基本排序算法之堆排序

基础知识

1991年计算机先驱奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德(Robert W．Floyd）和威廉姆斯(J．Williams）在1964年共同发明了著名的堆排序算法（Heap Sort )。（二叉）堆数据结构是一种数据对象，它可以被视为一棵完全二叉树，树中每个节点与数组中存放该节点的那个元素对应，树的每一层都是填满的，最后一层可能除外（最后一层从最左边节点的左子树开始填。堆氛围两种：最大堆（大根堆）和最小堆（小跟堆）。一个最大堆可以看成一棵完全二叉树和一个数组（见图一），圆圈中的数字表示书中每个节点存储的值，及诶单那上方的数字表示对应的数组下标。图一中树的高度为小堆的组织方式与最大堆恰好相仿。使得在当前无序区中选取最大（或最小）关键字的记录变得简单。

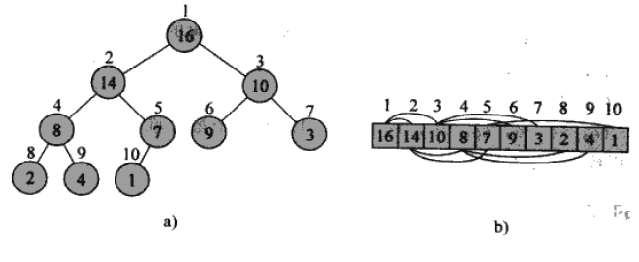
图一

算法理解

算法主要分为两个过程：建堆和堆排序。图二是建堆过程，图三是堆排序过程。

图二

 

 

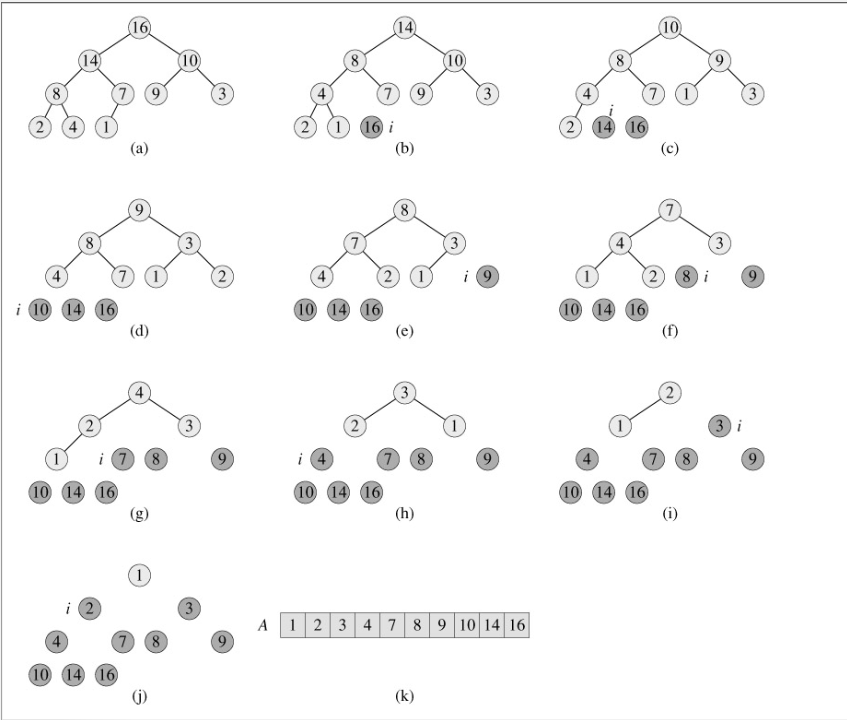
图三

 

Java代码

 

package chap06;

public class HeapSort {

    private int[] waitForSortedArray;
    private int heapSize;

    public HeapSort(int[] IntArray) {
        this.waitForSortedArray = IntArray;
        this.heapSize = this.waitForSortedArray.length - 1;
    }

    /* return left child index */
    public int getLeftChild(int parentIndex) {
        return parentIndex * 2 + 1;
    }

    /* return right child index */
    public int getRightChild(int parentIndex) {
        return parentIndex * 2 + 2;
    }

    /* exchange two number in Array */
    public void swap(int array[], int index1, int index2) {
        int tempNum = 0;
        tempNum = array[index1];
        array[index1] = array[index2];
        array[index2] = tempNum;
    }
    
    /* output the result of array sorted */
    public void outputSortedResult() {
        for(int i = 0;i < waitForSortedArray.length ; i++){
            System.out.println(waitForSortedArray[i]);
        }
    }
    
    /* Adjust the heap to meet the max heap property */
    public void MAX_HEAPIFY(int[] A, int index) {
        int lIndex = getLeftChild(index);
        int rIndex = getRightChild(index);
        int largest = 0;
        if (lIndex <= heapSize && A[lIndex] > A[index]) {
            largest = lIndex;
        } else {
            largest = index;
        }
        if (rIndex <= heapSize && A[rIndex] > A[largest]) {
            largest = rIndex;
        }

        if (largest != index) {
            swap(A, largest, index);
            MAX_HEAPIFY(A, largest);
        }
    }

    /* build heap */
    public void BUILD_MAX_HEAP(int[] A) {
        int tmp = heapSize / 2;
        for (int i = tmp; i >= 0; i--) {
            MAX_HEAPIFY(A, i);
        }
    }

    /* heap sort */
    public void HEAPSORT(int[] A) {

        BUILD_MAX_HEAP(A);
        for (int i = heapSize; i >= 1; i--) {
            swap(A, 0, i);
            heapSize = heapSize - 1;
            MAX_HEAPIFY(A, 0);
        }
    }

    public static void main(String[] args) {
         int [] array = {5,3,1,7,9,11, 13, 2};
         HeapSort test = new HeapSort(array);
         test.HEAPSORT(array);
         test.outputSortedResult();
    }
}