计概大作业之同化棋

前言：

　　唔，进了大学很久没有更新博客了...感觉自己的语言能力和代码理解能力也随着不写博客有一定的下降...

　　最近看到室友们的计概大作业，同化棋AI。觉得挺有意思，于是也想着试一试，同时开一篇博客来记录自己思考的过程。

 

STEP1

　　首先我们需要对同化棋有一定的了解

　　初始布置为双方各将两枚棋子放在最外的对角格。

　　玩家必须轮流移动一枚己子到一个空棋位，该棋位可以是邻近八格（包括对角相邻的格）之一，或相隔一格的次邻十六格之一。移动的新棋位，会使邻近的所有敌棋如黑白棋一样变成己方。如果棋子移到的是邻接八格，会有一颗新己棋出现在原先棋位。

　　无法行棋需弃权[就输了]。当两方都无法行棋时，游戏结束。以最多子者胜。

　　

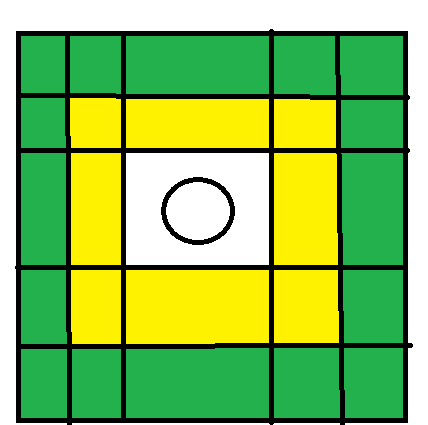
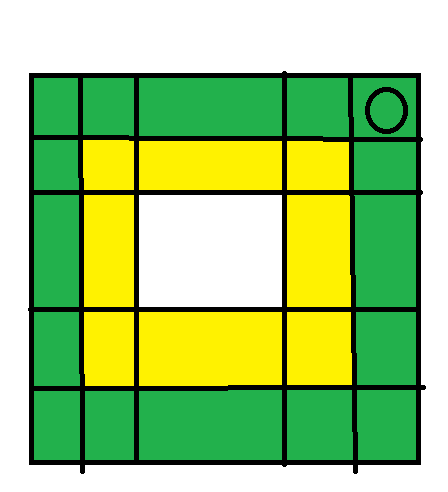
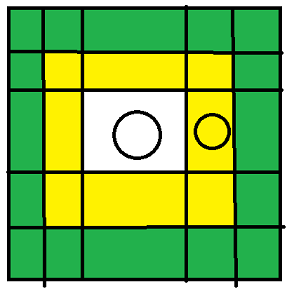
　　其中黄色和绿色都是可以移动的位置，但是如果移动到绿色，原本中间的棋子会消失，而如果在黄色区域，原本中间的棋子不会消失

　　而后面的变颜色说的邻近，也是黄色区域部分的所有棋子会变成放入中间的棋子的颜色。

 

了解完了规则，那么我们就可以利用程序实现棋盘的基本操作了

STEP2

　　支持的操作有：选中一个棋子，移动到一个位置，移动后的变化。

　　棋盘显然的，最容易想到使用二维数组模拟。

　　1.选中一个棋子：考虑到目前只能使用控制台，那么我们可能需要输入棋子的行和列，那么考虑到视觉感受，我们需要把棋盘也输出。【怎么输入一个优美的棋盘？】

　　　　　　　　　　在这个操作时，需要考虑这个位置是不是自己可以操作的棋子。

　　2.移动到一个位置：需要判断移动的合法性，那么就是abs(x1-x2)<=2 abs(y1-y2)<=2，以及移动到的位置是否在棋盘内，是否为空地

　　3.移动后的基本变化：首先需要考虑移动距离，是在黄色区域还是绿色区域，这样来考虑是否复制，然后将周围有棋子的地方都染上自己的颜色。

　　如何判断游戏是不是结束了呢？

　　1.棋盘放慢了比谁棋子多

　　2.某一方没有子或者没有可以移动的子了算输

　　这样就需要一个统计棋子数目的函数和一个判断点是否能走的函数。

　　嗯嗯，这里可以提一下判断是否能走的时候，我们很容易想到以前的跳马问题类似的搜索，需要建立move_x[]和move_y[]数组，而这个题也可以这样做，但是总共有24步，便可以使用for循环来初始化了...（同样还有染色需要周围的移动，也可以通过这个方法）

　　这里便是整个程序的初始化过程

void init(){
    map[1][7]=map[7][1]=1;
    map[1][1]=map[7][7]=2;
    int tmp=0;
    for(int i=-2;i<=2;i++)
        for(int j=-2;j<=2;j++)
            if(!(i==0 && j==0)) tmp++,mvx[tmp]=i,mvy[tmp]=j; //mvx和mvy分别表示棋子移动时x方向上和y方向上的移动 
    tmp=0;
    for(int i=-1;i<=1;i++)
        for(int j=-1;j<=1;j++)
            if(!(i==0 && j==0)) tmp++,arx[tmp]=i,ary[tmp]=j; //arx和ary分别表示染色时在x和y上的移动 
}

 

　　设计一个程序打出棋盘也是十分容易的。当然为了美观性，我可以来介绍一下如何输出一个优美的棋盘。

　　【如何输出一个优美的棋盘】

　　.一开始我觉得这个没有什么关系...这是我的【棋盘1.0】

　　

　　你看还是挺好看的吗...良心的加上了你和电脑的棋子数目，而且 @ 和 # 显然是OI里画图经常使用的符号嘛...

　　唔，当然控制台上看这个就丑陋了...

　　

　　

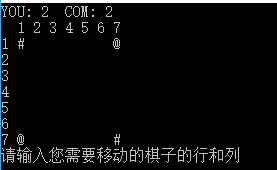
　　当时室友说你这个太丑了...他们的助教居然想到了使用制表符...唔，可是不知道制表符的编码方式怎么办呢？

　　哈，直接使用字符串...然后在word里找出这个制表符来复制就可以了！

　　

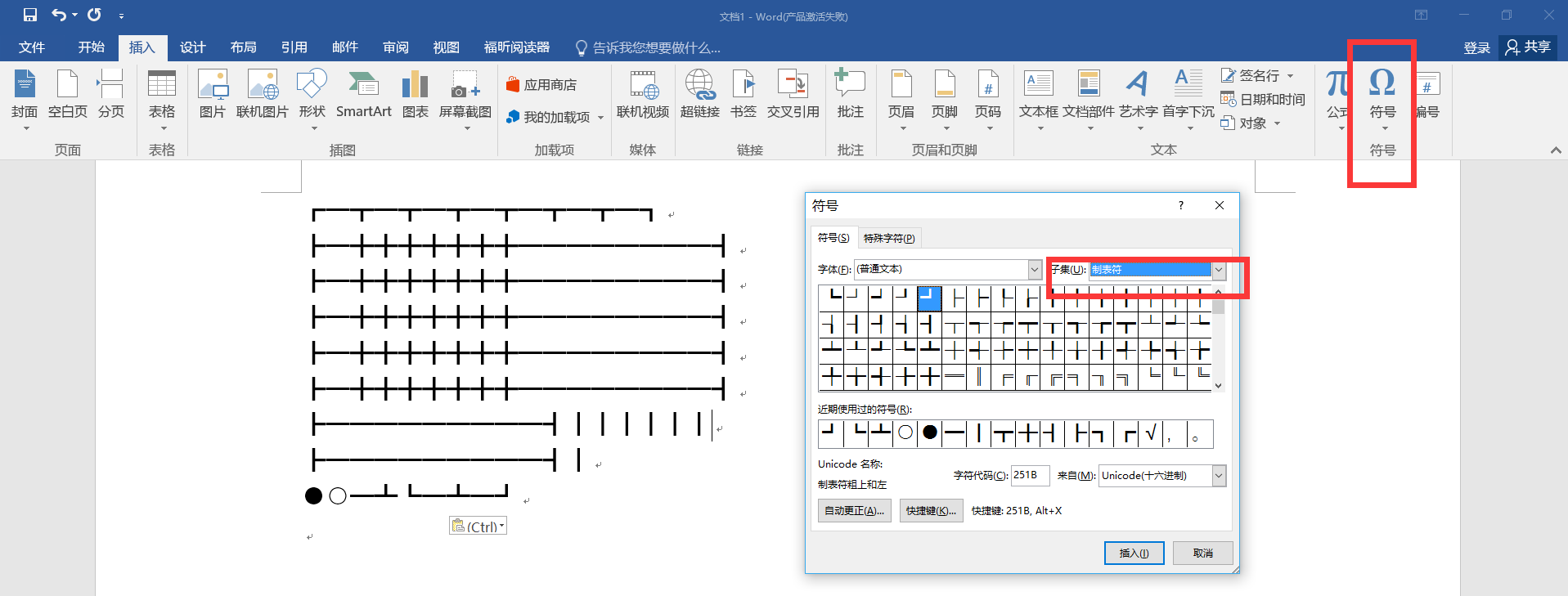
　　好了这是我的word寻找过程...然后选定了两个棋子——黑圈和白圈( 这两个好像就在制表符下面一点点就能找到 )

　　哇，简直良心制作人...

　　然后就诞生了我的【棋盘2.0】

　　

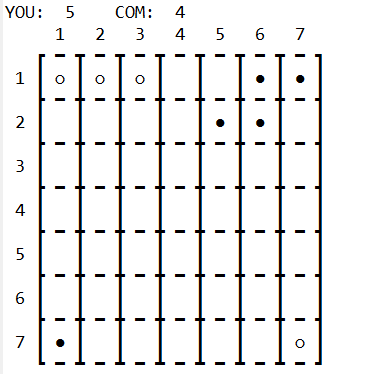
　　dev文本效果还不错的呢...当然最重要的是看控制台效果！（因为毕竟得在控制台下棋）

　　

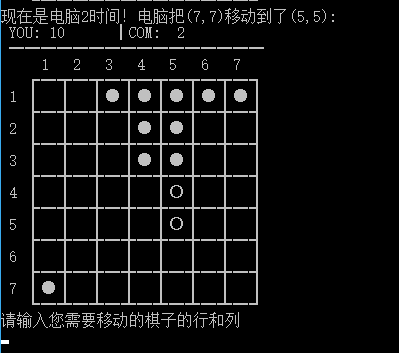
　　有没有觉得十分好看！（相比之前那个hhh）顺便mark一发我的贪心算法被我无情打败的过程...

void print2(int map[][9]){
    sum(map);
    printf(" YOU: %2d      ┃COM: %2d\n",cnt[1],cnt[2]);
    printf(" ━━━━━━━━━━━━━━━━ \n"); 
    printf("     1   2   3   4   5   6   7  \n");
    printf("   ┏━┳━┳━┳━┳━┳━┳━┓\n");
    printf(" 1 ┃");
    for(int i=1;i<=7;i++)
        if(map[1][i]==1) printf("●┃");
        else if(map[1][i]==2) printf("○┃");
        else printf("  ┃");
    putchar('\n');
    for(int i=2;i<=7;i++){
        printf("   ┣━╋━╋━╋━╋━╋━╋━┫\n");
        printf(" %d ┃",i);
        for(int j=1;j<=7;j++)
            if(map[i][j]==1) printf("●┃");
            else if(map[i][j]==2) printf("○┃");
            else printf("  ┃");
        putchar('\n');
    }
    printf("   ┗━┻━┻━┻━┻━┻━┻━┛\n");
}

　　上面便是写的代码，可以先画出来再写成for循环的棋盘模式

 STEP3

　　既然要做一个良心游戏，那么还需要一个游戏界面：例如新游戏和存档之类的...

　　新游戏还是十分简单的，比较麻烦的有返回上层和读取存档。

　　【返回上层】因为我写的界面比较简陋，而且我相信玩家不会调戏游戏界面，所以如果返回上层我直接再次调用一次就可以了...

　　【读取、存储档】因为我们的输入是在控制台的，那么我们存档又是一个文件操作，那么我们可以使用fscanf和fprintf的操作。

　　　　那么这两个的基本使用方法和scanf()和print()几乎一样，只是他们需要一个文件指针FILE *fp;

　　　　当输入的时候定义文件指针FILE *fp=fopen("rec.txt","r");

　　　　使用的时候fsanf(fp,"%d",&a);就可以啦...输出也类似咯，那么每次存档就在文件里输出当前棋盘，读取就在文件里输入棋盘就可以啦...

 

STEP4

　　现在就是激动人心的AI时刻：

　　【贪心的思想】

　　当然，一开始我是没有思路的，一开始跟手机上的app下的时候就会被吊起来打...唔，因为我使用的就是一步贪心，贪心能吃的子最多...至于这个子最多这种...有类似的自己的子最多、别人的子最少、以及自己的子减去别人的子最多等等等...

　　这样的简单贪心就不用说了...其实经过我后来下了很多次之后，我发现，每次如果我能跳进一个矩形中，那么我的收益非常大，而且别人一时间吞不掉我的，唔，抱着这种简陋的想法，我打了一个贪心目的是能在我走了一步之后判断我的棋子形成的最大矩阵能不能更大，就是在吃子相同的前提下进行第二步的关于最大矩阵面积的判断。

　　再后来我还发现了基本上每次我赢的时候，棋盘中我几乎所有的棋子都是联通的 (只有角落上的几个散落在旁边)，那么是不是可以用最大联通块来进行贪心呢？不过我就没有尝试了哈...因为我已经巧妙的想到了一种方法吊打自己的贪心AI...

　　然后不讨论一步贪心了，很容易的我们会想到两步贪心，即希望我走完一步之后，对手也走完一步之后，我的棋子还是占据优势的，那么自然也会有三步贪心等等等等....

　　【搜索的思想】

　　我感觉搜索的思想也就从贪心的几步贪心这里诞生了...

　　既然我能一直判断到很多步之后的事情，那么我们是不是可以就直接搜索呢？当然想要搜索是要先挖掘很多性质的。

　　首先，很重要的一点，我之前是怎么走的已经不重要了，决定我下一步怎么走的就是当前的棋盘。

　　那么现在的搜索就应该是一棵树，棋盘记录了一个状态，而状态又会通过走来形成新的状态，与其他树不一样的是，这种拓展有两种拓展，分为我的选择和对手的选择，因为它们扩张的棋子不一样，目的也不一样。

　　这里便会涉及到一个博弈树的概念。同时呢，也会涉及到一个经典Minimax算法，同时在这个算法研究的问题上也很容易用到一个叫做alpha-beta剪枝的算法...

　　幸运的发现了两个比较好理解的博客：

　　介绍Minimax算法的：https://www.cnblogs.com/zhuli19901106/p/3832592.html

　　介绍alpha-beta剪枝的：http://blog.csdn.net/baixiaozhe/article/details/51872495

　　我也用自己的话来讲讲自己理解的这两个算法吧：

　　Minimax比较好理解，就是双方分别希望自己的值最大、希望对方的值最小。在这个算法中，只有一方会得分，这一方希望自己的利益最大，而另一方的决策会希望这一方得分越少越好。

　　那么我们来讨论一个节点的后继是怎么影响这一点的：

　　如果这个节点是希望得分者的点，那么这个点的最小得分应该是会因为寻找更多的后继而不减的。【这里之所以称作最小得分是假设后面还不知道的情况，所以如果我只通过现在已知的这些点得到的目前最大值应该是理论上的一个下界】，那么我的下界会因为更多后继的搜寻而慢慢变大(或者不变)

　　反过来，如果这个点是阻碍得分方的节点，那么这个点的上界应该会因为寻找更多的后继而不增的。也就是随着搜索的后继更多我更容易选到一个更差的解。

　　那么alpha-beta剪枝算法就是建立在这个上面的。

　　我们还要对刚才的想法再往下思考一层。

　　从希望得分者的角度出发：我的后继我是希望找到一个比当前值更大的后继的，对吗？

　　但是我的后继是由阻碍者来进行的，也就是说，我的后继如果还没有搜完就得到了一个比当前最优值要小或者相等的值，根据阻碍者的行动，如果想要完善这个后继的话，只会让我的后继的上界越来越小，但是即使是当前的上界已经到达我的下界了，所以就没有必要完善这个后继了，因为我一定不会采用的。【忽然想到一个成语叫：“断子绝孙”：因为我们的操作就是：断掉这个儿子，停止这个儿子继续延展出孙子】这样就达到了减少搜索量的目的，是一个很有效的剪枝。

　　那么，从这个理论上的东西还要和我们的同化棋结合起来，分析这种算法的可行性。而这就是我们最艰巨的任务了。

 

　　首先，整个搜索的主体是这一棵博弈树。我们应该想办法把整个博弈树的实现弄清楚。

　　先假定我是希望得分者，那么在我这一层便是白琪移动，在我的下一层是黑棋移动。

　　为了使用我们的剪枝，我们让这个博弈树深度优先生长。

　　而通过移动产生的后继，为了测试复杂度需要进行一个估算：假设当前移动的子有n枚，剩余的空地<=48-n。那么粗略的估算的话：应该是<=n*(48-n)<=24*24=576，当然这种当前子碾压另一种颜色的子的数目是很少出现的，希望的情况是两种棋子差别不要太大，我打了一个程序：随机10000个局面算后继平均值，算了大约有10次，都发现后继在(87,89)的这个区间。【下面是我测试用的代码】

#include<cstdio>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>

using namespace std;

int ans;
int map[9][9],rec[9][9];
int mvx[25],mvy[25];
int move_list[25],top;
//初始化函数 
void init(){
    int tmp=0;
    for(int i=-2;i<=2;i++)
        for(int j=-2;j<=2;j++)
            if(!(i==0 && j==0)) tmp++,mvx[tmp]=i,mvy[tmp]=j; //mvx和mvy分别表示棋子移动时x方向上和y方向上的移动 
}

int can_move(int x,int y){
    top=0;
    int nx,ny;
    for(int i=1;i<=24;i++){
        nx=x+mvx[i],ny=y+mvy[i];
        if(nx>=1 && nx<=7 && ny>=1 && ny<=7 && !map[nx][ny])
            move_list[++top]=i;
    }
    return top;
}

int count(){
    int cnt=0,t=0;
    for(int i=1;i<=7;i++)
        for(int j=1;j<=7;j++)
            if(map[i][j]==2) cnt+=can_move(i,j);
            else if(map[i][j]==1) t=1;
    return cnt;
}

void random_map(){
    for(int i=1;i<=7;i++)
        for(int j=1;j<=7;j++)
            map[i][j]=rand()%3;
}

int main(){
    freopen("test2.out","w",stdout);
    long long sum=0;
    init();
    srand(time(0));
    for(int K=1;K<=10000;K++){
        random_map(); 
        sum+=count();
    }
    printf("%lf",sum/10000.0);
    return 0;
}

　　当然笔者平时下棋的时候发现每次其实能走的只有6步左右，当然是经过了肉眼贪心了之后[例如如果一个地方能复制过去，我就不跳过去]，所以说事实上当我们的树往下探的时候，期望的剪枝后继会只剩下6左右。但是我们的alpha-beta剪枝是一个剪孙子的算法，也就是期待的只能把儿子的后继变成一个很小的数，但是儿子的数目也是比较多的，这里我们就要考虑先搜哪些儿子更容易找到一个更好的解了。

　　笔者目前的想法是：1、先用一次多步贪心得到一个局部最优，再使用alpha-beta剪枝算法来剪枝。【这样的复杂度会有些大，但是我们控制层数的话因为和后面的算法是一个加法关系应该是很有可行性的】

　　　　　　　　　　　2、希望儿子的拓展顺序能够有一个一层的小贪心来决定顺序。也就是走了一步之后得到的子的数目排个序。这样的操作是一个nlogn的复杂度而且是加法，我觉得会是十分有效的。【或者优化2其实可能会悄悄地实现了优化1？】

　　

　　然后上面其实一直忽略掉了一个东西，就是博弈树上每个节点的利益，也就是我需要一个估价函数来判断哪个棋盘好，哪个棋盘不好。这样我们才能确定后继的上界和下界。

　　但是这个估价函数却不能单纯的凭借哪一方的子多来判断。它和棋子占据的位置也有着密切的关系。在这里我还是没有想放弃我的最大矩阵的判断，我认为矩阵是一种防御的姿态，因为只要的你的矩阵>=2*2无论对方怎么吞，得到你的棋子数都是<=3的。当然还有行动力也是一个棋盘升值的筹码，如果行动力大，那么后继多，好的机会也会多。那这些参数之间是一个怎样的组合？我觉得是十分复杂的。

 

　　....嗯嗯，我打了一个简单的弃坑啦...

　　因为明年我才选这个课hhh，死亡。

　　我在打程序的过程中，还发现了递归的特点，就是如果我要存一个棋盘的话，不一定要放在函数中定义，你可以按照层来分，然后放在全局变量中，因为使用深搜时，每一层在同时间最多只会出现一个，而且不管你在一个函数中调用几次别的函数，每一层也最多只有一个。这样下来我又想到了，为什么我们的程序会存在一个栈空间里。好吧，我一定是最后想这个问题的人....

　　最后附上我的代码...大家不要抄哦

　　

/*
    Author : Robert_Yuan
*/

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int INF=0x3f3f3f3f;

int map[9][9],TTT[9][9];
int cnt[3];
int mvx[25],mvy[25];
int arx[9],ary[9];
int move_list[25],top;

void init();//初始化 
void menu();//操作界面 
void sum();//统计棋子数目 
void print(int map[][9]);//输出棋盘 
void print2(int map[][9]);//输出一个好看的棋盘 
void operation1();//单人游戏 
void operation2();//双人游戏 
void Copy();
void Save1();//存单人游戏档 
void Save2();//存双人游戏档 
bool can_move(int x,int y);
void Search1(int Depth);
void Search2(int Depth);

int main(){
    //freopen("bug.in","r",stdin);
    //freopen("game.out","w",stdout); 
//    init();
    menu();
    //operation1();
} 

void menu(){
    int ord1,ord2;
    printf(" ━━━━━━━━━━━━━━━━━━━━━━━━ \n"); 
    printf("欢迎来到同化棋小游戏，您可以输入数字来进行以下操作\n");
    printf(" ━━━━━━━━━━━━━━━━━━━━━━━━\n"); 
    printf("    0.退出游戏\n");
    printf("    1.单人游戏\n");
    printf("    2.双人游戏\n");
    scanf("%d",&ord1);
    if(ord1==1){
        printf("     ━━━━━━━━━━━━━━━━━━━━━━━\n"); 
        printf("    您来到了单人游戏，您可以输入数字来进行以下操作\n");
        printf("     ━━━━━━━━━━━━━━━━━━━━━━━\n"); 
        printf("        0.返回上层\n");
        printf("        1.新游戏\n");
        printf("        2.读取存档\n");
        scanf("%d",&ord2); 
        if(ord2==0) menu();//返回上层即再次递归 
        else{
            init();
            if(ord2==2){//读取存档 
                FILE *fp;
                fp=fopen("rec1.txt","r");
                for(int i=1;i<=7;i++)
                    for(int j=1;j<=7;j++)
                        fscanf(fp,"%d",&map[i][j]);
            }
            operation1();
        } 
    }
    else if(ord1==2){
        printf("     ━━━━━━━━━━━━━━━━━━━━━━━\n"); 
        printf("    您来到了双人游戏，您可以输入数字来进行以下操作\n");
        printf("     ━━━━━━━━━━━━━━━━━━━━━━━\n"); 
        printf("        0.返回上层\n");
        printf("        1.新游戏\n");
        printf("        2.读取存档\n");
        scanf("%d",&ord2);
        if(ord2==0) menu();
        else{
            init();
            if(ord2==2){
                FILE *fp;
                fp=fopen("rec2.txt","r");
                for(int i=1;i<=7;i++)
                    for(int j=1;j<=7;j++)
                        fscanf(fp,"%d",&map[i][j]);
            }
            operation2();
        } 
    }
    else 
        return ;
}

//初始化函数 
void init(){
    //初始化棋盘 
    map[1][7]=map[7][1]=1;
    map[1][1]=map[7][7]=2;
    //初始化移动和周围数组 
    int tmp=0;
    for(int i=-2;i<=2;i++)
        for(int j=-2;j<=2;j++)
            if(!(i==0 && j==0)) tmp++,mvx[tmp]=i,mvy[tmp]=j; //mvx和mvy分别表示棋子移动时x方向上和y方向上的移动 
    tmp=0;
    for(int i=-1;i<=1;i++)
        for(int j=-1;j<=1;j++)
            if(!(i==0 && j==0)) tmp++,arx[tmp]=i,ary[tmp]=j; //arx和ary分别表示染色时在x和y上的移动 
}

//统计棋盘内各种子的数目 
void sum(int map[][9]){
    cnt[0]=cnt[1]=cnt[2]=0;
    for(int i=1;i<=7;i++)
        for(int j=1;j<=7;j++)
            cnt[map[i][j]]++;
}

//输出一个简陋的棋盘(@和#组成) 
void print(int map[][9]){
    sum(map);
    printf("YOU:%2d  COM:%2d\n",cnt[1],cnt[2]); 
    putchar(' ');
    for(int i=1;i<=7;i++)
        printf(" %d",i);
    putchar('\n');
    for(int i=1;i<=7;i++){
        printf("%d",i);
        for(int j=1;j<=7;j++){
            if(map[i][j]==1) printf(" @");
            else if(map[i][j]==2) printf(" #");
            else printf("  ");
        }
        putchar('\n');
    }
}

//输出一个漂亮的棋盘，使用制表符 
void print2(int map[][9]){
    sum(map);
    printf(" ━━━━━━━━━━━━━━━━ \n"); 
    printf(" YOU: %2d      ┃COM: %2d\n",cnt[1],cnt[2]);
    printf(" ━━━━━━━━━━━━━━━━ \n"); 
    printf("     1   2   3   4   5   6   7  \n");
    printf("   ┏━┳━┳━┳━┳━┳━┳━┓\n");
    printf(" 1 ┃");
    for(int i=1;i<=7;i++)
        if(map[1][i]==1) printf("●┃");
        else if(map[1][i]==2) printf("○┃");
        else printf("  ┃");
    putchar('\n');
    for(int i=2;i<=7;i++){
        printf("   ┣━╋━╋━╋━╋━╋━╋━┫\n");
        printf(" %d ┃",i);
        for(int j=1;j<=7;j++)
            if(map[i][j]==1) printf("●┃");
            else if(map[i][j]==2) printf("○┃");
            else printf("  ┃");
        putchar('\n');
    }
    printf("   ┗━┻━┻━┻━┻━┻━┻━┛\n");
}

//判断一个位置的琪是否还有位置可以移动 ，同时将可以移动的方向存在move_list中 
bool can_move(int x,int y){
    top=0;
    int nx,ny;
    for(int i=1;i<=24;i++){
        nx=x+mvx[i],ny=y+mvy[i];
        if(nx>=1 && nx<=7 && ny>=1 && ny<=7 && map[nx][ny]==0)
            move_list[++top]=i;
    }
    return top!=0;
}

//处理一个从(x1,y1)移动到(x2,y2)的t种棋子所产生的效果 
void Deal_With(int x1,int y1,int x2,int y2,int t,int map[][9]){
    map[x1][y1]=t*(abs(x2-x1)<=1 && abs(y2-y1)<=1);
    map[x2][y2]=t;
    int nx,ny;
    for(int i=1;i<=8;i++){
        nx=x2+arx[i],ny=y2+ary[i];
        if(map[nx][ny]) map[nx][ny]=t;
    }
}

//单人游戏存档 
void Save1(){
    FILE *fp;
    fp=fopen("rec1.txt","w");
    for(int i=1;i<=7;i++){
        for(int j=1;j<=7;j++)
            fprintf(fp,"%d ",map[i][j]);
        fprintf(fp,"\n");
    }
}

//双人游戏存档 
void Save2(){
    FILE *fp;
    fp=fopen("rec2.txt","w");
    for(int i=1;i<=7;i++){
        for(int j=1;j<=7;j++)
            fprintf(fp,"%d ",map[i][j]);
        fprintf(fp,"\n");
    }
}

//复制两个棋盘 
void Copy(int A[][9],int B[][9]){
    for(int i=1;i<=7;i++)
        for(int j=1;j<=7;j++)
            B[i][j]=A[i][j];
}

//电脑0，使用黑棋子最多战略 
void COMPUTER0(){
    printf("现在是电脑0时间！");
    int BEST_I,BEST_J,BEST_NI,BEST_NJ,BEST=0;
    for(int i=1;i<=7;i++)
        for(int j=1;j<=7;j++)
            if(map[i][j]==2){
                if(can_move(i,j)){
                    for(int k=1;k<=top;k++){
                        int nx=i+mvx[move_list[k]],ny=j+mvy[move_list[k]];
                        Copy(map,TTT);
                        Deal_With(i,j,nx,ny,2,TTT);
                        sum(TTT);
                        if(cnt[2]>BEST)
                            BEST=cnt[2],BEST_I=i,BEST_J=j,BEST_NI=nx,BEST_NJ=ny;
                    }
                }
            }
    Deal_With(BEST_I,BEST_J,BEST_NI,BEST_NJ,2,map);
    printf("电脑把(%d,%d)移动到了(%d,%d):\n",BEST_I,BEST_J,BEST_NI,BEST_NJ);
}

//电脑1，使用黑棋减去白琪最多战略 
void COMPUTER1(){
    printf("现在是电脑1时间！");
    int BEST_I,BEST_J,BEST_NI,BEST_NJ,BEST=-49;
    for(int i=1;i<=7;i++)
        for(int j=1;j<=7;j++)
            if(map[i][j]==2){
                if(can_move(i,j)){
                    for(int k=1;k<=top;k++){
                        int nx=i+mvx[move_list[k]],ny=j+mvy[move_list[k]];
                        Copy(map,TTT);
                        Deal_With(i,j,nx,ny,2,TTT);
                        sum(TTT);
                        if(cnt[2]-cnt[1]>BEST)
                            BEST=cnt[2]-cnt[1],BEST_I=i,BEST_J=j,BEST_NI=nx,BEST_NJ=ny;
                    }
                }
            }
    Deal_With(BEST_I,BEST_J,BEST_NI,BEST_NJ,2,map);
    printf("电脑把(%d,%d)移动到了(%d,%d):\n",BEST_I,BEST_J,BEST_NI,BEST_NJ);
}

int height[9],ins[9],ht;//height和ht表示维护的单调栈和栈顶指针，ins表示每个位置能管到的最前面的位置 
int Left[9][9];//Left表示统计这个位置往左边最长延伸为多少 

//返回两个值中的最大值 
int Max(int x,int y){
    return x>y?x:y;
}

int Min(int x,int y){
    return x<y?x:y;
}

//计算map中t的最大矩阵，使用单调栈 
int calcu_matrix(int map[][9],int t){
    int ans=0;
    for(int i=1;i<=7;i++)
        for(int j=1;j<=7;j++){
            Left[i][j]=0;
            if(map[i][j]==t)
                Left[i][j]=Left[i][j-1]+1;
        }
    for(int i=1;i<=7;i++){
        ht=0;
        for(int j=1;j<=8;j++){
            while(Left[height[ht]][i]>=Left[j][i] && ht>0){
                ans=Max(ans,Left[height[ht]][i]*(j-ins[height[ht]]));
                ht--;
            }
            ins[j]=height[ht]+1;
            ans=Max(Left[j][i]*(j-ins[j]+1),ans);
            height[++ht]=j;
            
        }
    }
    return ans;
}

//COM1优化：当黑子减白子相同时，可以通过最大矩阵进行第二次判断
void COMPUTER2(){ 
    printf("现在是电脑2时间！");
    int BEST_I,BEST_J,BEST_NI,BEST_NJ,BEST=-49,BESTC=0;
    for(int i=1;i<=7;i++)
        for(int j=1;j<=7;j++)
            if(map[i][j]==2){
                if(can_move(i,j)){
                    for(int k=1;k<=top;k++){
                        int nx=i+mvx[move_list[k]],ny=j+mvy[move_list[k]],nc;
                        Copy(map,TTT);
                        Deal_With(i,j,nx,ny,2,TTT);
                        nc=calcu_matrix(TTT,2);
                        sum(TTT);
                        if(cnt[2]-cnt[1]>BEST)
                            BEST=cnt[2]-cnt[1],BEST_I=i,BEST_J=j,BEST_NI=nx,BEST_NJ=ny,BESTC=nc;
                        else if(cnt[2]-cnt[1]==BEST && BESTC<nc){
                            BEST_I=i,BEST_J=j,BEST_NI=nx,BEST_NJ=ny,BESTC=nc;
                        }
                    }
                }
            }
    Deal_With(BEST_I,BEST_J,BEST_NI,BEST_NJ,2,map);
    printf("电脑把(%d,%d)移动到了(%d,%d):\n",BEST_I,BEST_J,BEST_NI,BEST_NJ);
}
int move_steps(int x,int y){
    top=0;
    int nx,ny;
    for(int i=1;i<=24;i++){
        nx=x+mvx[i],ny=y+mvy[i];
        if(nx>=1 && nx<=7 && ny>=1 && ny<=7 && !map[nx][ny]) top++;
    }
    return top;
}

int Move_power(int t){
    int cnt=0;
    for(int i=1;i<=7;i++)
        for(int j=1;j<=7;j++)
            if(map[i][j]==t) cnt+=move_steps(i,j);
    return cnt;
}

int Judge(int map[][9]){
    sum(map);
    int Main=cnt[2]-cnt[1],Other=calcu_matrix(map,2),Another;
    Another=0;
    //Another=Move_power(2);
    return Main*100+Other+Another;
}

int rec[10][9][9],Inform[9][2];
int Greed[25];

int Calcu_Next(int i,int j,int k,int Depth){
    int nx=i+mvx[move_list[k]],ny=j+mvy[move_list[k]];
    Deal_With(i,j,nx,ny,map[i][j],map);
    int ans=Judge(map);
    Copy(rec[Depth],map);
    return ans;
}

int MVL[10][25],TP[10]; 
bool can_move2(int x,int y,int Depth){
    TP[Depth]=0;
    int nx,ny;
    for(int i=1;i<=24;i++){
        nx=x+mvx[i],ny=y+mvy[i];
        if(nx>=1 && nx<=7 && ny>=1 && ny<=7 && map[nx][ny]==0)
            MVL[Depth][++TP[Depth]]=i;
    }
    return TP[Depth]!=0;
}

bool cmp1(const int &A,const int &B){
    return Greed[A]>Greed[B];
}
bool cmp2(const int &A,const int &B){
    return Greed[A]<Greed[B];
}

//假设电脑是得分者 
void Search1(int Depth){
    if(Depth>3){
        Inform[Depth-1][1]=Min(Inform[Depth-1][1],Judge(map));
        return ;
    }
    Copy(map,rec[Depth]);
    //如果是我(电脑)下 
    for(int i=1;i<=7;i++){
        for(int j=1;j<=7;j++)
            if(map[i][j]==2 && can_move2(i,j,Depth)){
                for(int k=1;k<=TP[Depth];k++)
                    Greed[k]=Calcu_Next(i,j,k,Depth);
                //把贪心中容易得分的先下 
                for(int k=1;k<=TP[Depth];k++)
                    for(int l=1;l<=TP[Depth]-k;l++)
                        if(Greed[l]<Greed[l+1]){
                            int tmp=Greed[l];Greed[l]=Greed[l+1];Greed[l+1]=tmp;
                            tmp=MVL[Depth][l];MVL[Depth][l]=MVL[Depth][l+1];MVL[Depth][l+1]=tmp;
                        }
                
                for(int k=1;k<=TP[Depth];k++){
                    int nx=i+mvx[MVL[Depth][k]],ny=j+mvy[MVL[Depth][k]],Interest;
                    Deal_With(i,j,nx,ny,2,map);
                    Inform[Depth+1][0]=-INF;
                    Inform[Depth+1][1]=INF;
                    
                    Search2(Depth+1);
                    Copy(rec[Depth],map);
                    if(Inform[Depth-1][1]<=Inform[Depth][0]) return;
                    
                }
            }
    }
    Inform[Depth-1][1]=Min(Inform[Depth-1][1],Inform[Depth][0]);
}

void Search2(int Depth){
    if(Depth>3){
        Inform[Depth-1][0]=Max(Inform[Depth-1][0],Judge(map));
        return ;
    }
    Copy(map,rec[Depth]);
    //如果是阻碍者下 
    for(int i=1;i<=7;i++){
        for(int j=1;j<=7;j++)
            if(map[i][j]==1 && can_move2(i,j,Depth)){
                for(int k=1;k<=TP[Depth];k++)
                    Greed[k]=Calcu_Next(i,j,k,Depth);
                //把贪心中难以得分的先下 
                for(int k=1;k<=TP[Depth];k++)
                    for(int l=1;l<=TP[Depth]-k;l++)
                        if(Greed[l]>Greed[l+1]){
                            int tmp=Greed[l];Greed[l]=Greed[l+1];Greed[l+1]=tmp;
                            tmp=MVL[Depth][l];MVL[Depth][l]=MVL[Depth][l+1];MVL[Depth][l+1]=tmp;
                        }
                
                for(int k=1;k<=TP[Depth];k++){
                    int nx=i+mvx[MVL[Depth][k]],ny=j+mvy[MVL[Depth][k]],Interest;
                    Deal_With(i,j,nx,ny,1,map);
                    Inform[Depth+1][0]=-INF;
                    Inform[Depth+1][1]=INF;
                    
                    Search1(Depth+1);
                    Copy(rec[Depth],map);
                    if(Inform[Depth-1][0]>=Inform[Depth][1]) return;
                }
            }
    }
    Inform[Depth-1][0]=Max(Inform[Depth-1][0],Inform[Depth][1]);
}

//这个就是搜索的过程了 
void COMPUTER3(){
    int MIN=-INF;
    int BEST_I,BEST_J,BEST_NI,BEST_NJ;
    Copy(map,rec[0]);
    Inform[0][0]=-INF;
    Inform[0][1]=INF;
    //如果是我(电脑)下 
    for(int i=1;i<=7;i++){
        for(int j=1;j<=7;j++)
            if(map[i][j]==2 && can_move(i,j)){
                for(int k=1;k<=top;k++)
                    Greed[k]=Calcu_Next(i,j,k,0);
                //把贪心中容易得分的先下 
                for(int k=1;k<=top;k++)
                    for(int l=1;l<=top-k;l++)
                        if(Greed[l]<Greed[l+1]){
                            int tmp=Greed[l];Greed[l]=Greed[l+1];Greed[l+1]=tmp;
                            tmp=move_list[l];move_list[l]=move_list[l+1];move_list[l+1]=tmp;
                        }
                
                for(int k=1;k<=top;k++){
                    int nx=i+mvx[move_list[k]],ny=j+mvy[move_list[k]],Interest;
                    Deal_With(i,j,nx,ny,2,map);
                    Inform[1][0]=-INF;
                    Inform[1][1]=INF;
                    
                    Search2(1);
                    Copy(rec[0],map);
                    if(Inform[0][0]>MIN){
                        BEST_NI=nx;BEST_NJ=ny;BEST_I=i;BEST_J=j;
                        MIN=Inform[0][0]; 
                    }
                }
            }
    }
    if(MIN==-INF){printf("不好意思它挂机了！");return;} 
    Deal_With(BEST_I,BEST_J,BEST_NI,BEST_NJ,2,map);
    printf("电脑把(%d,%d)移动到了(%d,%d):\n",BEST_I,BEST_J,BEST_NI,BEST_NJ);
}

//单人游戏操作 
void operation1(){
    int x1,y1,x2,y2;
    while(true){
        print2(map);
        if(!cnt[0]){
            if(cnt[1]>cnt[2]) printf("您赢了!Orz!");
            else printf("您差点就赢了!Orz!");
            return ;
        }
        int f1=false,f2=false;
        for(int i=1;i<=7;i++)
            for(int j=1;j<=7;j++)
                if(map[i][j]==1 && !f1){
                    if(can_move(i,j)) f1=true;
                }
        if(!f1) {printf("您差点就赢了!Orz!");return;}
        int ord; 
        printf("您需要存档吗？如果需要请输入1否则输入0\n");
        scanf("%d",&ord); 
        if(ord)    {printf("已存档！\n");Save1();return ;}
        bool Over=0;
        while(true){
            printf("请输入您需要移动的棋子的行和列\n");
            scanf("%d%d",&x1,&y1);
            if(map[x1][y1]!=1)
                printf("您在该位置没有棋子!\n");
            else if(!can_move(x1,y1)) printf("您选择的棋子无法移动!\n");
            else{
                while(true){
                    printf("请输入您需要移动的棋子到的位置：\n");
                    scanf("%d%d",&x2,&y2); 
                    if(abs(x2-x1)>2 || abs(y2-y1)>2 || (x1==x2 && y1==y2) || map[x2][y2]){
                        printf("您的移动不合法！\n"); break;
                    }
                    else{
                        Over=1;
                        break;
                    }
                }
            }
            if(Over) break;
        }
        Deal_With(x1,y1,x2,y2,1,map);
        print2(map); 
        for(int i=1;i<=7;i++)
            for(int j=1;j<=7;j++)
                if(map[i][j]==2 && !f2)
                    if(can_move(i,j)) f2=true;
        if(!f2) {printf("您赢了!Orz!");return;}
        if(!cnt[0]){
            if(cnt[1]>cnt[2]) printf("PLAYER1赢了!Orz!");
            else printf("PLAYER2赢了!Orz!");
            return ;
        }    
        COMPUTER3();
    }
}

//双人游戏操作 
void operation2(){
    int x1,y1,x2,y2;
    while(true){
        bool f1=false,f2=false;
        print2(map); 
        for(int i=1;i<=7;i++)
            for(int j=1;j<=7;j++)
                if(map[i][j]==1 && !f1)
                    if(can_move(i,j)) f1=true;
        if(!f1) {printf("PLAYER2赢了!Orz!");return;}
        if(!cnt[0]){
            if(cnt[1]>cnt[2]) printf("PLAYER1赢了!Orz!");
            else printf("PLAYER2赢了!Orz!");
            return ;
        }
        
        int ord;
        printf("您需要存档吗？如果需要请输入1否则输入0\n");
        scanf("%d",&ord); 
        if(ord)    {printf("已存档！\n");Save2();return ;}
        
        bool Over=0;
        while(true){
            printf("现在是PLAYER1操作！\n请输入您需要移动的棋子的行和列\n");
            scanf("%d%d",&x1,&y1);
            if(map[x1][y1]!=1)
                printf("您在该位置没有棋子!\n");
            else if(!can_move(x1,y1)) printf("您选择的棋子无法移动!\n");
            else{
                while(true){
                    printf("请输入您需要移动的棋子到的位置：\n");
                    scanf("%d%d",&x2,&y2); 
                    if(abs(x2-x1)>2 || abs(y2-y1)>2 || (x1==x2 && y1==y2) || map[x2][y2]){
                        printf("您的移动不合法！\n"); break;
                    }
                    else{
                        Over=1;
                        break;
                    }
                }
            }
            if(Over) break;
        }
        Deal_With(x1,y1,x2,y2,1,map);
        print2(map); 
        for(int i=1;i<=7;i++)
            for(int j=1;j<=7;j++)
                if(map[i][j]==2 && !f2)
                    if(can_move(i,j)) f2=true;
        if(!f2) {printf("PLAYER1赢了!Orz!");return;}
        if(!cnt[0]){
            if(cnt[1]>cnt[2]) printf("PLAYER1赢了!Orz!");
            else printf("PLAYER2赢了!Orz!");
            return ;
        }
        
        Over=0;
        while(true){
            printf("现在是PLAYER2操作！\n请输入您需要移动的棋子的行和列\n");
            scanf("%d%d",&x1,&y1);
            if(map[x1][y1]!=2)
                printf("您在该位置没有棋子!\n");
            else if(!can_move(x1,y1)) printf("您选择的棋子无法移动!\n");
            else{
                while(true){
                    printf("请输入您需要移动的棋子到的位置：\n");
                    scanf("%d%d",&x2,&y2); 
                    if(abs(x2-x1)>2 || abs(y2-y1)>2 || (x1==x2 && y1==y2) || map[x2][y2]){
                        printf("您的移动不合法！\n"); break;
                    }
                    else{
                        Over=1;
                        break;
                    }
                }
            }
            if(Over) break;
        }
        Deal_With(x1,y1,x2,y2,2,map);

    }
}

 

　　【未完待续...持续更新】

　　笔者最近在忙线代的自习和作业，可能暂时没有时间更新呀...对不起啦~不过闲下来还会思考的...