BZOJ 4011 HNOI2015 落忆枫音

AC通道：http://www.lydsy.com/JudgeOnline/problem.php?id=4011

 

题目很长，写得也很有诗意与浪漫色彩，让我们不禁感叹出题人是一个多么英俊潇洒的人。

 

所以题目大意就是：

　　给一个有向无环图，问加上一条我给定的边后，有多少个以1为根的树形图？n<=1e5,m<=2*1e5

原图无重边，加上的边可以为自环。

　　

首先先来解决一个问题：

　　一个有向无环图的树形图有多少个呢？ 

相当于除了根节点以外，每个点随意取一个入度，为什么就一棵树呢？每个点选一个父亲，并且保证没有环，所以是一棵树。

好的，对于有向无环图就一定是这样的，那么若加入一条边<x,y>，

那么就可能再选择的过程中选出一个环[就是祖先的父亲是自己这种情况]。那么我们就需要删去这种情况。

首先要出现环，则必定包括了<x,y>这条边，剩下的部分是原图中y->x的一条路径，要求这条路径上的点必须选择一条路径使得构成一个环。而其它的点可以随意选。

设F(i)表示y->i上的点所成路径必须选择一条能构成环路径的方案数。

有初始值：

      

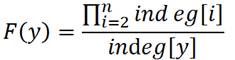
递推式：

　　 

相当于j可以选择延续所有从y走来的i的路径，但是要除以j原本可以选择的路径总数。

最后答案=所有方案[入度乘积] - F(x)。

 

听说ZZD去年就想出来了这题，不过因为不会打逆元而失之交臂[不然就是省队了？%%%]

为什么会有逆元？...额我好像忘记说方案数要取模了...

那么这题中为了加速运算，就用了一个O(n)递推求1...n的所有逆元的方法，我也算是普及一下吧？...

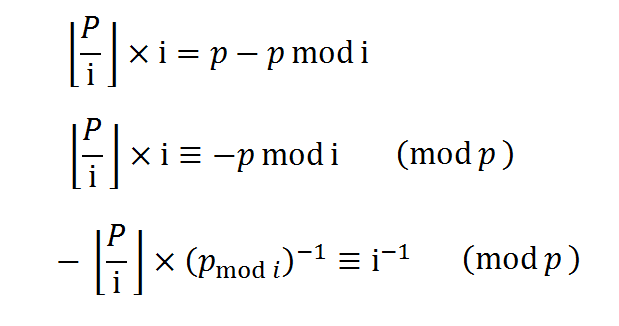
画图的时候没太注意大小写，不要太在意...

那么i的逆元可以由p mod i的逆元得知了，这显然是一个已知的数，所以每次递推都是O(1)的，边界：1的逆元=1。

 

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

inline int in(){
    int x=0;char ch=getchar();
    while(ch>'9' || ch<'0') ch=getchar();
    while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
    return x;
}

const int maxn=100010;
const int mod=1e9+7;
typedef long long ll;

struct Node{
    int data,next;
}node[maxn<<1];

#define now node[point].data
#define then node[point].next

int n,m,ans,cnt,x,y;
int head[maxn],d[maxn],ld[maxn];
int f[maxn],stack[maxn],top;
int inv[maxn<<1];

void init(){
    inv[1]=1;
    for(int i=2;i<=m;i++)
        inv[i]=(mod-(ll)inv[mod%i]*(mod/i)%mod)%mod;
}

void add(int u,int v){
    node[cnt].data=v;node[cnt].next=head[u];head[u]=cnt++;d[v]++;
}

int power(int a,int k){
    int ans=1;
    for(;k;k>>=1){
        if(k&1) ans=(ll)ans*a%mod;
        a=(ll)a*a%mod;
    }
    return ans;
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("maple.in","r",stdin);
    freopen("maple.out","w",stdout);
#endif

    int u,v;

    n=in(),m=in();
    x=in(),y=in();
    init();
    for(int i=1;i<=n;i++) head[i]=-1;
    for(int i=1;i<=m;i++)
        u=in(),v=in(),add(u,v);
    d[y]++;
    ans=1;
    for(int i=2;i<=n;i++) ans=(ll)ans*d[i]%mod; 
    if(y==1){ printf("%d",ans);return 0;}
    else f[y]=(ll)ans*inv[d[y]]%mod;
    
    d[y]--;
    memcpy(ld,d,sizeof(d));
    for(int i=1;i<=n;i++) if(!d[i]) stack[++top]=i;
    
    while(top){
        u=stack[top--];
        for(int point=head[u];point!=-1;point=then){
            if(--d[now]==0)
                stack[++top]=now;
            f[now]=(f[now]+(ll)f[u]*inv[ld[now]]%mod)%mod;
        }
    }
    
    ans=(ans-f[x]+mod)%mod;
    printf("%d",ans);
    return 0;
}