BZOJ3130 [Sdoi2013]费用流

AC通道：http://www.lydsy.com/JudgeOnline/problem.php?id=3130

这题codevs上也有，不过数据挂了[要A得看discuss]。

 

题目大意：

Alice来弄一条最大流，Bob来给Alice弄好的最大流定权值。

定权值的方法是给没条边定一个值wi，然后wi*flow(i)的和就是总的费用，但要求所有wi之和为p。

现在Bob希望最后的费用最大，即对于每一种最大流方案都会有一种最大的定值方案。

Alice则希望花费最小，即选出一种最大流方案，使得这种方案的最大定值是所有最大流方案中最小的。

求最大流，及这个最小的最大定值。

 

首先我们先从Bob的角度出发。

怎么给一种最大流方案定值就能最大呢？

显然是给最大流中流量最大的边订上p的值就可以了。

因为最后也是加法，然后满足分配率，然后随便证一下，感受一下就是对的了。

 

然后从Alice的角度来想，恩不就是让流量最大的边最小么？...

然后就限制流量跑最大流啊，如果和原来相同就可以了。

这个流量限制就是典型的二分咯...不过注意往常的网络流都是跑整数流量，但是这题不是，我们要实数二分最大流量

因为往常边都是整数的边，最大流跑整数的一定可以跑出来，不过现在毕竟限流的情况，那么我们要跑小数咯...

如果你还不信，给你一个样例好了[来自ZYF-ZYF]：

 

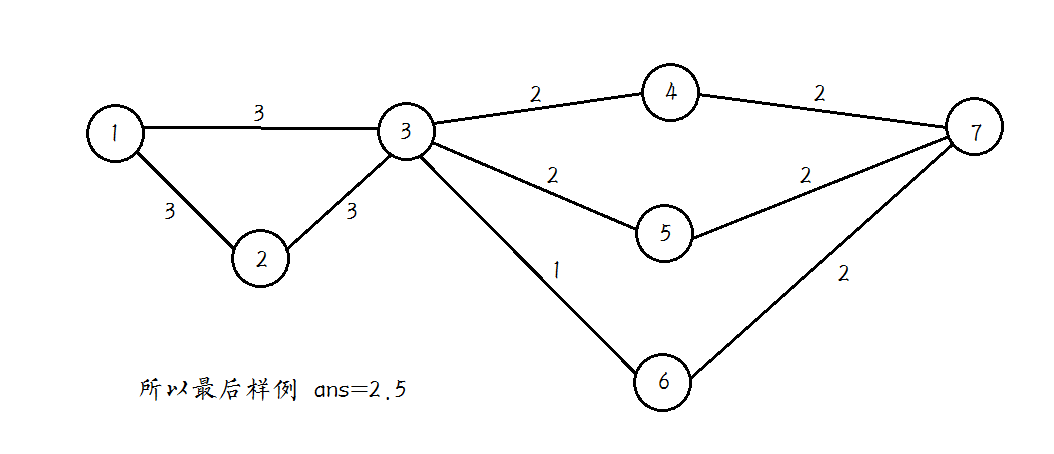
所以呢= =大家注意精度控制好了...不懂看看代码也行。

 

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>

using namespace std;

const int maxn=110;
const int maxm=1010;
const int INF=0x3f3f3f3f;
const double eps=1e-6;

struct Node{
    int data,next;
    double low;
}node[maxm<<1];

#define now node[point].data
#define www node[point].low
#define then node[point].next

struct Edge{
    int u,v;
    double w;
}edge[maxm];

int n,m,p,cnt;
int s,t;
double ans;
int dis[maxn],que[maxn];
int head[maxn],cur[maxn];

void add(int u,int v,double w){
    node[cnt].data=v;node[cnt].next=head[u];node[cnt].low=w;head[u]=cnt++;
    node[cnt].data=u;node[cnt].next=head[v];node[cnt].low=0;head[v]=cnt++;
}

bool BFS(){
    memset(dis,-1,sizeof(dis));
    int H=0,T=1;que[1]=1;dis[1]=0;
    while(H<T){
        H++;
        for(int point=head[que[H]];point!=-1;point=then)
            if(www>eps && dis[now]<0){
                dis[now]=dis[que[H]]+1;
                que[++T]=now;
            }
    }
    return dis[t]>0;
}

double dfs(int x,double low){
    if(x==t) return low;
    double Low;
    for(int &point=cur[x];point!=-1;point=then)
        if(www>eps && dis[now]==dis[x]+1){
            Low=dfs(now,min(low,www));
            if(Low>eps){
                www-=Low,node[point^1].low+=Low;
                return Low;
            }
        }
    return 0;
}

double check(double mid){
    cnt=0;
    for(int i=1;i<=n;i++) head[i]=-1;
    for(int i=1;i<=m;i++)
        add(edge[i].u,edge[i].v,min(edge[i].w,mid));
    
    double flag,sum=0;
    while(BFS()){
        memcpy(cur,head,sizeof(head));
        while((flag=dfs(s,INF))>eps)
            sum+=flag;
    }
    return sum;
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("3130.in","r",stdin);
    freopen("3130.out","w",stdout);
#endif
    int u,v,w;
    double l=0,r=0,mid;

    scanf("%d%d%d",&n,&m,&p);
    s=1,t=n;
    for(int i=1;i<=n;i++) head[i]=-1;
    for(int i=1;i<=m;i++)
        scanf("%d%d%lf",&edge[i].u,&edge[i].v,&edge[i].w),r=max(r,edge[i].w);
    
    ans=check(r);
    while(r-l>eps){
        mid=(l+r)/2;
        if(fabs(ans-check(mid))<eps) r=mid;
        else l=mid;
    }
    
    printf("%.0lf\n%.5lf",ans,l*p);
    
    return 0;
}