Codeforces Round #343 (Div. 2)
1.前言:感觉很久没有全机房形式的做过一次CF了...居然星期六他们打了一场4人局?...Orz我校神犇OICyan成功AK。最近正需要调整一下状态,于是就跟着刷了这次的CF,感觉智商被碾压,想题速度和打题速度果然很捉鸡...所以打一场还是有些收获吧。
2.Problem A
题目大意:给你一个n*n的棋盘,某些棋盘上放了棋子,问:在同行或同列的棋子有多少对。(n<=100)
水题。假设某行有x个,那么就有C(x,2)对。然后每行每列统计有多少个就行了,复杂度O(n^2)。

#include<cstdio> #include<cstring> using namespace std; int n,ans; int cnt_H[110],cnt_L[110]; char ch[110][110]; int main(){ // freopen("A.in","r",stdin); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%s",ch[i]+1); for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++) if(ch[i][j]=='C') cnt_H[i]++; for(int j=1;j<=n;j++) if(ch[j][i]=='C') cnt_L[i]++; } for(int i=1;i<=n;i++){ ans+=(cnt_H[i]*(cnt_H[i]-1))>>1; ans+=(cnt_L[i]*(cnt_L[i]-1))>>1; } printf("%d",ans); return 0; }
3.Problem B
题目大意:有n个人,其中有男人也有女人,第i个人出现的时间是[li,ri],设ans(time)表示在time时间时,min(出现的男人数,出现的女人数)*2,求time∈[1,366]中最大的ans(time)。(n<=5000)
因为时间段很短,可以考虑枚举每个时段有多少男人有多少女人。这就可以将人打散成两个端点(li和ri)并按时间排序,然后按时间一遍扫过去,然后求每个时刻的ans,从而得到全局的最大值。复杂度O(nlogn+n)。
这题输入部分一个','打成';'检查我好久...[果然检查题目不仔细...],以后还是不偷懒打'{}'吧...

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=5010; struct Node{ int x,pos; }s[maxn<<1]; int n,ans; bool cmp(const Node &A,const Node &B){ if(A.x!=B.x) return A.x<B.x; else return A.pos>B.pos; } int main(){ int l,r,rec=0; char sex[2]; scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%s",sex); scanf("%d%d",&l,&r); if(sex[0]=='F') s[++rec].x=l,s[rec].pos=1, s[++rec].x=r,s[rec].pos=-1; else s[++rec].x=l,s[rec].pos=2, s[++rec].x=r,s[rec].pos=-2; } sort(s+1,s+rec+1,cmp); int p=1,cnt[3]={0}; for(int i=1;i<=366;i++){ while(s[p].x==i){ if(s[p].pos<0){ ans=max(ans,min(cnt[1],cnt[2])); cnt[-s[p].pos]--; } else cnt[s[p].pos]++; p++; } ans=max(ans,min(cnt[1],cnt[2])); } printf("%d",ans<<1); return 0; }
4.Problem C
题目大意:给你一个长度为m的括号序列,问如果通过在它的前面和后面共补上n-m个括号,从而让它变成长度为n的,并且要合法的括号序列有多少种添加的方法。(n<=1e5,n-m<=2000)
这题想了比较久吧,感觉题目换一种方式说就是固定一段操作的出栈入栈序列的个数。当时想象画面,将序列又投射到平面上的起伏中。相当于在一段曲折的线段前后补一段折线段,使得整个折线段没有部分在x轴下,并且要能从(0,0)到(n,0)。
于是就变成枚举中间折线段的起点,然后对于一个起点(i,j)的贡献就是(0,0)到(i,j)的方案*(i+m,j+cnt)到(n,0)的方案数。当然要求中间的部分也不能到x下方,所以要求j>=min。[说的比较抽象,看图吧]
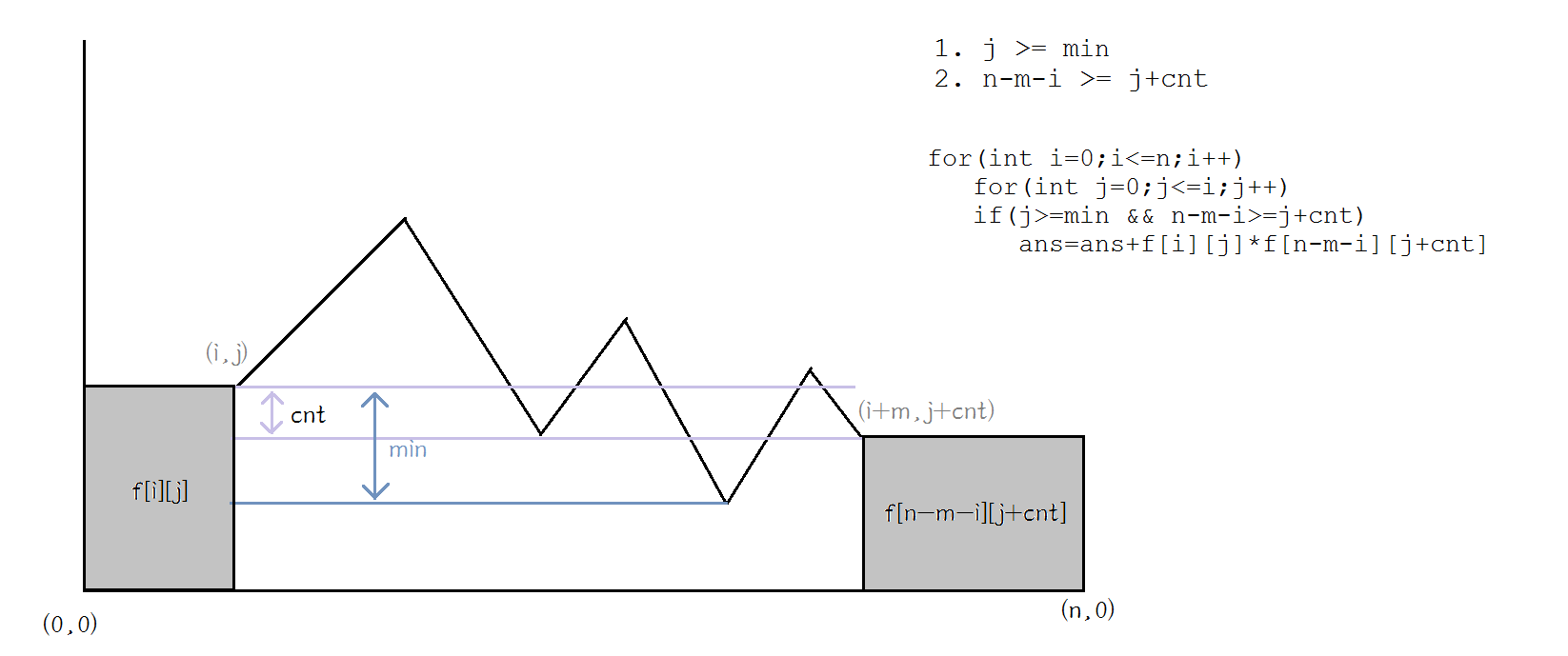
图中貌似枚举部分i<=n-m在上图中打错了,不过只是小细节吧...大致的思路还是来源于以前catalan数的坐标表示,其中的f[][]也是由坐标表示的递推方程递推而来。

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=100010; const int maxL=2010; const int mod=1e9+7; typedef long long ll; int n,m,L,ans; int f[maxL][maxL]; char s[maxn]; int main(){ int cnt=0,Lim=0; scanf("%d%d",&n,&m);L=n-m; scanf("%s",s); for(int i=0;i<m;i++){ if(s[i]=='(') cnt++; else cnt--; Lim=min(Lim,cnt); } f[0][0]=1; for(int i=1;i<=L;i++){ f[i][0]=f[i-1][1]; for(int j=1;j<=L;j++) f[i][j]=(f[i-1][j-1]+f[i-1][j+1])%mod; } for(int i=0;i<=L;i++) for(int j=0;j<=i;j++) if(j+Lim>=0 && j+cnt<=n-m-i) ans=(ans+(ll)f[i][j]*f[n-m-i][j+cnt]%mod)%mod; printf("%d",ans); return 0; }
5.Problem D
题目大意:给你n个蛋糕,只有若i想放在j上,必须i<j且i的体积最小,求一种放置方案使得最终堆积的蛋糕体积最大,输出最大体积。(n<=100000)
我的思路是给体积[离散化]建线段树,按时间将蛋糕一个一个加入,每次查询体积比它小的能通过堆积达到的最大值,然后用Max+当前体积作为新的值记录在这个位置更新线段树,并用这个值随时更新答案。这题long long需要小心!

#include<cmath> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=100010; const double pi=acos(-1); typedef long long ll; inline int in(){ int x=0;char ch=getchar(); while(ch>'9' || ch<'0') ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar(); return x; } int n,cnt; ll ans; ll f[maxn<<2],Fmax[maxn<<2]; ll rv[maxn],v[maxn],Hash[maxn]; int get_rk(ll x){ int l=0,r=cnt+1,mid; while(l<r-1){ mid=(l+r)>>1; if(Hash[mid]>x) r=mid; else l=mid; } return l; } void modify(int node,int l,int r,int x,ll d){ if(l==r){f[node]=Fmax[node]=d;return;} int mid=(l+r)>>1; if(x>mid) modify(node<<1|1,mid+1,r,x,d); else modify(node<<1,l,mid,x,d); Fmax[node]=max(Fmax[node<<1],Fmax[node<<1|1]); } ll get_max(int node,int l,int r,int al,int ar){ if(al>ar) return 0; if(al==l && ar==r) return Fmax[node]; int mid=(l+r)>>1; if(ar<=mid) return get_max(node<<1,l,mid,al,ar); else if(al>mid) return get_max(node<<1|1,mid+1,r,al,ar); else return max(get_max(node<<1,l,mid,al,mid),get_max(node<<1|1,mid+1,r,mid+1,ar)); } int main(){ //freopen("D.in","r",stdin); int r,h; n=in(); for(int i=1;i<=n;i++){ r=in(),h=in(); v[i]=(ll)r*r*h; } memcpy(rv,v,sizeof(rv)); sort(v+1,v+n+1); Hash[++cnt]=v[1]; for(int i=2;i<=n;i++){ while(v[i]==v[i-1] && i<n) i++; Hash[++cnt]=v[i]; } int key; ll Max; key=get_rk(rv[1]); ans=max(ans,rv[1]); modify(1,1,n,key,rv[1]); for(int i=2;i<=n;i++){ key=get_rk(rv[i]); Max=get_max(1,1,n,1,key-1); ans=max(ans,Max+rv[i]); modify(1,1,n,key,Max+rv[i]); } printf("%lf",(double)ans*pi); return 0; }
6.Problem E
题目大意:给你一棵树,然后每次询问两个点,求随机添上一条边后,两点所在的简单环的长度的期望值[如果加的边不能使它们俩处于同一个环这条边就不会计入期望值的贡献]。(n,q<=100000)
首先分析一下样例,然后就开始画图咯,因为有根树比较好做,就画一颗有根树,发现连边的情况大致有两种:
一是Lca(u,v)!=v,即u不在v的子树下,那么任意连接u子树中的某个点与v子树中某个点就可以让u,v同环了。然后怎么算环的期望呢,就可以先考虑固定u子树中的某个点ui,那么就是
dis(u,i)*size(v)+v子树中每个点到v的距离和+(d[v]+d[u]-d[Lca]*2+1)*size(v)
然后定义ddc(x)[down_dis_commit]为x的子树中所有节点到x的距离和,刚刚的ui贡献值为:
dis(u,i)*size(v)+ddc(v)+(d[v]+d[u]-d[Lca]*2+1)*size(v)
将u的子树中所有点的贡献相加,那么就是:
ddc(u)*size(v)+ddc(v)*size(u)+(d[v]+d[u]-d[Lca]*2)*size(v)*size(u)
然后其中共size(u)*size(v)条路径,将总贡献/路径数就是最后的期望了。
第二种情况就是Lca(u,v)=v的情况,那么现在就需要抽象一下,把v节点折下来,就变成上面的问题了。

其中两个需要统计的信息都可以分别通过一遍dfs得到,其中的枢纽是ddc(root)=adc(root)。然后后面的询问就好办了,看代码的两个问题划归部分,感觉写的挺舒服...
注意这题的距离和也是会爆int的,又被坑了....

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; inline int in(){ int x=0;char ch=getchar(); while(ch>'9' || ch<'0') ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar(); return x; } const int maxn=100010; typedef long long ll; struct Node{ int data,next; }node[maxn<<1]; #define now node[point].data #define then node[point].next int n,m,cnt; int head[maxn],d[maxn]; int sz[maxn]; ll Ddc[maxn],Adc[maxn];//Down_dis_commit,All_dis_commit int f[maxn][18]; double ans; void add(int u,int v){ node[cnt].data=v;node[cnt].next=head[u];head[u]=cnt++; node[cnt].data=u;node[cnt].next=head[v];head[v]=cnt++; } void dfs(int x,int fa){ for(int i=1;i<=17;i++) f[x][i]=f[f[x][i-1]][i-1]; for(int point=head[x];point!=-1;point=then) if(now!=fa){ f[now][0]=x;d[now]=d[x]+1; dfs(now,x); sz[x]+=sz[now]; Ddc[x]+=Ddc[now]+sz[now]; } sz[x]++; } void dfs2(int x,int fa){ if(fa) Adc[x]=Adc[fa]+n-(sz[x]<<1); for(int point=head[x];point!=-1;point=then) if(now!=fa) dfs2(now,x); } int LCA(int x,int y){ int tmp=d[x]-d[y]; for(int i=17;i>=0;i--) if((1<<i)&tmp) x=f[x][i]; if(x==y) return x; for(int i=17;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } int get_fa(int x,int t){ for(int i=17;i>=0;i--) if((1<<i)&t) x=f[x][i]; return x; } int main(){ // freopen("E.in","r",stdin); int u,v,x,L,Lca; n=in();m=in(); for(int i=1;i<=n;i++) head[i]=-1; for(int i=1;i<n;i++) u=in(),v=in(),add(u,v); dfs(1,0); Adc[1]=Ddc[1]; dfs2(1,0); while(m--){ u=in(),v=in(); if(d[u]<d[v]) swap(u,v); Lca=LCA(u,v); if(Lca==v){ x=get_fa(u,d[u]-d[v]-1); ll Ddcv=Adc[x]-Ddc[x]-n+sz[x],szv=n-sz[x]; ll rec=(ll)sz[u]*Ddcv+(ll)szv*Ddc[u]; ll tot=(ll)sz[u]*szv; ans=(double)rec/tot+d[u]-d[v]+1; } else{ ll rec=(ll)sz[u]*Ddc[v]+(ll)sz[v]*Ddc[u]; ll tot=(ll)sz[u]*sz[v]; ans=(double)rec/tot+d[u]+d[v]-d[Lca]*2+1; } printf("%.7lf\n",ans); } return 0; }
怎么说呢,考一场div2,虚拟比赛的时候打了1h20min就想弃疗了...不过这样考一场下来,觉得虽然都在能思考出的范围内,可是考场思考的不全面或是不能迅速想到一些接近正解的模型导致考试时不能切,考后才能做出来是值得反思的。正如lyy所说的,刷CF确实能让人的思维更具有弹性吧...以后有机会还要继续。思考的乐趣就孕育其中...




