BZOJ 2301 Problem b
AC通道:http://www.lydsy.com/JudgeOnline/problem.php?id=2301
冬令营听了莫比乌斯,这就是宋老师上课讲的例题咯[今天来实现一下]

1 #include<cstdio>
2 #include<cstring>
3 #include<algorithm>
4
5 using namespace std;
6
7 inline int in(){
8 int x=0;char ch=getchar();
9 while(ch>'9' || ch<'0') ch=getchar();
10 while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
11 return x;
12 }
13
14 const int maxn=50010;
15
16 int mu[maxn],s[maxn];
17 int Prime[maxn],cnt;
18 bool no_prime[maxn];
19
20 void get_prime(){
21 int tmp;mu[1]=1;
22 for(int i=2;i<maxn;i++){
23 if(!no_prime[i]) Prime[++cnt]=i,mu[i]=-1;
24 for(int j=1;j<=cnt && ((tmp=Prime[j]*i)<maxn);j++){
25 no_prime[tmp]=true;
26 if(i%Prime[j]==0){mu[tmp]=0;break;}
27 mu[tmp]=-mu[i];
28 }
29 }
30 for(int i=1;i<maxn;i++) s[i]=s[i-1]+mu[i];
31 }
32
33 //j表示在所有数x中n/x=n/i的最后一个
34 long long calcu(int n,int m){
35 long long sum=0;
36 if(n>m) swap(n,m);
37 for(int i=1,j=0;i<=n;i=j+1){
38 j=min(n/(n/i),m/(m/i));
39 sum+=(long long)(s[j]-s[i-1])*(m/i)*(n/i);
40 }
41 return sum;
42 }
43
44 int main(){
45 #ifndef ONLINE_JUDGE
46 freopen("2301.in","r",stdin);
47 freopen("2301.out","w",stdout);
48 #endif
49
50 int T,a,b,c,d,k;
51 long long ans;
52
53 get_prime();
54 T=in();
55 while(T--){
56 a=in(),b=in(),c=in(),d=in(),k=in();
57 ans=calcu(b/k,d/k)-calcu(b/k,(c-1)/k)-calcu((a-1)/k,d/k)+calcu((a-1)/k,(c-1)/k);
58 printf("%lld\n",ans);
59 }
60
61 return 0;
62 }
[感觉还是说一下怎么做吧...]不过建议大家还是找个ppt来看好啦[我没有图啊...]
首先将问题变成询问[i=1...n][j=1...m]中有多少gcd(i,j)==k的数
然后其实就是[i=1...n/k][j=1...m/k]中gcd(i,j)==1的数
然后设f(n,m,k)表示[i=1...n/k][j=1...m/k]中gcd(i,j)==1的个数
g(n,m,k)表示[i=1...n/k][j=1...m/k]中gcd(i,j)是1的倍数的个数 <- 小学生都知道这个等于(n/k)*(m/k)是吧
所以 这一步直接由定义推来
这一步直接由定义推来
然后莫比乌斯反演一下

然后再把g(n,m,k)的公式带一下
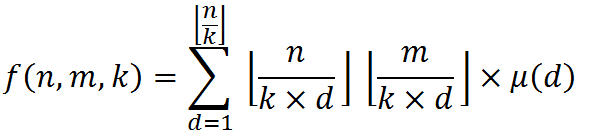
就是这个样子了...
然后发现有一大部分的数值是相同的,然后就可以看代码的分块了...




