Poj2420 A Star not a Tree? 模拟退火算法
题目链接:http://poj.org/problem?id=2420
题目大意:每组数据中给n个点(n<=100),求平面中一个点使得这个点到n个点的距离之和最小。
分析:一开始看到这个题想必是不好做的...因为平面太大了,不能使用枚举的方法,于是想到随机点出来比较。可是总不能无限的枚举,而且随机点出的答案需要是最优值还是一个玄学问题。所以想到了模拟退火的方法。
具体操作:首先随意找一个点作为出发点,然后设置一个初始温度,使得这个点可以在这个温度下乱跑[但是只让它往上下左右跑]温度越高,这个点就越活跃,在所找到的区域中选一个到其他点距离和最小的点,然后跳过去。完成这一步后,温度降低,再在新的点附近搜。联想到刚开始学模拟退火时看到的一张图:
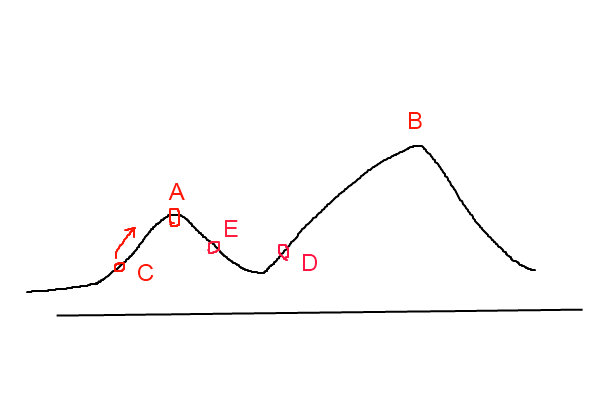
再配上一句经典的话:
爬山算法:兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法,它不能保证局部最优值就是全局最优值。
模拟退火:兔子喝醉了。它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高方向跳去。这就是模拟退火。
可以把我们的题目想像到这个图中去:
山峰类似距离和的函数,求最小值相当于找最高峰,一开始允许随便找,就可以跨过第一座看上去是最高的峰顶而去往其他的位置。当时当温度降下来[或是酒慢慢醒了]就只能在比较近的位置找了,直到某个位置跳上了最高峰,得到最后的答案。
但是毕竟这个起始温度和降低温度的速度还是有些玄学的。所以不妨开得大一点保险好了...
AC代码

1 #include<cstdio> 2 #include<cmath> 3 4 using namespace std; 5 6 const int maxn=110; 7 const int T=100000; 8 const int INF=0x7fffffff; 9 const double eps=1e-8; 10 const double delta=0.98; 11 12 struct Node{double x,y;}node[maxn]; 13 14 int n; 15 int dx[4]={0,0,1,-1}; 16 int dy[4]={1,-1,0,0}; 17 18 inline double dis(Node A,Node B){ 19 return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y)); 20 } 21 22 double sum_dis(Node A){ 23 double sum=0; 24 for(int i=1;i<=n;i++) 25 sum+=dis(A,node[i]); 26 return sum; 27 } 28 29 void search(){ 30 Node Ans=node[1],Now; 31 double t=T,res=INF; 32 bool find; 33 while(t>eps){ 34 find=true; 35 while(find){ 36 find=false; 37 for(int j=0;j<4;j++){ 38 Now.x=Ans.x+dx[j]*t; 39 Now.y=Ans.y+dy[j]*t; 40 double Dis=sum_dis(Now); 41 if(Dis<res) 42 res=Dis,Ans=Now,find=true; 43 } 44 } 45 t=t*delta; 46 } 47 if(res-(int)(res)>0.5) 48 printf("%d\n", (int)(res+1)); 49 else 50 printf("%d\n", (int)(res)); 51 } 52 53 int main(){ 54 #ifndef ONLINE_JUDGE 55 freopen("Poj2420.in","r",stdin); 56 freopen("Poj2420.out","w",stdout); 57 #endif 58 59 while(~scanf("%d",&n)){ 60 for(int i=1;i<=n;i++) 61 scanf("%lf%lf",&node[i].x,&node[i].y); 62 search(); 63 } 64 65 return 0; 66 }




