卡特兰数（Catalan）与斯特林数（Stirling）

Part One 卡特兰数（Catalan）

一、组合含义

1.从 (0, 0) 走到 (𝑛, 𝑛)，且不越过 𝑦 = 𝑥 的方案数

2.凸多边形三角剖分问题

3.二叉树计数

4.长度为 2𝑛 的匹配括号序列的个数

……

二、Catalan数的求值

1.递归式

$\forall n\in \mathbb{N}\\ c(n)= \begin{cases} 1& \text{ if } n\in \left [ 0,1 \right ] \\ \sum_{i=0}^{n-1}c\left ( i \right ) c(n-1-i)& \text{ if } n\in \left [ 2,+\infty \right ] \end{cases}$

通常用于对Catalan数的辨识或用于较小数据求解
　　1,1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796

1 c[0]=1,c[1]=1;
2 for(int i=2;i<=n;i++)              
3     for(int j=0;j<i;j++) 
4         c[i]+=c[j]*c[i-j-1];

2.方格问题

$C_{n}=\begin{pmatrix} 2n\\ n \end{pmatrix}-\begin{pmatrix} 2n\\ n-1 \end{pmatrix}$

组合数递推式

1 for(int i=1;i<=2*n;i++){
2     c[i][0]=c[i][i]=1;
3     for(int j=1;j<i;j++)
4         c[i][j]=c[i-1][j]+c[i-1][j-1];
5     }
6 printf("%lld",c[2*n][n]-c[2*n][n-1]);

扩展

$\binom{2n}{n-m}-\binom{2n}{n-m-1}$

$C_{n}=\frac{1}{n+1}\begin{pmatrix} 2n\\ n \end{pmatrix}$

大数据取模需使用逆元

1 //上一种将最后一句改为
2 printf("%lld",c[2*n][n]/(n+1));

3.递推式

$C(n)=C(n-1)*(4*n-2)/(n+1)$

大数据谨慎使用

递推

1 c[0]=c[1]=1;
2 for(int i=2;i<=n;i++)
3     c[i]+=c[i-1]*(4*i-2)/(i+1);

递归

1 int c(int n){
2     if(n==0||n==1) return 1;
3     return c(n-1)*(4*n-2)/(n+1);
4 }

4.括号匹配问题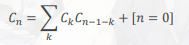

5.生成函数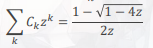

三、Catalan数的应用与习题

1.格路径问题

类似地，我们可以将Catalan数的定义扩展到n*m的网格中

$C_{n}= \binom{n+m}{m}-\binom{n+m}{m+1}$

2.赌徒问题

假设有一个赌徒初始时有1元，每次赌博以 1 − 𝑝 的概率获得一元，以 𝑝 的概率赔一元，那么赌徒输光钱的概率是多少？

3.高维几何体

𝑛 维超立方体的上共有多少个 𝑚 维超立方体呢？

$\binom{n}{m}2^{n-m}$

解释：n维中可任取m维，剩余（n-m）维存在取和不取两种情况

4.洛谷习题（之后会补上代码）

P1044 栈（纯裸题）

P3200 [HNOI2009]有趣的数列

P1375 小猫

P2532 [AHOI2012]树屋阶梯

P1722 矩阵 II

P1976 鸡蛋饼

P3978 [TJOI2015]概率论

Part Two 斯特林数（Stirling）

一、代数含义

$\begin{Bmatrix} x^{n} \end{Bmatrix}$ 和 $\begin{Bmatrix} x^{ \underline{n}} \end{Bmatrix}$ 两个序列互相表示的问题

二、第二类斯特林数

1. $x^n=\sum_{k}\begin{Bmatrix} n\\ k \end{Bmatrix}x^{ \underline{k}}$ 其中转移系数 $\begin{Bmatrix} n\\ k \end{Bmatrix}=\frac{\left ( \Delta ^{k}x^n\right )_{0} }{k!}$ 为第二类斯特林数