ARC127F ±AB

题目链接

首先，若 \(A + B \le M +1\)，根据 periodicity lemma 可以得到每个点均可达。

排除这种情况后，考虑：

• 若 \(V \ge B\)，令 \(V \gets V - B\)
• 否则若 \(V +A \le M\)，令 \(V \gets V+A\)
• 否则停止

设 \(V < A + B\)，且忽略 \(M\) 的限制，则 \(V\) 可以不重复地遍历 \([0, A + B)\) 中的所有数（只需要注意到 \([A, A + B)\) 中的所有数都会被遍历一次，随后不断减 \(B\)）

但是有 \(A + B > M + 1\)，因此这个环中至少有一个数不可达。

现在从起点开始向环上两个方向走（即对 \((A, B)\), \((B, A)\) 分别重复以上过程，将经过的数个数相加即可。

下面证明所有可达的点都可以在这个环上达到：

在一步可达的点之间连一条边，则在上述条件下每个点的度数至多为 \(2\)。

通过分类讨论得知（\(V - A \ge 0\) 或 \(V + B \le M\)，两者不同时成立），如果我们构造的环没有包括原图上的边会产生矛盾。

---

现在需要计数上面的操作次数。

重新描述问题，求出最小的 \(k\)，满足

\[\begin{aligned} &(V + kA) \bmod B > M - A\\ \iff& M - A + 1 - (V \bmod B)\ \boldsymbol\le\ kA \bmod B\ \boldsymbol\le\ B - 1 - (V \bmod B) \end{aligned} \]

（\(V \bmod B + A > M\) 的情况答案可以直接算出）

可以将问题再次描述为：高 \(A\) 长 \(B\) 的矩形上，从 \((0, 0)\) 出发向 \(y = x\) 方向走，如果超出某个边界就移动到对侧，第一次经过 \(y = 0, x \in [l, r]\) 的 \(x\)。之后只需用 exgcd 就可以解出 \(k\)。

这个问题直接递归就可以解决。（注意 \([l, r]\) 可能是一段前缀和一段后缀组成的区间）

下面是这个过程的示意图（来自 atcoder）

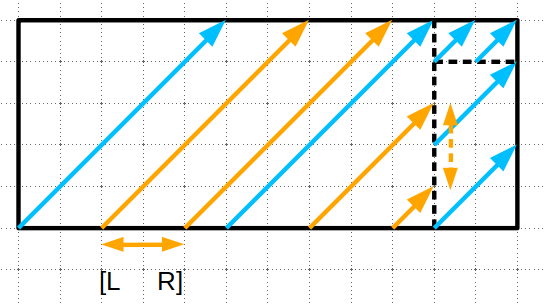
复杂度为对数级别。

#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#include <numeric>
#include <cassert>
using namespace std;

#define LOG(f...) fprintf(stderr, f)
#define DBG(f...) printf("%3d: ", __LINE__), printf(f)
// #define DBG(f...) void()
#define all(cont) begin(cont), end(cont)
#ifdef __linux__
#define getchar getchar_unlocked
#define putchar putchar_unlocked
#endif

using ll = long long;

template <class T> void read(T &x) {
  char ch; x = 0;
  int f = 1;
  while (isspace(ch = getchar()));
  if (ch == '-') ch = getchar(), f = -1;
  do x = x * 10 + (ch - '0'); while(isdigit(ch = getchar()));
  x *= f;
}
template <class T, class ...A> void read(T &x, A&... args) { read(x); read(args...); }

pair<int, int> exgcd(int a, int b) {
  if (!b) return {1, 0};
  auto [x, y] = exgcd(b, a % b);
  return {y, x - a / b * y};
}
int inv(int x, int M) {
  int t = exgcd(x, M).first;
  return t < 0 ? t + M : t;
}

int recur(int h, int w, int l, int r) {
  int pos = (l + h - 1) / h * h % w;
  if ((l <= pos && pos <= r) || (l > r && (pos <= r || pos >= l)))
    return pos >= l ? pos - l : pos - l + w;
  if (h >= w) return recur(h % w, w, l, r);
  return (r - l) - recur(w % h, h, (h - r % h) % h, (h - l % h) % h);
}

int solve(int a, int b, int m, int v) {
  int vmb = v % b;
  if (vmb > m - a) return v / b;
  int r = recur(a, b, m + 1 - a - vmb, b - 1 - vmb) + (m + 1 - a - vmb);
  int k = (ll)r * inv(a, b) % b;
  return k + (((ll)k * a + v) / b);
}

int main() {
#ifndef ONLINE_JUDGE
  freopen("input.txt", "r", stdin);
  freopen("output.txt", "w", stdout);
#endif
  int T;
  read(T);
  while (T--) {
    int a, b, m, v;
    read(a, b, v, m);
    if (a + b <= m + 1) {
      printf("%d\n", m + 1);
      continue;
    }
    printf("%d\n", solve(a, b, m, v) + solve(b, a, m, v) + 1);
  }
  return 0;
}