网络流
ISAP
cogs885 草地排水
题目大意：赤裸裸的网络流模板题。
#include<iostream> #include<cstdio> using namespace std; int map[201][201]={0},dis[201]={0},gap[201]={0},pre[201]={0}; int sap(int stt,int enn) { int i,y,ans=0,u; bool f=false; gap[0]=enn;u=stt;pre[stt]=stt; while(dis[stt]<enn) { f=false; for (i=1;i<=enn;++i) { if (map[u][i]>0&&dis[u]==dis[i]+1) { f=true; break; } } if (f) { pre[i]=u;u=i; if (u==enn) { y=2100000000; for (i=enn;i!=stt;i=pre[i]) y=min(y,map[pre[i]][i]); ans+=y; for (i=enn;i!=stt;i=pre[i]) { map[pre[i]][i]-=y; map[i][pre[i]]+=y; } u=stt; } } else { --gap[dis[u]];y=enn; if (gap[dis[u]]==0) return ans; for (i=1;i<=enn;++i) if (map[u][i]>0&&dis[i]<y) y=dis[i]; dis[u]=y+1; ++gap[dis[u]]; u=pre[u]; } } return ans; } int main() { freopen("ditch.in","r",stdin); freopen("ditch.out","w",stdout); int n,m,i,j,si,ei,ci; scanf("%d%d",&m,&n); for (i=1;i<=m;++i) { scanf("%d%d%d",&si,&ei,&ci); map[si][ei]+=ci; } printf("%d\n",sap(1,n)); fclose(stdin); fclose(stdout); }
cogs11运输问题1
题目大意：赤裸裸的网络流模板题。
思路：这一版是用的next数组，能处理较多边的情况，节省了空间和时间，不过写的时候总是忘记判断边权是否大于0，所以。。。
#include<iostream> #include<cstdio> using namespace std; struct use{ int st,en,va; }edge[20001]; int point[101]={0},next[20001]={0},pre[101]={0},dis[101]={0},gap[101]={0}; int sap(int stt,int enn) { int i,j,x,y,u,ans=0; bool f=false; gap[0]=enn;u=stt; while(dis[stt]<enn) { f=false;y=point[u]; while (y!=0) { if (dis[u]==dis[edge[y].en]+1&&edge[y].va>0) { f=true;break; } y=next[y]; } if (f) { pre[edge[y].en]=y;u=edge[y].en;y=2100000000; if (u==enn) { for (i=enn;i!=stt;i=edge[pre[i]].st) y=min(y,edge[pre[i]].va); ans+=y; for (i=enn;i!=stt;i=edge[pre[i]].st) { x=(pre[i]-1)^1+1; edge[pre[i]].va-=y; edge[x].va+=y; } u=stt; } } else { --gap[dis[u]]; if (gap[dis[u]]==0) return ans; y=enn; for (i=point[u];i!=0;i=next[i]) if (edge[i].va>0) y=min(y,dis[edge[i].en]); dis[u]=y+1; ++gap[dis[u]]; if (u!=stt) u=edge[pre[u]].st; } } return ans; } int main() { freopen("maxflowa.in","r",stdin); freopen("maxflowa.out","w",stdout); int n,i,j,tot=0,x; scanf("%d",&n); for (i=1;i<=n;++i) for (j=1;j<=n;++j) { scanf("%d",&x); if (x!=0) { ++tot;next[tot]=point[i];point[i]=tot; edge[tot].st=i;edge[tot].en=j;edge[tot].va=x; ++tot;next[tot]=point[j];point[j]=tot; edge[tot].st=j;edge[tot].en=i;edge[tot].va=0; } } printf("%d\n",sap(1,n)); fclose(stdin); fclose(stdout); }
寒假测试 T1
题目大意：n*m的网格内放调料，一个格子上不能放不同颜色的调料（可以重复放一种），有三种放调料的方法：1）放一行上连续几个格子，代价为a；2）放一列上连续几个格子，代价为b；3）单独放一个格子，代价为c。求出放满调料的最小代价和。
思路：在测试的时候直接就跳过了这道题，组里有些搜索的全部超时。这道题的正解是网络流，因为对网络流的理解不够深刻，所以没能很快反应过来。
应该对于读进来的nm矩阵进行预处理，将能横向放的所有格子都找出来（一定是同种颜色在一行上最长的连续子段），将他们与超级源点连边，容量为a；再找纵向的，与超级汇点连边，代价为b；最后将横条和纵条有交点的连边，代价为c。这样我们求出这个网络流的最小割，就是能满足题目要求的最小代价了。其实这样建图不难理解，我们其实就是将一个点放到三种情况里，只要是最小割就一定能填满所有格子，同时保证代价最小。
在实现的时候，用next数组实现的sap，开小了数组（这里最多可能有6n^2的边，包括正反边，而不是3n^2），改了之后才很快的a了。
现在发现网络流中的建模的过程十分复杂，情况很多，以后一定要多练习，多思考，熟练掌握。
#include<cstdio> #include<iostream> #include<cstring> using namespace std; struct use{ int st,en,va; }edge[10000]; int map[40][40]={0},tot,n,m,gap[3000]={0},dis[3000]={0},pre[3000]={0},mapp[40][40][2]={0}, point[3000]={0},next[10000]={0}; void add(int stt,int enn,int vaa) { ++tot;next[tot]=point[stt];point[stt]=tot; edge[tot].st=stt;edge[tot].en=enn;edge[tot].va=vaa; ++tot;next[tot]=point[enn];point[enn]=tot; edge[tot].st=enn;edge[tot].en=stt;edge[tot].va=0; } int sap(int st,int en) { int i,j,u,v,minn,ans=0; bool f; memset(gap,0,sizeof(gap)); memset(dis,0,sizeof(dis)); memset(pre,0,sizeof(pre)); gap[0]=en-st+1;u=st; while (dis[st]<en) { f=false; for (i=point[u];i!=0;i=next[i]) { if (dis[edge[i].en]+1==dis[u]&&edge[i].va>0) { f=true;break; } } if (f) { pre[edge[i].en]=i;u=edge[i].en; if (u==en) { minn=2100000000; for (i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st) { edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; } u=st; } } else { --gap[dis[u]]; if (gap[dis[u]]==0) return ans; minn=en+1; for (i=point[u];i!=0;i=next[i]) if (edge[i].va>0) minn=min(minn,dis[edge[i].en]); dis[u]=minn+1; ++gap[dis[u]]; if (u!=st) u=edge[pre[u]].st; } } return ans; } int main() { freopen("meatchickwing.in","r",stdin); freopen("meatchickwing.out","w",stdout); int t,i,j,a,b,c,x,y,totd,tot1; char ch; scanf("%d",&t); while(t) { memset(map,0,sizeof(map)); memset(edge,0,sizeof(edge)); memset(mapp,0,sizeof(mapp)); memset(edge,0,sizeof(edge)); memset(point,0,sizeof(point)); memset(next,0,sizeof(next)); totd=0;tot=1; scanf("%d%d%d%d%d",&n,&m,&a,&b,&c); for (i=1;i<=n;++i) { for (j=1;j<=m;++j) { cin>>ch; map[i][j]=ch-'a'+1; } } for (i=1;i<=n;++i) for (j=1;j<=m;++j) { if (map[i][j]!=map[i][j-1]) ++totd; mapp[i][j][0]=totd; } tot1=totd; for (j=1;j<=m;++j) for (i=1;i<=n;++i) { if (map[i][j]!=map[i-1][j]) ++totd; mapp[i][j][1]=totd; } for (i=1;i<=tot1;++i) add(0,i,a); for (i=tot1+1;i<=totd;++i) add(i,totd+1,b); for (i=1;i<=n;++i) for (j=1;j<=m;++j) add(mapp[i][j][0],mapp[i][j][1],c); printf("%d\n",sap(0,totd+1)); --t; } fclose(stdin); fclose(stdout); }
cogs14搭配飞行员
题目大意：无源无汇网络流模板题。
思路：对于无源无汇问题，我们只需要加入超级源点和超级汇点，并向对应的点连边，容量为1（一名驾驶员只能安排一次）就可以了。
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; struct use{ int st,en,va; }edge[10000]; int next[10000]={0},point[102]={0},dis[102]={0},pre[102]={0},gap[102]={0},tot; void add(int i,int j,int v) { ++tot;next[tot]=point[i];point[i]=tot; edge[tot].st=i;edge[tot].en=j;edge[tot].va=v; ++tot;next[tot]=point[j];point[j]=tot; edge[tot].st=j;edge[tot].en=i;edge[tot].va=v; } int sap(int stt,int enn) { int i,j,u,v,minn,ans=0; bool f=false; gap[0]=enn-stt+1;u=stt; while(dis[stt]<enn) { f=false; for (i=point[u];i!=0;i=next[i]) if (dis[u]==dis[edge[i].en]+1&&edge[i].va>0) { f=true;break; } if (f) { pre[edge[i].en]=i;u=edge[i].en; if (u==enn) { minn=2100000000; for (i=enn;i!=stt;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=enn;i!=stt;i=edge[pre[i]].st) { edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; } u=stt; } } else { --gap[dis[u]]; if (gap[dis[u]]==0) return ans; minn=enn+1; for (i=point[u];i!=0;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); dis[u]=minn+1; ++gap[dis[u]]; } } return ans; } int main() { int n,m,i,j,a,b; freopen("flyer.in","r",stdin); freopen("flyer.out","w",stdout); tot=1; scanf("%d%d",&n,&m); while(scanf("%d%d",&a,&b)==2) { if (a>b) swap(a,b); add(a,b,1); } for (i=1;i<=m;++i) add(0,i,1); for (i=m+1;i<=n;++i) add(i,n+1,1); printf("%d\n",sap(0,n+1)); fclose(stdin); fclose(stdout); }
cogs12运输问题2
题目大意：有上下界的最大流
思路：建图的时候进行更改，从一条边的起点向终点连一条(x-y)(x为上限，y为下限)的边，从超级源点向终点连一条y的边，从起点向超级汇点连一条y的边，从原图中的汇点向源点连一条正无穷的边（为了使原图为无源无汇的）。做一遍isap，如果从超级源点流出的弧都满载，就是有可行解，这个时候汇点到源点的流量（也就是源点到汇点的残余流量->即edge.va的值）就是流过的下限的流量。删掉超级源汇点，以及汇点向源点连的那条正无穷的边，对源汇点做一遍最大流，与之前下限流量之和就是答案。
#include<iostream> #include<cstdio> #include<cstring> using namespace std; struct use{ int st,en,va; }edge[100001]; int point[202]={0},next[100001]={0},pre[202]={0},dis[202]={0},gap[202]={0},tot=0; int sap(int stt,int enn) { int i,j,x,y,u,ans=0; bool f=false; memset(gap,0,sizeof(gap)); memset(dis,0,sizeof(dis)); memset(pre,0,sizeof(pre)); gap[0]=enn-stt+1;u=stt; while(dis[stt]<enn) { f=false;y=point[u]; while (y!=0) { if (dis[u]==dis[edge[y].en]+1&&edge[y].va>0) { f=true;break; } y=next[y]; } if (f) { pre[edge[y].en]=y;u=edge[y].en; if (u==enn) { y=2100000000; for (i=enn;i!=stt;i=edge[pre[i]].st) y=min(y,edge[pre[i]].va); ans+=y; for (i=enn;i!=stt;i=edge[pre[i]].st) { edge[pre[i]].va-=y; edge[pre[i]^1].va+=y; } u=stt; } } else { --gap[dis[u]]; if (gap[dis[u]]==0) return ans; y=enn+1; for (i=point[u];i!=0;i=next[i]) if (edge[i].va>0) y=min(y,dis[edge[i].en]); dis[u]=y+1; ++gap[dis[u]]; if (u!=stt) u=edge[pre[u]].st; } } return ans; } void add(int i,int j,int v) { ++tot;next[tot]=point[i];point[i]=tot; edge[tot].st=i;edge[tot].en=j;edge[tot].va=v; ++tot;next[tot]=point[j];point[j]=tot; edge[tot].st=j;edge[tot].en=i;edge[tot].va=0; } int main() { freopen("maxflowb.in","r",stdin); freopen("maxflowb.out","w",stdout); int n,i,j,x,y,ans,t=0; bool f=false; scanf("%d",&n); tot=1; for (i=1;i<=n;++i) for (j=1;j<=n;++j) { scanf("%d%d",&y,&x); if (x!=0) { if (y>0) { add(i,j,x-y);add(0,j,y);add(i,n+1,y);t+=y; } else add(i,j,x); } } add(n,1,1000000000); ans=sap(0,n+1); if (ans==t) { ans=edge[tot].va; edge[tot].va=edge[tot-1].va=0; for (i=point[0];i!=0;i=next[i]) edge[i].va=edge[i^1].va=0; for (i=point[n+1];i!=0;i=next[i]) edge[i].va=edge[i^1].va=0; printf("%d\n",sap(1,n)+ans); } else printf("0\n"); fclose(stdin); fclose(stdout); }
cogs28||bzoj1497 最大获利
题目大意：最大权闭合子图模板题
思路：建两排点，由每一个用户群向中转站连有向边，用户群的点权为ci，中转站的点权为-pi。然后就是最大权闭合子图的部分了，从S向正权的点连容量为权的边，从负权向T连容量为|权|的边，原图中的边容量都为正无穷，然后跑最大流，所有正点权和-最大流就是答案了（这里其实是最小割的思路）。
（突然发现自己从来没有用过当前弧cur优化，加了当前弧优化之后，竟然快了。（无）。（数）。（倍）！！！）
#include<iostream> #include<cstdio> #define stan 2100000000LL using namespace std; struct use{ int st,en,va; }edge[500000]; int pp[5001]={0},mi[50001]={0},tot,point[56000]={0},next[500000]={0},dis[56000]={0},gap[56000]={0},pre[56000]={0}, cur[56000]={0},n,m; void add(int stt,int enn,int vaa) { ++tot; next[tot]=point[stt];point[stt]=tot;edge[tot].st=stt;edge[tot].en=enn;edge[tot].va=vaa; ++tot; next[tot]=point[enn];point[enn]=tot;edge[tot].st=enn;edge[tot].en=stt;edge[tot].va=0; } int sap(int stt,int enn) { int u,i,j,ans=0; bool f=false; for (i=1;i<=n+m+1;++i) cur[i]=point[i]; gap[0]=enn-stt+1;u=stt; while(dis[enn]<enn-stt+1) { f=false; for (i=cur[u];i!=0;i=next[i]) { if (dis[edge[i].en]+1==dis[u]&&edge[i].va>0) { cur[u]=i; f=true;break; } } if (f) { pre[edge[i].en]=i;u=edge[i].en; if (u==enn) { j=stan; for (i=u;i!=stt;i=edge[pre[i]].st) j=min(j,edge[pre[i]].va); ans+=j; for (i=u;i!=stt;i=edge[pre[i]].st) { edge[pre[i]].va-=j; edge[pre[i]^1].va+=j; } u=stt; } } else { --gap[dis[u]]; if (gap[dis[u]]==0) return ans; j=stan; for (i=point[u];i!=0;i=next[i]) if (edge[i].va) j=min(j,dis[edge[i].en]); dis[u]=j+1; cur[u]=point[u]; ++gap[dis[u]]; if (u!=stt) u=edge[pre[u]].st; } } return ans; } int main() { freopen("profit.in","r",stdin); freopen("profit.out","w",stdout); int i,j,ai,bi,ci,ans=0; tot=1; scanf("%d%d",&n,&m); for (i=1;i<=n;++i) { scanf("%d",&pp[i]); add(i,n+m+1,pp[i]); } for (i=1;i<=m;++i) { mi[i]=n+i; scanf("%d%d%d",&ai,&bi,&ci); add(0,mi[i],ci);add(mi[i],ai,stan);add(mi[i],bi,stan); ans+=ci; } i=sap(0,n+m+1); ans-=i; printf("%d\n",ans); fclose(stdin); fclose(stdout); }
cogs664 SDOI2010星际竞速
题目大意：貌似是个很像路径覆盖的东西，只是有一些费用，然后求路径覆盖方案中费用最小的。
思路：这里的无向边一定是有向边，毕竟只能从小到大。一开始想不拆点，然后做，但是发现一条路径上的co与流量有关，而流量却不一定为1，所以可能一条路的co加了多遍。就这样卡住了，就这样陷入了死循环。。。后来发现了拆点，因为每一个点都经过一次，所以我们用这个点'表示它经过了，向汇点连边；而它经过的方式有两种，一种是通过之前的点过来，一种是通过跳跃过来，对于跳跃的就是从超级源点跳过来，所以就连出两种边；对于这个点能连出去的话，就用点连向所有的点'，又出现一种边。所有边的容量都为1，费用相应的。。。然后费用流就可以了。（一定要掌握拆点这些神奇的技巧）
#include<iostream> #include<cstdio> #include<cstring> #define len 10000000LL using namespace std; struct use{ int st,en,va,co; }edge[100000]; int que[10000001]={0},a[2000]={0},d[2000]={0},pre[2000]={0},next[100000]={0},point[2000]={0},tot=0,n,m,cost; bool visit[2000]={false}; void add(int stt,int enn,int vaa,int coo) { ++tot;next[tot]=point[stt];point[stt]=tot; edge[tot].st=stt;edge[tot].en=enn;edge[tot].va=vaa;edge[tot].co=coo; ++tot;next[tot]=point[enn];point[enn]=tot; edge[tot].st=enn;edge[tot].en=stt;edge[tot].va=0;edge[tot].co=-coo; } bool work(int stt,int enn) { int head,tail,i,j,x; memset(pre,0,sizeof(pre)); memset(a,127,sizeof(a)); memset(d,127,sizeof(d)); memset(visit,false,sizeof(visit)); head=0;tail=1;que[1]=stt;visit[stt]=true;d[stt]=0; while(head!=tail) { head=head%len+1; x=que[head];visit[x]=false; for (i=point[x];i!=0;i=next[i]) { if (edge[i].va>0&&d[edge[i].en]>d[x]+edge[i].co) { d[edge[i].en]=d[x]+edge[i].co; a[edge[i].en]=min(edge[i].va,a[x]); pre[edge[i].en]=i; if (!visit[edge[i].en]) { visit[edge[i].en]=true; tail=tail%len+1; que[tail]=edge[i].en; } } } } if (d[enn]==d[1999]) return false; cost+=d[enn]*a[enn]; for (i=enn;i!=stt;i=edge[pre[i]].st) { edge[pre[i]].va-=a[enn]; edge[pre[i]^1].va+=a[enn]; } return true; } int main() { freopen("starrace.in","r",stdin); freopen("starrace.out","w",stdout); int n,m,i,j,ai,s,t,wi; tot=1; scanf("%d%d",&n,&m); for (i=1;i<=n;++i) { scanf("%d",&ai); add(0,i,1,0); add(0,i+n,1,ai); add(i+n,n*2+1,1,0); } for (i=1;i<=m;++i) { scanf("%d%d%d",&s,&t,&wi); if (s>t) swap(s,t); add(s,t+n,1,wi); } while(work(0,2*n+1)); printf("%d\n",cost); fclose(stdin); fclose(stdout); }
cogs728最小路径覆盖
题目大意：最小路径覆盖模板题，要输出路径。
思路：题目中竟然给出了建图。。。把每个点都拆成两个，从超级源点向前一个点连边①，从后一个点向汇点连边②，从起点的前一个点向终点的后一个点连边③，容量都是1，然后跑最大流，n-最大流就是答案了（其实最大流就是路径中的那些边的个数）。对于路径来说，每一条流量为0的边③都是路径上的，我们穷举路径的起点，一个路径的起点一定没有没被访问过得别的边③流量为0且终点为起点的后一个点，所以我们找点的时候judge一下，然后从起点往后递归这输出一下就可以了，因为一个点只能有一个终点（只访问一遍），所以不用担心多条路径。
貌似可以用匈牙利算法直接做，小小的学习了一下匈牙利算法（看到一篇博文里说：“匈牙利算法就是‘有机会就上，没机会创造机会上’。”），发现会简单一些。
#include<iostream> #include<cstdio> using namespace std; struct use{ int st,en,va,co; }edge[20000]; int point[500]={0},next[20000]={0},pre[500]={0},dis[500]={0},gap[500]={0},tot,cur[500]={0},n; bool visit[500]={false}; void add(int stt,int enn,int vaa) { ++tot;next[tot]=point[stt];point[stt]=tot; edge[tot].st=stt;edge[tot].en=enn;edge[tot].va=vaa; ++tot;next[tot]=point[enn];point[enn]=tot; edge[tot].st=enn;edge[tot].en=stt;edge[tot].va=0; } int sap(int stt,int enn) { int i,j,u,ans=0; bool f=false; gap[0]=enn-stt+1;u=stt; for (i=stt;i<=enn;++i) cur[i]=point[i]; while(dis[stt]<enn-stt+1) { f=false; for (i=cur[u];i!=0;i=next[i]) { if (edge[i].va>0&&dis[edge[i].en]+1==dis[u]) { cur[u]=i;f=true;break; } } if (f) { pre[edge[i].en]=i;u=edge[i].en; if (u==enn) { j=2100000000; for (i=u;i!=stt;i=edge[pre[i]].st) j=min(j,edge[pre[i]].va); ans+=j; for (i=u;i!=stt;i=edge[pre[i]].st) { edge[pre[i]].va-=j; edge[pre[i]^1].va+=j; } u=stt; } } else { --gap[dis[u]]; if (gap[dis[u]]==0) return ans; j=enn-stt+1; for (i=point[u];i!=0;i=next[i]) if (edge[i].va>0) if (dis[edge[i].en]<j) j=dis[edge[i].en]; dis[u]=j+1;cur[u]=point[u]; ++gap[dis[u]]; if (u!=stt) u=edge[pre[u]].st; } } return ans; } bool judge(int j) { int i; for (i=point[j+n];i!=0;i=next[i]) { if (edge[i].st>0&&edge[i].st<=n) if (!visit[edge[i].st]&&edge[i].va==0) return false; } return true; } void print(int j) { int i; visit[j]=true;printf("%d ",j); for (i=point[j];i!=0;i=next[i]) { if (edge[i].en>n&&edge[i].en<=2*n) if (edge[i].va==0) print(edge[i].en-n); } } int main() { freopen("path3.in","r",stdin); freopen("path3.out","w",stdout); int m,i,j,s,t,ans; tot=1; scanf("%d%d",&n,&m); for (i=1;i<=n;++i) { add(0,i,1);add(i+n,2*n+1,1); } for (i=1;i<=m;++i) { scanf("%d%d",&s,&t); add(s,t+n,1); } ans=n-sap(0,2*n+1); for (i=1;i<=ans;++i) { for (j=1;j<=n;++j) if (!visit[j]&&judge(j)) break; print(j);printf("\n"); } printf("%d\n",ans); fclose(stdin); fclose(stdout); }
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int map[300][300]={0},match[300]={0},go[300]={0}; bool visit[300]={false}; bool find(int i) { int j; for (j=1;j<=map[i][0];++j) { if (!visit[map[i][j]]) { visit[map[i][j]]=true; if (!match[map[i][j]]||find(match[map[i][j]])) { match[map[i][j]]=i;go[i]=map[i][j]; return true; } } } return false; } int main() { freopen("path3.in","r",stdin); freopen("path3.out","w",stdout); int n,m,i,j,s,t,ans=0; scanf("%d%d",&n,&m); for (i=1;i<=m;++i) { scanf("%d%d",&s,&t); ++map[s][0];map[s][map[s][0]]=t; } for (i=1;i<=n;++i) { memset(visit,false,sizeof(visit)); if(!find(i)) ++ans; } for (i=1;i<=n;++i) { if (!match[i]) { j=i; do{ printf("%d ",j); j=go[j]; }while(j); printf("\n"); } } printf("%d\n",ans); fclose(stdin); fclose(stdout); }
cogs738数字梯形
题目大意：找m条路线，分别满足三种条件，并输出最大和（有点像数字三角形）。
思路：根据三种条件建三次图，注意的是这m条路径的起点不能相同，正好m条路径的起点分别为第一行的m个点，然后跑最大费用流就可以了。
#include<iostream> #include<cstdio> #include<cstring> #define len 1000000 using namespace std; struct use{ int st,en,va,co; }edge[10000]={0}; int tot,next[10000]={0},point[5000]={0},dian[21][40][2]={0},map[21][40]={0},que[1000001],dis[5000]={0},a[5000]={0},pre[5000]={0},ans; bool visit[5000]={false}; void add(int st,int en,int va,int co) { ++tot;next[tot]=point[st];point[st]=tot; edge[tot].st=st;edge[tot].en=en;edge[tot].va=va;edge[tot].co=co; ++tot;next[tot]=point[en];point[en]=tot; edge[tot].st=en;edge[tot].en=st;edge[tot].va=0;edge[tot].co=-co; } bool sap(int st,int en) { int head,tail,i,j,x,y; memset(dis,128,sizeof(dis)); memset(a,127,sizeof(a)); memset(visit,false,sizeof(visit)); dis[st]=0;head=0;tail=1;que[1]=st;visit[st]=true; while(head!=tail) { head=head%len+1; x=que[head];visit[x]=false; for (y=point[x];y!=0;y=next[y]) { if (edge[y].va>0&&dis[edge[y].en]<edge[y].co+dis[x]) { dis[edge[y].en]=edge[y].co+dis[x]; a[edge[y].en]=min(a[x],edge[y].va); pre[edge[y].en]=y; if (!visit[edge[y].en]) { visit[edge[y].en]=true;tail=tail%len+1;que[tail]=edge[y].en; } } } } if (dis[en]==dis[0]) return false; ans+=dis[en]*a[en]; for (x=en;x!=st;x=edge[pre[x]].st) { edge[pre[x]].va-=a[en]; edge[pre[x]^1].va+=a[en]; } return true; } int main() { freopen("digit.in","r",stdin); freopen("digit.out","w",stdout); int n,m,i,j,totd=0,enn; scanf("%d%d",&m,&n); totd=2; for (i=1;i<=n;++i) for (j=1;j<m+i;++j) { scanf("%d",&map[i][j]); dian[i][j][0]=++totd;dian[i][j][1]=++totd; } enn=++totd; tot=1;add(1,2,m,0); for (i=1;i<=m;++i) add(2,dian[1][i][0],1,0); for (i=1;i<=n;++i) for (j=1;j<m+i;++j) { add(dian[i][j][0],dian[i][j][1],1,map[i][j]); if (i<n) { add(dian[i][j][1],dian[i+1][j][0],1,0); add(dian[i][j][1],dian[i+1][j+1][0],1,0); } else add(dian[i][j][1],enn,1,0); } ans=0; while(sap(1,enn)); printf("%d\n",ans); memset(next,0,sizeof(next)); memset(point,0,sizeof(point)); memset(edge,0,sizeof(edge)); tot=1;add(1,2,m,0); for (i=1;i<=m;++i) add(2,dian[1][i][0],1,0); for (i=1;i<=n;++i) for (j=1;j<m+i;++j) { add(dian[i][j][0],dian[i][j][1],m,map[i][j]); if (i<n) { add(dian[i][j][1],dian[i+1][j][0],1,0); add(dian[i][j][1],dian[i+1][j+1][0],1,0); } else add(dian[i][j][1],enn,m,0); } ans=0; while(sap(1,enn)); printf("%d\n",ans); memset(next,0,sizeof(next)); memset(point,0,sizeof(point)); memset(edge,0,sizeof(edge)); tot=1;add(1,2,m,0); for (i=1;i<=m;++i) add(2,dian[1][i][0],1,0); for (i=1;i<=n;++i) for (j=1;j<m+i;++j) { add(dian[i][j][0],dian[i][j][1],m,map[i][j]); if (i<n) { add(dian[i][j][1],dian[i+1][j][0],m,0); add(dian[i][j][1],dian[i+1][j+1][0],m,0); } else add(dian[i][j][1],enn,m,0); } ans=0; while(sap(1,enn)); printf("%d\n",ans); fclose(stdin); fclose(stdout); }
cogs396魔术球问题
题目大意：按顺序放入1、2、3...的球在n个柱子上，使相邻的两个球和为完全平方数，问最多能放多少个。
思路：当做贪心来写的。后来明白了怎么跟网络流扯上关系，我们穷举答案，然后将1...ans内能构成相邻的数从小到大连一条边，然后就是最小路径覆盖了，如果路径数<=n就是合理的，找到第一个超过n的ans，ans-1就是答案了，可以用网络流也可以用匈牙利做。不过原题好像要输出方案，不知道是不是要special judge。
（好像看到一个黑心的公式：（n^2+2*n-1）div 2）（自己写的贪心，所以就不贴code了。。。）
cogs729圆桌聚餐
题目大意：m个单位，n张桌子，要求同一单位的人不在同一桌上，如果能安排下就输出1和方案，如果不能就输出0。
思路：最大流的做法。建两排点，从源点向单位连边为单位的人，从桌子向汇点连边为桌子的容量，每个单位向每个桌子连边为1，跑最大流，如果等于所有单位的人数，就是有解，然后找一下残余网络中一二排点之间流量为0的边就是一个安排，然后相应的输出就可以了。
#include<iostream> #include<cstdio> #include<cstring> #define inf 2100000000 using namespace std; struct use{ int st,en,va; }edge[100000]={0}; int ri[151]={0},ci[271]={0},ni[271]={0},next[100000]={0},point[450]={0},cur[450]={0},n,m, gap[450]={0},pre[450]={0},dis[450]={0},tot; void add(int st,int en,int va) { ++tot;next[tot]=point[st];point[st]=tot; edge[tot].st=st;edge[tot].en=en;edge[tot].va=va; ++tot;next[tot]=point[en];point[en]=tot; edge[tot].st=en;edge[tot].en=st;edge[tot].va=0; } int sap(int st,int en) { int i,j,u,ans=0; bool f=false; u=st;gap[0]=en-st+1; for (i=0;i<=n+m+1;++i) cur[i]=point[i]; while(dis[st]<=en-st) { f=false; for (i=cur[u];i;i=next[i]) { if (edge[i].va&&dis[u]==dis[edge[i].en]+1) { cur[u]=i;f=true;break; } } if (f) { pre[edge[i].en]=i;u=edge[i].en; if (u==en) { j=inf; for (i=en;i!=st;i=edge[pre[i]].st) j=min(j,edge[pre[i]].va); ans+=j; for (i=en;i!=st;i=edge[pre[i]].st) { edge[pre[i]].va-=j; edge[pre[i]^1].va+=j; } u=st; } } else { --gap[dis[u]]; if (gap[dis[u]]==0) return ans; j=en-st+1; for (i=point[u];i;i=next[i]) if (edge[i].va) j=min(j,dis[edge[i].en]); dis[u]=j+1;cur[u]=point[u]; ++gap[dis[u]]; if (u!=st) u=edge[pre[u]].st; } } return ans; } int main() { freopen("roundtable.in","r",stdin); freopen("roundtable.out","w",stdout); int i,j,en,summ=0,ans; tot=1; scanf("%d%d",&m,&n); for (i=1;i<=m;++i) { scanf("%d",&ri[i]); summ+=ri[i]; } for (i=1;i<=n;++i) { scanf("%d",&ci[i]); ni[i]=m+i; } en=n+m+1; for (i=1;i<=m;++i) add(0,i,ri[i]); for (i=1;i<=n;++i) add(ni[i],en,ci[i]); for (i=1;i<=m;++i) for (j=1;j<=n;++j) add(i,ni[j],1); ans=sap(0,en); if (ans!=summ) printf("0\n"); else { printf("1\n"); for (i=1;i<=m;++i) { for (j=point[i];j;j=next[j]) if (!edge[j].va) printf("%d ",edge[j].en-m); printf("\n"); } } fclose(stdin); fclose(stdout); }
cogs727太空飞行计划
题目大意：有m项实验，n个器材，已知每个实验的价值和器材的花费，以及每个实验所需要的器材，求可获得的最大价值。
思路：最大权闭合子图。读入比较麻烦，然后就是建图跑最大权闭合子图，最后又是一个麻烦的东西：输出方案。基于以前对最大权闭合子图做法的理解，发现如果一个点和源点的连边仍有流量，就说明这个点在答案的集合里，然后我们就要找到所有这样的点以及他们的器材（dfs了一下，这样能把走过的所有边都找到），然后就是按顺序从小到大输出就可以了。
注意：最近做到一些网络流输出方案的题目，要分析流量和答案之间的关系，然后找到相应的方案。
#include<iostream> #include<cstdio> #include<cstring> #define inf 2100000000 using namespace std; struct use{ int st,en,va; }edge[50000]={0}; int dis[210]={0},gap[210]={0},cur[210]={0},pre[210]={0},ni[101]={0},next[50000]={0},point[210]={0}, exp[101][101]={0},cm[101]={0},cn[101]={0},tot; bool visit[210]={0}; void add(int st,int en,int va) { ++tot;next[tot]=point[st];point[st]=tot; edge[tot].st=st;edge[tot].en=en;edge[tot].va=va; ++tot;next[tot]=point[en];point[en]=tot; edge[tot].st=en;edge[tot].en=st;edge[tot].va=0; } int sap(int st,int en) { int i,j,u,ans=0; bool f=false; for (i=st;i<=en;++i) cur[i]=point[i]; gap[0]=en-st+1;u=st; while(dis[st]<=en-st) { f=false; for (i=cur[u];i;i=next[i]) { if (edge[i].va&&dis[edge[i].en]+1==dis[u]) { f=true;cur[u]=i;break; } } if (f) { pre[edge[i].en]=i;u=edge[i].en; if (u==en) { j=inf; for (i=en;i!=st;i=edge[pre[i]].st) j=min(j,edge[pre[i]].va); ans+=j; for (i=en;i!=st;i=edge[pre[i]].st) { edge[pre[i]].va-=j; edge[pre[i]^1].va+=j; } u=st; } } else { --gap[dis[u]];if (gap[dis[u]]==0) return ans; j=en-st+1; for (i=point[u];i;i=next[i]) if (edge[i].va) j=min(j,dis[edge[i].en]); dis[u]=j+1;++gap[dis[u]];cur[u]=point[u]; if (u!=st) u=edge[pre[u]].st; } } return ans; } void find(int x) { int i,j; visit[x]=true; for (i=point[x];i;i=next[i]) if (edge[i].va&&!visit[edge[i].en]) find(edge[i].en); } int main() { freopen("shuttle.in","r",stdin); freopen("shuttle.out","w",stdout); int n,m,i,j,ans=0,en; char ch; tot=1; scanf("%d%d",&m,&n); for (i=1;i<=m;++i) { scanf("%d",&cm[i]); j=0; while(scanf("%c",&ch)==1) { if (ch=='\r'||ch=='\n') { if (j!=0) { ++exp[i][0];exp[i][exp[i][0]]=j; } break; } if (ch==' '&&j!=0) { ++exp[i][0]; exp[i][exp[i][0]]=j; j=0; } else { if (ch!=' ') j=j*10+ch-'0'; } } } en=n+m+1; for (i=1;i<=n;++i) { scanf("%d",&cn[i]); ni[i]=i+m; } for (i=1;i<=m;++i) { add(0,i,cm[i]);ans+=cm[i]; for (j=1;j<=exp[i][0];++j) add(i,ni[exp[i][j]],inf); } for (i=1;i<=n;++i) add(ni[i],en,cn[i]); ans-=sap(0,en); find(0); for (i=1;i<=m;++i) if (visit[i]) printf("%d ",i); printf("\n"); for (i=1;i<=n;++i) if (visit[ni[i]]) printf("%d ",i); printf("\n%d\n",ans); fclose(stdin); fclose(stdout); }
cogs731最长递增子序列
题目大意：求最长子序列长度，以及原串中能取出多少个（一个元素只能用一遍），当第1个和第n个能用多次的时候能取出多少个。
思路：先dp求出第一个答案（竟然写错了这个交了两遍。。。）然后进行费用流，如果一次增广出的费用等于第一个答案，那么就累加答案，对于第二个和第三个的建图略有不同。第二个当中从源点向每个点、每个点向汇点、每个点向后面>=这个点的点连流量1费用1的边，然后跑最大费用；第三个当中如果是第一个点，就从源点向它连边流量为正无穷，如果为n就向汇点连边流量为正无穷，照样跑。
看到榜上大神的做法：根据第一次dp出来的答案，拆点，连边流量为1，保证一个点只用一次，如果f[i]==1，从s向i连边，如果f[i]==s1，就从i’向t连边，如果f[i]能由f[j]更新，就从j'点向i连边，跑出来的最大流就是第二个答案；在相应的改变流量就是第三个了。
#include<iostream> #include<cstdio> #include<cstring> #define inf 2100000000 #define len 1000000 using namespace std; struct use{ int st,en,va,co; }edge[500000]={0}; int dis[510]={0},a[502]={0},pre[502]={0},next[500000]={0},point[502]={0},aa[501]={0},f[501]={0}, que[1000001]={0},s1=0,tot; bool visit[502]={false}; void add(int st,int en,int va,int co) { ++tot;next[tot]=point[st];point[st]=tot; edge[tot].st=st;edge[tot].en=en;edge[tot].va=va;edge[tot].co=co; ++tot;next[tot]=point[en];point[en]=tot; edge[tot].st=en;edge[tot].en=st;edge[tot].va=0;edge[tot].co=-co; } bool sap(int st,int en,int &ss) { int x,y,head,tail; memset(visit,false,sizeof(visit)); memset(dis,128,sizeof(dis)); dis[st]=0;head=0;tail=1;que[tail]=st;visit[st]=true;a[st]=inf; while(head!=tail) { head=head%len+1; x=que[head];visit[x]=false; for (y=point[x];y;y=next[y]) { if (edge[y].va&&dis[x]+edge[y].co>dis[edge[y].en]) { dis[edge[y].en]=dis[x]+edge[y].co; pre[edge[y].en]=y; a[edge[y].en]=min(a[x],edge[y].va); if (!visit[edge[y].en]) { visit[edge[y].en]=true; tail=tail%len+1;que[tail]=edge[y].en; } } } } if (dis[en]==dis[509]) return false; if (dis[en]==s1) ++ss; for (x=en;x!=st;x=edge[pre[x]].st) { edge[pre[x]].va-=a[en]; edge[pre[x]^1].va+=a[en]; } return true; } int main() { freopen("alis.in","r",stdin); freopen("alis.out","w",stdout); int n,i,j,s2=0,s3=0; scanf("%d",&n); tot=1; for (i=1;i<=n;++i) { scanf("%d",&aa[i]); for (j=1;j<i;++j) if (aa[j]<=aa[i]&&f[j]>=f[i]) f[i]=f[j]; ++f[i]; s1=max(s1,f[i]); } printf("%d\n",s1); for (i=1;i<=n;++i) { add(0,i,1,1); for (j=i+1;j<=n;++j) if (aa[i]<=aa[j]) add(i,j,1,1); add(i,n+1,1,0); } while(sap(0,n+1,s2)); printf("%d\n",s2); memset(next,0,sizeof(next)); memset(point,0,sizeof(point)); tot=1; for (i=1;i<=n;++i) { if (i==1) add(0,i,inf,1); else add(0,i,1,1); for (j=i+1;j<=n;++j) if (aa[i]<=aa[j]) add(i,j,1,1); if (i==n) add(i,n+1,inf,0); else add(i,n+1,1,0); } while(sap(0,n+1,s3)); printf("%d\n",s3); fclose(stdin); fclose(stdout); }
bzoj3993星际战争
题目大意：有n个敌人，m个武器，每种武器有特定的攻击敌人，伤害不同，求最短消灭所有敌人的时间。
思路：因为有小数，我们乘一个1000000，到整数上，然后二分答案，跑网络流（每种武器在二分时间的最多的伤害已知，如果到汇点满流，就是可行）。
注意longlong和int之间一些强转。。。
#include<iostream> #include<cstdio> #include<cstring> #define inf 1000000 #define linf 9223372036854775806LL using namespace std; struct use{ int st,en; long long va; }edge[10000]={0}; int a[100]={0},b[100]={0},tot,map[100][100],bb[100]={0},ba[100]={0},n,m,point[200]={0},next[10000]={0}, gap[200]={0},cur[200]={0},dis[200]={0},pre[200]={0}; void add(int st,int en,long long va) { ++tot;next[tot]=point[st];point[st]=tot; edge[tot].st=st;edge[tot].en=en;edge[tot].va=va; ++tot;next[tot]=point[en];point[en]=tot; edge[tot].st=en;edge[tot].en=st;edge[tot].va=0; } long long sap(int st,int en) { int i,j,u; long long minn,ans=0; bool f=false; memset(gap,0,sizeof(gap)); memset(dis,0,sizeof(dis)); memset(pre,0,sizeof(pre)); gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<en-st+1) { f=false; for (i=cur[u];i;i=next[i]) { if (edge[i].va&&dis[edge[i].en]+1==dis[u]) { f=true;cur[u]=i;break; } } if (f) { pre[edge[i].en]=i;u=edge[i].en; if (u==en) { minn=linf; for (i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st) { edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; } u=st; } } else { --gap[dis[u]]; if (!gap[dis[u]]) return ans; minn=en-st+1; for (i=point[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]<minn) minn=dis[edge[i].en]; cur[u]=point[u]; dis[u]=minn+1;++gap[dis[u]]; if (u!=st) u=edge[pre[u]].st; } } return ans; } bool judge(long long tim,int en) { int i,j; long long sum=0,k; tot=1; memset(point,0,sizeof(point)); memset(next,0,sizeof(next)); for (i=1;i<=m;++i) add(1,bb[i],tim*(long long)b[i]); for (i=1;i<=m;++i) for (j=1;j<=n;++j) if (map[i][j]) add(bb[i],ba[j],linf); for (j=1;j<=n;++j) { add(ba[j],en,(long long)inf*(long long)a[j]); sum+=(long long)inf*(long long)a[j]; } k=sap(1,en); if (k==sum) return true; else return false; } int main() { int i,j,sum=0,minn,en; long long ll,rr,mid; double ans; scanf("%d%d",&n,&m); for (i=1;i<=n;++i) { scanf("%d",&a[i]); sum+=a[i]; ba[i]=m+i+1; } minn=2100000000; for (j=1;j<=m;++j) { scanf("%d",&b[j]); minn=min(minn,b[j]); bb[j]=j+1; } en=2+m+n; for (i=1;i<=m;++i) for (j=1;j<=n;++j) scanf("%d",&map[i][j]); ll=0;rr=(long long)(sum/minn)*(long long)inf; while(ll<rr) { mid=(ll+rr)/2; if (judge(mid,en)) rr=mid; else ll=mid+1; } ans=ll*1.0/inf; printf("%.6f\n",ans); }
cogs410 noi2009植物大战僵尸
题目大意：n*m的方格内有植物，他们可以保护其他植物，也有收益或代价，求收益最大值。
思路：比较明显的最大权闭合子图，但是有一些细节问题。我们按保护关系连边的时候有可能会有环，我们得用拓扑序判一下环。同时有一个隐含条件就是后一列的植物保护同行前一列的植物。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxnode 1000 #define inf 2100000000 using namespace std; int point[maxnode]={0},next[1000000]={0},tot,cur[maxnode]={0},gap[maxnode]={0},dis[maxnode]={0},pre[maxnode]={0}, map[maxnode][maxnode]={0},wi[maxnode],id[50][50]={0},du[maxnode]={0},zhan[maxnode]={0},st[maxnode*2], en[1000000],va[1000000],n,m; bool visit[maxnode]={false}; void add(int stt,int enn,int vaa) { ++tot;next[tot]=point[stt];point[stt]=tot;en[tot]=enn;va[tot]=vaa;st[tot]=stt; ++tot;next[tot]=point[enn];point[enn]=tot;en[tot]=stt;va[tot]=0;st[tot]=enn; } int sap(int stt,int enn) { int i,j,u,ans=0; bool ff; u=stt;gap[0]=enn-stt+1; for (i=0;i<=n+m+1;++i) cur[i]=point[i]; while(dis[stt]<enn-stt+1) { ff=false; for (i=cur[u];i;i=next[i]) { if (va[i]&&dis[en[i]]+1==dis[u]) { ff=true;cur[u]=i;break; } } if (ff) { pre[en[i]]=i;u=en[i]; if (u==enn) { j=inf; for (i=u;i!=stt;i=st[pre[i]]) j=min(j,va[pre[i]]); ans+=j; for (i=u;i!=stt;i=st[pre[i]]) { va[pre[i]]-=j;va[pre[i]^1]+=j; } u=stt; } } else { --gap[dis[u]]; if (!gap[dis[u]]) return ans; j=enn-stt+1; for (i=point[u];i;i=next[i]) if (va[i]&&dis[en[i]]<j) j=dis[en[i]]; dis[u]=j+1;++gap[dis[u]]; cur[u]=point[u]; if (u!=stt) u=st[pre[u]]; } } return ans; } int main() { freopen("pvz.in","r",stdin); freopen("pvz.out","w",stdout); int i,j,k,w,x,y,top=0,sum=0; scanf("%d%d",&n,&m); for (i=0;i<n;++i) for (j=0;j<m;++j) { id[i][j]=i*m+j+1; scanf("%d%d",&wi[id[i][j]],&w); for (k=1;k<=w;++k) { scanf("%d%d",&x,&y); map[id[i][j]][++map[id[i][j]][0]]=x*m+y+1; ++du[x*m+y+1]; } if (j) { map[id[i][j]][++map[id[i][j]][0]]=id[i][j]-1; ++du[id[i][j]-1]; } } for (i=1;i<=n*m;++i) if (!du[i]) zhan[++top]=i; while(top) { i=zhan[top];visit[i]=true;--top; for (j=1;j<=map[i][0];++j) { --du[map[i][j]]; if (!du[map[i][j]]) zhan[++top]=map[i][j]; } } tot=1; for (i=1;i<=n*m;++i) { if (visit[i]) { if (wi[i]>0) { add(0,i,wi[i]);sum+=wi[i]; } if (wi[i]<0) add(i,n*m+1,-wi[i]); } } for (i=1;i<=n*m;++i) for (j=1;j<=map[i][0];++j) if (visit[i]&&visit[map[i][j]]) add(map[i][j],i,inf); printf("%d\n",sum-sap(0,n*m+1)); fclose(stdin); fclose(stdout); }
bzoj3130 费用流
题目大意：给定一个图，求：1）最大流；2）给定可支配费用，求最大的最小费用。
思路：1）是裸的最大流，2）相对复杂。有一个结论：把所有费用放到一条边上，答案最大（怎么证明）。同时我们要把这个费用放在流量最大的边上，那么我们二分所有边的容量中最大的，比这个值大的容量就赋为这个值，跑最大流，如果最大流比1）的小，说明这个值恰好是最大流量的关键值，这个值乘上费用就是答案了。这里要实数二分，整数二分的反例可以从网上找到。
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #define sta 1e-6 #define inf 2100000000 using namespace std; struct use{ int st,en; double va,vv; }edge[2005]={0}; int s,t,point[105]={0},next[2005]={0},dis[105]={0},tot,gap[105]={0},pre[105]={0},cur[105]; void add(int u,int v,int va) { ++tot;next[tot]=point[u];point[u]=tot; edge[tot].st=u;edge[tot].en=v;edge[tot].va=edge[tot].vv=(double)va; ++tot;next[tot]=point[v];point[v]=tot; edge[tot].st=v;edge[tot].en=u;edge[tot].va=edge[tot].vv=(double)0; } int cmp(double a,double b) { if (fabs(a-b)<=sta) return 0; if (a-b>sta) return 1; return -1; } double isap(int st,int en) { int i,j,u; double minn,ans=0; bool f=false; u=st; memset(gap,0,sizeof(gap));gap[0]=en; for (i=st;i<=en;++i) cur[i]=point[i]; memset(dis,0,sizeof(dis)); memset(pre,0,sizeof(pre)); while(dis[en]<en) { f=false; for (i=cur[u];i;i=next[i]) if (dis[edge[i].en]+1==dis[u]&&cmp(edge[i].vv,0)>0) { f=true;cur[u]=i;break; } if (f) { pre[u=edge[i].en]=i; if (u==en) { minn=inf*1.0; for (i=u;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].vv); ans+=minn; for (i=u;i!=st;i=edge[pre[i]].st) { edge[pre[i]].vv-=minn;edge[pre[i]^1].vv+=minn; } u=st; } } else { --gap[dis[u]]; if (gap[dis[u]]==0) return ans; j=inf; for (i=point[u];i;i=next[i]) if (cmp(edge[i].vv,0)>0) j=min(j,dis[edge[i].en]); dis[u]=j+1;++gap[dis[u]];cur[u]=point[u]; if (u!=st) u=edge[pre[u]].st; } } return ans; } int main() { int n,m,p,i,u,v,maxn=0,va; double l,r,mid,ans,j; scanf("%d%d%d",&n,&m,&p);tot=1; for (i=1;i<=m;++i) { scanf("%d%d%d",&u,&v,&va); add(u,v,va);maxn=max(maxn,va); } printf("%d\n",(int)(ans=isap(1,n))); l=0.0;r=maxn*1.0; while(r-l>sta) { mid=(l+r)/2; for (i=2;i<=tot;++i) edge[i].vv=(cmp(edge[i].va,mid)>0 ? mid : edge[i].va); double jj=isap(1,n); if (cmp(ans,jj)==0) r=mid; else l=mid; } printf("%.4f\n",l*(double)p); }
bzoj1266 上学路线
题目大意：给定一张图，求出1~n的最短路，并且求出使最短路变长的最小代价。
思路：跑出最短路图之后，跑最大流就是答案。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxedge 1000010 #define maxnode 1010 #define len 5000000 #define inf 2100000000LL #define LL long long using namespace std; struct use{ int st,en,va; }edge[maxedge]={0}; int point[maxedge]={0},point2[maxedge]={0},next2[maxedge]={0},en2[maxedge]={0},va2[maxedge]={0}, next[maxedge]={0},dis[maxnode]={0},que[len+1]={0},n,tot=0,head,tail,gap[maxnode]={0}, cur[maxnode]={0},pr[maxnode]={0},tt[maxedge]={0}; bool visit[maxnode]={false}; void add2(int u,int v,int va,int j){ next2[++tot]=point2[u];point2[u]=tot;en2[tot]=v;va2[tot]=va;tt[tot]=j; next2[++tot]=point2[v];point2[v]=tot;en2[tot]=u;va2[tot]=va;tt[tot]=j; } void add(int st,int en,int va){ ++tot;next[tot]=point[st];point[st]=tot; edge[tot].st=st;edge[tot].en=en;edge[tot].va=va; ++tot;next[tot]=point[en];point[en]=tot; edge[tot].st=en;edge[tot].en=st;edge[tot].va=0; } void spfa(int st,int en){ int i,j,x;memset(dis,127,sizeof(dis)); head=tail=0;que[++tail]=st;dis[st]=0;visit[st]=true; while(head!=tail){ head=head%len+1;x=que[head];visit[x]=false; for (i=point2[x];i;i=next2[i]){ j=en2[i]; if (dis[j]>dis[x]+va2[i]){ dis[j]=dis[x]+va2[i]; if (!visit[j]){visit[j]=true;tail=tail%len+1;que[tail]=j;} } } } } void pre(){ int i,j;tot=1; for (i=1;i<=n;++i) for (j=point2[i];j;j=next2[j]) if (dis[i]+va2[j]==dis[en2[j]]) add(i,en2[j],tt[j]); } LL sap(int st,int en){ int i,j,u,minn;LL ans=0;bool f; for (i=1;i<=n;++i) cur[i]=point[i]; memset(dis,0,sizeof(dis));gap[0]=en-st+1;u=st; while(dis[st]<en-st+1){ f=false; for (i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ f=true;cur[u]=i;break; } if (f){ pr[edge[i].en]=i;u=edge[i].en; if (u==en){ minn=inf; for (i=u;i!=st;i=edge[pr[i]].st) minn=min(minn,edge[pr[i]].va); ans+=(LL)minn; for (i=u;i!=st;i=edge[pr[i]].st){ edge[pr[i]].va-=minn; edge[pr[i]^1].va+=minn; } u=st; } }else{ --gap[dis[u]];if (!gap[dis[u]]) return ans; minn=en-st+1;cur[u]=point[u]; for (i=point[u];i;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); dis[u]=minn+1;++gap[dis[u]]; if (u!=st) u=edge[pr[u]].st; } }return ans; } int main(){ int m,i,j,u,v,w;LL ans; scanf("%d%d",&n,&m); for (i=1;i<=m;++i){scanf("%d%d%d%d",&u,&v,&w,&j);add2(u,v,w,j);} spfa(1,n);printf("%d\n",dis[n]);pre(); ans=sap(1,n);printf("%I64d\n",ans); }
bzoj3171 循环格
题目大意：每个格点是一个箭头，表示从这里可以到箭头所指方向的邻格，现要求所有点出发都能回到自身最少修改箭头的个数。
思路：考虑最后的图，肯定是很多个环，每个点属于且仅属于一个，所以每个点的出度入度都是1，那么就可以建网络流了，拆点（保证流量），起点到i，流量1价值0；i'到终点，流量1价值0；格点i到四周j'，流量1价值（如果是箭头的方向就是0，否则1），最小费用就是答案了。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxm 500 #define maxe 1000000 #define len 1000000 using namespace std; int point[maxm]={0},next[maxe]={0},en[maxe]={0},va[maxe]={0},co[maxe]={0},tot,bi[maxm][maxm]={0},dx[4]={1,0,-1,0}, dy[4]={0,1,0,-1},dis[maxm]={0},que[len+1]={0},pre[maxm]={0},ai[maxm]={0},map[maxm][maxm]={0},ss,tt,ans, st[maxe]={0}; bool visit[maxm]; char in(){ char ch; while(scanf("%c",&ch)==1) if (ch>='A'&&ch<='Z') return ch; } void add(int u,int v,int vv,int coo){ next[++tot]=point[u];point[u]=tot;st[tot]=u;en[tot]=v;va[tot]=vv;co[tot]=coo; next[++tot]=point[v];point[v]=tot;st[tot]=v;en[tot]=u;va[tot]=0;co[tot]=-coo; } bool spfa(){ int i,j,u,v,head=0,tail=0,sta; memset(visit,false,sizeof(visit)); memset(pre,0,sizeof(pre)); memset(dis,127,sizeof(dis));ai[ss]=sta=dis[0]; que[++tail]=ss;visit[ss]=true;dis[ss]=0; while(head!=tail){ head=head%len+1;u=que[head];visit[u]=false; for (i=point[u];i;i=next[i]){ v=en[i]; if (va[i]&&dis[u]+co[i]<dis[v]){ dis[v]=co[i]+dis[u]; pre[v]=i;ai[v]=min(ai[u],va[i]); if (!visit[v]){ visit[v]=true;tail=tail%len+1;que[tail]=v; } } } }if (dis[tt]==sta) return false; ans+=ai[tt]*dis[tt]; for (i=tt;i!=ss;i=st[pre[i]]){ va[pre[i]]-=ai[tt];va[pre[i]^1]+=ai[tt]; }return true; } int main(){ int n,m,i,j,k,x,y;char ch; scanf("%d%d",&n,&m); for (tot=0,i=1;i<=n;++i) for (j=1;j<=m;++j){ ch=in();bi[i][j]=(tot+=2); if (ch=='R') map[i][j]=1; if (ch=='L') map[i][j]=3; if (ch=='U') map[i][j]=2; if (ch=='D') map[i][j]=0; }ss=0;tt=tot+1;tot=1; for (i=1;i<=n;++i) for (j=1;j<=m;++j){add(ss,bi[i][j]-1,1,0);add(bi[i][j],tt,1,0);} for (i=1;i<=n;++i) for (j=1;j<=m;++j){ for (k=0;k<4;++k){ x=i+dx[k];y=j+dy[k]; if (x==0) x=n;if (x>n) x=1; if (y==0) y=m;if (y>m) y=1; if (map[i][j]==k) add(bi[i][j]-1,bi[x][y],1,0); else add(bi[i][j]-1,bi[x][y],1,1); } }while(spfa()){}; printf("%d\n",ans); }
bzoj2756 奇怪的游戏
题目大意：给定一个n*m的矩阵，每次可以将相邻两个格子同时+1，求最后所有格子上的数一样的最少次数，如果不能一样就输出-1。
思路：对原矩阵黑白染色，每次修改的都是颜色不同的两个块，如果最后高度为height，则有height*num0-sum0=height*num1-sum1(num0、1分别表示黑白的个数；sum0、1分别表示黑白的高度之和)。如果num0!=num1的时候，可以直接解出height（此时就是n*m为奇数），然后网络流判断是否满流就可以了；如果num0==num1（就是n*m为偶数），那么如果height可行、height+1一定可行（构造一下，1×2骨牌覆盖），所以可以二分一下，求出最后的height。关于二分图判断的时候，连边就是从s向所有白点连边，流量为height-map[i][j]；从所有黑点向终点连边，流量也是height-map[i][j]；最后就是白点向黑点连边，流量为正无穷（一定是白向黑，而不是两个方向的）。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxm 50 #define maxe 20000 #define maxx 1605 #define inf 0x7fffffffffffffffLL #define LL long long using namespace std; struct use{ int st,en;LL va; }edge[maxe]; LL map[maxm][maxm]; int point[maxx],next[maxe],tot,bi[maxm][maxm]={0},n,m,dx[4]={1,0,-1,0},dy[4]={0,1,0,-1}, dis[maxx]={0},gap[maxx]={0},pre[maxx]={0},cur[maxx]={0}; void add(int u,int v,LL va){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,va}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0LL}; } LL isap(int ss,int tt){ int i,j,u,v;LL ans=0,minn;bool f; memset(gap,0,sizeof(gap)); memset(pre,0,sizeof(pre)); memset(dis,0,sizeof(dis)); gap[0]=tt-ss+1;u=ss; for (i=ss;i<=tt;++i) cur[i]=point[i]; while(dis[ss]<tt-ss+1){ f=false; for (i=cur[u];i;i=next[i]){ if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ cur[u]=i;f=true;break; } }if (f){ pre[u=edge[i].en]=i; if (u==tt){ minn=inf; for (i=u;i!=ss;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=u;i!=ss;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=ss; } }else{ --gap[dis[u]]; if (!gap[dis[u]]) return ans; j=tt*2;cur[u]=point[u]; for (i=point[u];i;i=next[i]) if (edge[i].va) j=min(j,dis[edge[i].en]); ++gap[dis[u]=j+1]; if (u!=ss) u=edge[pre[u]].st; } }return ans; } bool judge(LL x){ int i,j,k,s,t,xx,yy;LL sum=0LL,ci;tot=1; memset(point,0,sizeof(point)); memset(next,0,sizeof(next)); s=1;t=n*m+2; for (i=1;i<=n;++i) for (j=1;j<=m;++j){ if (map[i][j]>x) return false; if ((i+j)%2){add(bi[i][j],t,x-map[i][j]);sum+=x-map[i][j];} else{ for (k=0;k<4;++k){ xx=i+dx[k];yy=j+dy[k]; if (xx<1||xx>n||yy<1||yy>m) continue; add(bi[i][j],bi[xx][yy],inf); }add(s,bi[i][j],x-map[i][j]); } }return (ci=isap(s,t))==sum; } int main(){ int t,i,j;LL l,r,mid,sum0,sum1,num0,num1; scanf("%d",&t); while(t--){ scanf("%d%d",&n,&m); l=sum0=sum1=num0=num1=0;tot=1; for (i=1;i<=n;++i) for (j=1;j<=m;++j){ scanf("%I64d",&map[i][j]); l=max(l,map[i][j]); if ((i+j)%2){sum1+=map[i][j];++num1;} else {sum0+=map[i][j];++num0;} bi[i][j]=++tot; }if (n*m%2){ if (!judge(l=(sum0-sum1)/(num0-num1))) printf("-1\n"); else printf("%I64d\n",(l*(LL)(n*m)-sum0-sum1)/2); }else{ if (sum0!=sum1) printf("-1\n"); else{ r=inf/n/m; while(l!=r){ mid=(l+r)/2; if (judge(mid)) r=mid; else l=mid+1; }printf("%I64d\n",(l*(LL)(n*m)-sum0-sum1)/2); } } } }
bzoj1934 善意的投票
题目大意：给定n个小朋友，他们之间有m对朋友关系，每个人有一个自己的权值（0/1），统计每个人选0/1时最小矛盾值（朋友之间不同的时候矛盾值+1、每个人和自己初始权值不同时矛盾值+1）。
思路：这是一类网络流问题，可以看作一对点之间的关系。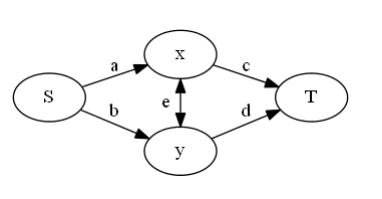
可以列出四个方程，然后相应的建边，这里面的权值只考虑因为朋友间选择不同而产生的代价，所以解出来发现只有x、y间连的是两条流量为1的边，其他都为0。在考虑每个人自己的代价，就是从这个点向S/T连边为1。
（四个方程是：a+b=0(v1)、c+d=0(v2)、a+e+d=1(v3)、b+e+c=1(v4)，会发现e=1((v3+v4-v1-v2)/2)，其他都为0的时候就可以符合了。在有些题目中可能会出现e<0或者e是个小数的情况，都可以相应的变换求解。）
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxm 500 #define maxe 1000000 #define inf 2100000000 using namespace std; struct use{ int st,en,va; }edge[maxe]={0}; int point[maxm]={0},next[maxe]={0},dis[maxm]={0},gap[maxm]={0},pre[maxm]={0},cur[maxm]={0}, ai[maxm]={0},tot,st,en; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0}; } int isap(){ int i,j,u,v,minn,ans=0;bool f=false; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ f=false; for (i=cur[u];i;i=next[i]) if (edge[i].va&&dis[u]==dis[edge[i].en]+1){ cur[u]=i;f=true;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ minn=inf; for (i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ --gap[dis[u]];minn=en-st+1; if (!gap[dis[u]]) return ans; for (i=point[u];i;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); cur[u]=point[u];++gap[dis[u]=minn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } int main(){ int i,j,n,m,u,v;scanf("%d%d",&n,&m); for (en=n+2,st=tot=i=1;i<=n;++i){ scanf("%d",&ai[i]); if (ai[i]) add(st,i+1,1); else add(i+1,en,1); }for (i=1;i<=m;++i){ scanf("%d%d",&u,&v);add(u+1,v+1,1);add(v+1,u+1,1); }printf("%d\n",isap()); }
bzoj2127 happiness
题目大意：给定的n*m的网格中，每个点自己选文/理由不同收益，和相邻的人同时选文/理也有不同收益。
思路：同上，不过这里考虑的是总的收益减去最小割。那么边权就会发生变化，同时因为/2之后是小数，所以要乘2（2a=2aC+abC,2b=2bC+abC,2c=2aM+abM,2d=2bM+abM,2e=abM+abC），尽量将两点间的一起加边，防止tle，同时也是因为在每一个点的边中考虑到了这个点自己选文理的收益，不能重复运算，所以最后加边。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxm 105 #define maxe 1000000 #define inf 2100000000 using namespace std; struct use{ int st,en,va; }edge[maxe]={0}; int point[maxe]={0},next[maxe]={0},dis[maxe]={0},gap[maxe]={0},pre[maxe]={0},cur[maxe]={0}, ai[maxe]={0},tot,st,en,bi[maxm][maxm]={0},map[6][maxm][maxm]={0}; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0}; } int isap(){ int i,j,u,v,minn,ans=0;bool f=false; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ f=false; for (i=cur[u];i;i=next[i]) if (edge[i].va&&dis[u]==dis[edge[i].en]+1){ cur[u]=i;f=true;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ minn=inf; for (i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ --gap[dis[u]];minn=en-st+1; if (!gap[dis[u]]) return ans; for (i=point[u];i;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); cur[u]=point[u];++gap[dis[u]=minn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } int main(){ int i,j,n,m,u,v,sum=0,cnt;scanf("%d%d",&n,&m); st=tot=1;en=n*m+2; for (cnt=i=1;i<=n;++i) for (j=1;j<=m;++j){ bi[i][j]=++cnt; scanf("%d",&map[4][i][j]);sum+=map[4][i][j];map[4][i][j]*=2; } for (i=1;i<=n;++i) for (j=1;j<=m;++j){ scanf("%d",&map[5][i][j]);sum+=map[5][i][j];map[5][i][j]*=2; } for (u=0;u<2;++u) for (i=1;i<n;++i) for (j=1;j<=m;++j){ scanf("%d",&map[u][i][j]);sum+=map[u][i][j]; } for (u=2;u<4;++u) for (i=1;i<=n;++i) for (j=1;j<m;++j){ scanf("%d",&map[u][i][j]);sum+=map[u][i][j]; } for (i=1;i<n;++i) for (j=1;j<=m;++j){ add(bi[i][j],bi[i+1][j],map[0][i][j]+map[1][i][j]); add(bi[i+1][j],bi[i][j],map[0][i][j]+map[1][i][j]); map[4][i][j]+=map[0][i][j]; map[4][i+1][j]+=map[0][i][j]; map[5][i][j]+=map[1][i][j]; map[5][i+1][j]+=map[1][i][j]; } for (i=1;i<=n;++i) for (j=1;j<m;++j){ add(bi[i][j],bi[i][j+1],map[2][i][j]+map[3][i][j]); add(bi[i][j+1],bi[i][j],map[2][i][j]+map[3][i][j]); map[4][i][j]+=map[2][i][j]; map[4][i][j+1]+=map[2][i][j]; map[5][i][j]+=map[3][i][j]; map[5][i][j+1]+=map[3][i][j]; } for (i=1;i<=n;++i) for (j=1;j<=m;++j){ add(st,bi[i][j],map[4][i][j]); add(bi[i][j],en,map[5][i][j]); } printf("%d\n",sum-isap()/2); }
bzoj2039 人员雇佣
题目大意：n个人，每个人有一个代价，如果i、j同时选，可以获得收益2*Eij，如果一个选一个不选就是-Eij。求最大收益。
思路：考虑所有正收益减去最小代价也就是最小割。从s向每个点连边为他的代价，对于一对点间连边Eij*2，对于i到终点就是他所有的可能收益。
#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> #define maxm 1005 #define maxe 5000000 #define inf 0x7fffffffffffffffLL #define LL long long using namespace std; struct use{ int st,en;LL va; }edge[maxe]={0}; int point[maxm]={0},next[maxe]={0},gap[maxm]={0},dis[maxm]={0},pre[maxm]={0},tot,st,en, cur[maxm]={0}; LL ai[maxm]={0}; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0}; } LL isap(){ int i,j,u,v;LL ans=0,minn;bool f; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ f=true;cur[u]=i;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ for (minn=inf,i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ if (!(--gap[dis[u]])) return ans; j=en-st+1; for (i=cur[u]=point[u];i;i=next[i]) if (edge[i].va) j=min(j,dis[edge[i].en]); ++gap[dis[u]=j+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } int main(){ int i,j,n;LL sum=0,x;scanf("%d",&n); st=tot=1;en=n+2; for (i=1;i<=n;++i){ scanf("%I64d",&x);add(st,i+1,x); }for (i=1;i<=n;++i) for (j=1;j<=n;++j){ scanf("%I64d",&x);sum+=x; if (x){ai[i]+=x;add(i+1,j+1,x*2LL);} }for (i=1;i<=n;++i) add(i+1,en,ai[i]); printf("%I64d\n",sum-isap()); }
bzoj1066 蜥蜴
题目大意：给定一个nm的网格，上面有一些柱子和蜥蜴，同时给定可以跳跃的距离d（横、纵坐标差的和，如果从这个柱子可以跳出去就是逃出了），每次有蜥蜴经过柱子会-1，如果柱子高度为0则不存在，不能同时有两个蜥蜴在同一个柱子上，求最少不能逃出的蜥蜴。
思路：建立最大流模型。每个蜥蜴向源点连边流量1，柱子拆点，两点间的流量高度，从一个点的后一个向能到的那个点的前一个连边流量inf，从蜥蜴向所在的柱子前一个连边流量inf，从能跳出的柱子后一个向汇点连边inf。蜥蜴数减去最大流就是答案。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxm 2000 #define maxe 1000000 #define inf 2100000000 using namespace std; struct use{ int st,en,va; }edge[maxe]={0}; int point[maxm]={0},next[maxe]={0},dis[maxm]={0},gap[maxm]={0},pre[maxm]={0},cur[maxm]={0}, ai[maxm]={0},tot,st,en,map[maxm][maxm]={0},hi[maxm][maxm]={0},bi[maxm][maxm]={0}; char in(){ char ch=getchar(); while(true){ if (ch=='.'||ch=='L'||(ch>='0'&&ch<='9')) return ch; ch=getchar(); } } void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0}; } int ab(int x){return x<0?-x:x;} int isap(){ int i,j,u,v,minn,ans=0;bool f=false; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ f=false; for (i=cur[u];i;i=next[i]) if (edge[i].va&&dis[u]==dis[edge[i].en]+1){ cur[u]=i;f=true;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ minn=inf; for (i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ --gap[dis[u]];minn=en-st+1; if (!gap[dis[u]]) return ans; for (i=point[u];i;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); cur[u]=point[u];++gap[dis[u]=minn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } int main(){ int i,j,n,m,u,v,d,a,b,xiyi=0,cnt=0;char ch; scanf("%d%d%d",&n,&m,&d);st=tot=1; for (cnt=i=1;i<=n;++i) for (j=1;j<=m;++j){ ch=in();hi[i][j]=ch-'0'; if (hi[i][j]) bi[i][j]=(cnt+=2); }for (i=1;i<=n;++i) for (j=1;j<=m;++j){ ch=in(); if (ch=='L'){ map[i][j]=++cnt;++xiyi; add(st,cnt,1);add(cnt,bi[i][j]-1,1); } }en=cnt+1; for (i=1;i<=n;++i) for (j=1;j<=m;++j){ if (!hi[i][j]) continue; if (min(i,min(j,min(n-i,m-j)+1))<=d) add(bi[i][j],en,inf); add(bi[i][j]-1,bi[i][j],hi[i][j]); for (a=1;a<=n;++a) for (b=1;b<=m;++b){ if (!hi[a][b]) continue; if (ab(a-i)+ab(b-j)<=d) add(bi[i][j],bi[a][b]-1,inf); } }printf("%d\n",xiyi-isap()); }
bzoj1412 狼和羊的故事
题目大意：给一个nm的网格，其中有羊、狼、空格子，求使狼羊分开的最小的栅栏长度。
思路：从源点向狼连边流量inf，羊向汇点连边流量inf，相邻点之间连边流量1，最小割就是答案。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxm 105 #define maxe 1000000 #define inf 2100000000 using namespace std; struct use{ int st,en,va; }edge[maxe]={0}; int point[maxe]={0},next[maxe]={0},dis[maxe]={0},gap[maxe]={0},pre[maxe]={0},cur[maxe]={0}, ai[maxe]={0},tot,st,en,bi[maxm][maxm]={0},map[maxm][maxm]={0},dx[4]={1,0,-1,0},dy[4]={0,1,0,-1}; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0}; } int isap(){ int i,j,u,v,minn,ans=0;bool f=false; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ f=false; for (i=cur[u];i;i=next[i]) if (edge[i].va&&dis[u]==dis[edge[i].en]+1){ cur[u]=i;f=true;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ minn=inf; for (i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ --gap[dis[u]];minn=en-st+1; if (!gap[dis[u]]) return ans; for (i=point[u];i;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); cur[u]=point[u];++gap[dis[u]=minn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } int main(){ int i,j,n,m,u,v,cnt,k,x,y;scanf("%d%d",&n,&m); st=tot=1;en=n*m+2; for (cnt=i=1;i<=n;++i) for (j=1;j<=m;++j){ scanf("%d",&map[i][j]);bi[i][j]=++cnt; if (map[i][j]==1) add(st,bi[i][j],inf); if (map[i][j]==2) add(bi[i][j],en,inf); } for (i=1;i<=n;++i) for (j=1;j<=m;++j) for (k=0;k<4;++k){ x=i+dx[k];y=j+dy[k]; if (x<1||x>n||y<1||y>m) continue; if (map[i][j]==2||map[x][y]==1) continue; add(bi[i][j],bi[x][y],1); }printf("%d\n",isap()); }
bzoj2561 最小生成树（！！！）
题目大意：给定n个点m条边，再给一条边，求使这条边可能在最大生成树和最小生成树中时，删掉的最少的边数。
思路：考虑求生成树的时候（kruskal算法），如果这条边不能加入，就说明有比它小/大的边联通了起点终点，那么我们对边权小于这条边的建图，最小割就是能使它在最小生成树的条数；最大生成树同理。（一定要分开求解，因为合起来之后可能原本不连通的边连通了，答案就错了。）
注意这里的起点和终点并不是编号最大最小的点，所以isap里面要注意。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxm 20005 #define maxe 1000000 #define inf 2100000000 using namespace std; struct use{ int st,en,va; }edge[maxe]; int point[maxm],next[maxe],dis[maxm],gap[maxm],pre[maxm],cur[maxm],tot,st,en,ui[maxe],vi[maxe],ki[maxe],n; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0}; } int isap(){ int i,j,u,v,minn,ans=0;bool f=false; memset(gap,0,sizeof(gap)); memset(dis,0,sizeof(dis)); memset(pre,0,sizeof(pre)); gap[0]=n;u=st; for (i=1;i<=n;++i) cur[i]=point[i]; while(dis[st]<=n){ f=false; for (i=cur[u];i;i=next[i]) if (edge[i].va&&dis[u]==dis[edge[i].en]+1){ cur[u]=i;f=true;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ minn=inf; for (i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ --gap[dis[u]];minn=n; if (!gap[dis[u]]) return ans; for (i=point[u];i;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); cur[u]=point[u];++gap[dis[u]=minn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } int main(){ int i,j,m,x,ans;scanf("%d%d",&n,&m); for (i=1;i<=m;++i) scanf("%d%d%d",&ui[i],&vi[i],&ki[i]); scanf("%d%d%d",&st,&en,&x); memset(point,0,sizeof(point)); memset(next,0,sizeof(next)); for (tot=i=1;i<=m;++i) if (ki[i]<x){add(ui[i],vi[i],1);add(vi[i],ui[i],1);} ans=isap(); memset(point,0,sizeof(point)); memset(next,0,sizeof(next)); for (tot=i=1;i<=m;++i) if (ki[i]>x){add(ui[i],vi[i],1);add(vi[i],ui[i],1);} ans+=isap();printf("%d\n",ans); }
bzoj3144 切糕
题目大意：给定一个p*q*r(x,y,z轴)的立方体，每个格子都有一个权值，在p*q的每个z轴上选一个点，要求对于向下方投影后相邻的两个格子所选的z轴上的坐标不超过给定的d，求最小权值和。
思路：最小割。首先从每个点向它下面一层的点连边流量权值，从s向第一层连边流量权值，从最后一层向t连边流量inf。然后考虑d的限制，从(x,y,z)向(x,y,z-d)的相邻点连边，就可以保证不会选择超过d的点。
#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> #define maxx 45 #define maxm 100000 #define maxe 2000000 #define inf 2100000000 using namespace std; struct use{ int st,en,va; }edge[maxe]={0}; int point[maxm]={0},next[maxe]={0},gap[maxm]={0},dis[maxm]={0},pre[maxm]={0},tot,st,en, bi[maxx][maxx][maxx]={0},dx[4]={0,1,0,-1},dy[4]={1,0,-1,0},cur[maxm]={0}; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0}; } int isap(){ int i,j,u,v,ans=0,minn;bool f; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ f=true;cur[u]=i;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ for (minn=inf,i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ if (!(--gap[dis[u]])) return ans; minn=en-st+1; for (i=cur[u]=point[u];i;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); ++gap[dis[u]=minn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } int main(){ int i,j,k,t,x,y,p,q,r,d,cnt=0; scanf("%d%d%d%d",&p,&q,&r,&d); st=1;en=p*q*r+2; for (tot=cnt=i=1;i<=r;++i) for (j=1;j<=p;++j) for (k=1;k<=q;++k){ scanf("%d",&x); add((i==1?st:bi[i-1][j][k]),bi[i][j][k]=++cnt,x); if (i>d) for (t=0;t<4;++t){ x=j+dx[t];y=k+dy[t]; if (x<1||x>p||y<1||y>q) continue; add(bi[i][j][k],bi[i-d][x][y],inf); } if (i==r) add(bi[i][j][k],en,inf); }printf("%d\n",isap()); }
bzoj1834 网络扩容
题目大意：给定一张有向图，1）求最大流；2）求流量增大k的最少代价。
思路：1）直接做就可以了流量给定费用0，最大流；2）再把所有边连一边（流量inf费用代价），然后跑费用流，因为有k的限制，所以在费用流中判断一下，如果超了或者要超就return false，同时答案加的不一定是这条增广路的所有流量。
#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> #define maxx 45 #define maxm 1005 #define maxe 1000000 #define inf 2100000000 #define len 1000000 using namespace std; struct use{ int st,en,va,co; }edge[maxe]; int point[maxm]={0},next[maxe]={0},gap[maxm]={0},dis[maxm]={0},pre[maxm]={0},tot,st,en,k, cur[maxm]={0},ui[maxe],vi[maxe],wi[maxe],ci[maxe],anss=0,que[len+1],ai[maxm]={0},flow=0; bool visit[maxm]={false}; void add(int u,int v,int vv,int co){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv,co}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0,-co}; } int isap(){ int i,j,u,v,ans=0,minn;bool f; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ f=true;cur[u]=i;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ for (minn=inf,i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ if (!(--gap[dis[u]])) return ans; minn=en-st+1; for (i=cur[u]=point[u];i;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); ++gap[dis[u]=minn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } bool spfa(){ int i,j,u,v,head=0,tail=0,sta; visit[que[++tail]=st]=true; memset(dis,127,sizeof(dis));dis[st]=0; ai[st]=sta=dis[0]; while(head!=tail){ visit[u=que[head=head%len+1]]=false; for (i=point[u];i;i=next[i]){ if (edge[i].va>0&&dis[v=edge[i].en]>dis[u]+edge[i].co){ dis[v]=dis[u]+edge[i].co; ai[v]=min(ai[u],edge[i].va); pre[edge[i].en]=i; if (!visit[v]) visit[que[tail=tail%len+1]=v]=true; } } }if (dis[en]==sta) return false; if (flow+ai[en]<=k){ flow+=ai[en]; anss+=ai[en]*dis[en]; if (flow==k) return false; }else{ anss+=(k-flow)*dis[en]; return false; }for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=ai[en]; edge[pre[i]^1].va+=ai[en]; }return true; } int main(){ int i,j,n,m;scanf("%d%d%d",&n,&m,&k); st=1;en=n; for (tot=i=1;i<=m;++i){ scanf("%d%d%d%d",&ui[i],&vi[i],&ci[i],&wi[i]); add(ui[i],vi[i],ci[i],0); }printf("%d ",isap()); for (i=1;i<=m;++i) add(ui[i],vi[i],inf,wi[i]); while(spfa());printf("%d\n",anss); }
对k的限制，也可以加一个源点，向1连边为流量k费用0（orz VA）
#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> #define maxx 45 #define maxm 1005 #define maxe 1000000 #define inf 2100000000 #define len 1000000 using namespace std; struct use{ int st,en,va,co; }edge[maxe]; int point[maxm]={0},next[maxe]={0},gap[maxm]={0},dis[maxm]={0},pre[maxm]={0},tot,st,en, cur[maxm]={0},ui[maxe],vi[maxe],wi[maxe],ci[maxe],anss=0,que[len+1],ai[maxm]={0}; bool visit[maxm]={false}; void add(int u,int v,int vv,int co){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv,co}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0,-co}; } int isap(){ int i,j,u,v,ans=0,minn;bool f; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ f=true;cur[u]=i;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ for (minn=inf,i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ if (!(--gap[dis[u]])) return ans; minn=en-st+1; for (i=cur[u]=point[u];i;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); ++gap[dis[u]=minn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } bool spfa(){ int i,j,u,v,head=0,tail=0,sta; visit[que[++tail]=st]=true; memset(dis,127,sizeof(dis));dis[st]=0; ai[st]=sta=dis[0]; while(head!=tail){ visit[u=que[head=head%len+1]]=false; for (i=point[u];i;i=next[i]){ if (edge[i].va>0&&dis[v=edge[i].en]>dis[u]+edge[i].co){ dis[v]=dis[u]+edge[i].co; ai[v]=min(ai[u],edge[i].va); pre[edge[i].en]=i; if (!visit[v]) visit[que[tail=tail%len+1]=v]=true; } } }if (dis[en]==sta) return false; anss+=ai[en]*dis[en]; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=ai[en]; edge[pre[i]^1].va+=ai[en]; }return true; } int main(){ int i,j,n,m,k;scanf("%d%d%d",&n,&m,&k); st=2;en=n+1; for (tot=i=1;i<=m;++i){ scanf("%d%d%d%d",&ui[i],&vi[i],&ci[i],&wi[i]); add(ui[i]+1,vi[i]+1,ci[i],0); }printf("%d ",isap()); add(st=1,2,k,0); for (i=1;i<=m;++i) add(ui[i]+1,vi[i]+1,inf,wi[i]); while(spfa());printf("%d\n",anss); }
bzoj3996 线性代数
题目大意：给定两个矩阵B(n*n)、C(1*n)，D=(A*B-C)*A^T(A^T表示A的转置矩阵（横竖换过来），A是一个1*n的矩阵)，求D的最大值。
思路：D是一个数，是B矩阵里面选中一些1～n中的数，这些行列交叉处的值的和-c中对应的值，所以可以最小割建图（总-最小割=最大值），i、j行S表示选，T表示不选。a+b=0,c+d=bii+bij+bji+bjj,a+e+d=bij+bji+bjj,b+e+c=bij+bji+bii，之后还有从S向每个点连ci的边，解出来后*2，最后/2就可以了。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxm 505 #define maxe 1000000 #define inf 2100000000 using namespace std; struct use{ int st,en,va; }edge[maxe]={0}; int st,en,point[maxm]={0},next[maxe]={0},bi[maxm][maxm],ci[maxm],ev[maxm]={0},cur[maxm]={0}, gap[maxm]={0},dis[maxm]={0},pre[maxm]={0},tot,n; bool visit[maxm]={0}; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0}; } int isap(){ int i,u,ans=0,minn;bool f; u=en;for (i=st;i<=en;++i) cur[i]=point[i]; gap[0]=en-st+1;u=st; while(dis[st]<=en-st+1){ f=false; for (i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[edge[i].st]){ cur[u]=i;f=true;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ minn=inf; for (i=u;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=u;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ --gap[dis[u]];minn=en-st+1; if (!gap[dis[u]]) return ans; cur[u]=point[u]; for (i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]<minn) minn=dis[edge[i].en]; ++gap[dis[u]=minn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } int main(){ int i,j,sum=0;scanf("%d",&n); st=0;en=n+1;tot=1; for (i=1;i<=n;++i) for (j=1;j<=n;++j){ scanf("%d",&bi[i][j]);sum+=bi[i][j]; }for (i=1;i<=n;++i){ scanf("%d",&ci[i]); add(st,i,2*ci[i]); for (j=1;j<=n;++j){ ev[i]+=bi[i][j]+bi[j][i]; if (i!=j) add(i,j,bi[i][j]+bi[j][i]); }add(i,en,ev[i]); }printf("%d\n",sum-isap()/2); }
bzoj1305 跳舞
题目大意：给定n个男孩和女孩，每支舞曲中每个人都要有异性舞伴，同时每对人间只能跳一次，并且与男孩女孩跳舞的不喜欢的人不能超过k个。问最多能跳几只舞。
思路：二分答案+网络流判断。将一个点拆成三个点：一个表示总的、一个是和喜欢的跳、一个是和不喜欢的跳。相应的连边，看最大流是否满流。
注意：二分下界可以设为k，但因为这里二分的是n-l所以下界其实是上界。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxm 305 #define maxe 100005 #define inf 2100000000 using namespace std; struct use{ int st,en,va; }edge[maxe]; int ai[maxm][maxm],n,k,st,en,point[maxm],next[maxe],tot,dis[maxm],gap[maxm],cur[maxm], pre[maxm]; char ch[maxm]; int idx(int i,int x,int y){return i*6-(3-x)*3+y;} void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0}; } int isap(){ int i,j,u,minn,ans=0;bool f; for (i=st;i<=en;++i) cur[i]=point[i]; memset(dis,0,sizeof(dis));u=st; memset(gap,0,sizeof(gap));gap[0]=en-st+1; while(dis[st]<=en-st+1){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ cur[u]=i;f=true;break; } if (f){ pre[u=edge[i].en]=i; if (u==en){ for (minn=inf,i=u;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=u;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ if (!(--gap[dis[u]])) return ans; minn=en-st+1; for (i=cur[u]=point[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]<minn) minn=dis[edge[i].en]; ++gap[dis[u]=minn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans; } bool judge(int x){ int i,j;tot=1;st=0;en=6*n+1; memset(point,0,sizeof(point)); memset(next,0,sizeof(next)); for (i=1;i<=n;++i){ add(st,idx(i,1,1),x); add(idx(i,2,1),en,x); add(idx(i,1,1),idx(i,1,2),k); add(idx(i,2,2),idx(i,2,1),k); add(idx(i,1,1),idx(i,1,3),inf); add(idx(i,2,3),idx(i,2,1),inf); }for (i=1;i<=n;++i) for (j=1;j<=n;++j){ if (ai[i][j]) add(idx(i,1,3),idx(j,2,3),1); else add(idx(i,1,2),idx(j,2,2),1); }if (isap()!=n*x) return false; return true; } int main(){ int i,j,l,r,mid; scanf("%d%d",&n,&k); for (i=1;i<=n;++i){ scanf("%s",ch); for (j=1;j<=n;++j) ai[i][j]=(ch[j-1]=='Y'?1:0); }l=0;r=n; while(l!=r){ mid=(l+r)>>1; if (judge(n-mid)) r=mid; else l=mid+1; }printf("%d\n",n-l); }
贪心的做法是有反例的：
in out
4 1 1
YYNY
NNYN
NNYN
NNYN
bzoj3158 千钧一发
题目大意：给定n个装置，每个有两个权值ai、bi，选出一个集合使得任意i、j(i!=j)满足至少：1）ai^2+aj^2=T^2(T属于N+)；2）gcd(ai,aj)>1。求选出的bi和最大。
思路：对于不能一起出现的连边，拆点后，求最大点权独立集（S向起点连边权值ai，终点向T连边权值ai，起点向终点连边inf），总的和-最小割/2就可以了。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #define N 2005 #define M 3000005 #define LL long long #define inf 2100000000LL using namespace std; struct use{int st,en;LL va;}edge[M]={0}; int tot=0,point[N]={0},next[M],st,en,cur[N],pre[N]={0},dis[N]={0},gap[N]={0}; LL ai[N],bi[N]; void add(int u,int v,LL vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0LL};} LL sqr(LL x){return x*x;} LL gcd(LL x,LL y){return (!y ? x : gcd(y,x%y));} LL isap(){ int i,j,u,v,mn;LL minn,ans=0LL;bool f; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ f=true;cur[u]=i;break;} if (f){ pre[u=edge[i].en]=i; if (u==en){ for (minn=inf,i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ --gap[dis[u]]; if (!gap[dis[u]]) return ans; for (mn=en-st+1,i=cur[u]=point[u];i;i=next[i]) if (edge[i].va) mn=min(mn,dis[edge[i].en]); ++gap[dis[u]=mn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans;} int main(){ int n,i,j;LL x,y,sum=0LL; scanf("%d",&n);st=0;en=2*n+1; for (i=1;i<=n;++i) scanf("%I64d",&ai[i]); for (tot=1,i=1;i<=n;++i){ scanf("%I64d",&bi[i]);sum+=bi[i]; add(st,i,bi[i]);add(i+n,en,bi[i]); }for (i=1;i<=n;++i) for (j=i+1;j<=n;++j){ x=sqr(ai[i])+sqr(ai[j]); if (sqr(sqrt(x))==x&&gcd(ai[i],ai[j])==1){ add(i,j+n,inf);add(j,i+n,inf); } }printf("%I64d\n",sum-isap()/2); }
bzoj2132 圈地计划
题目大意：nm格子建不同功能区收益不同，相邻格子建不同的收益也不同，求最大收益。
思路：因为两个收益都是正的，如果按照一类最小割模型的话，会出现负边权，所以黑白染色后，对于不同颜色的边与源汇点的意义不同（也就是说间不同功能区的收益正好是反着的），相邻的边之间连的就是ci+cj（双向都是这样），然后sum-最小割就可以了。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 10005 #define nn 105 #define M 1000005 #define inf 2100000000 using namespace std; struct use{int st,en,va;}edge[M]; int tot,next[M],point[N]={0},gap[N]={0},dis[N]={0},pre[N],id[nn][nn],st,en,cur[N],ai[nn][nn], bi[nn][nn],ci[nn][nn]; int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0}; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0};} int isap(){ int i,j,u,v,mn,ans=0;bool f; for (i=st;i<=en;++i) cur[i]=point[i]; gap[0]=en-st+1;u=st; while(dis[st]<=en-st+1){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ f=true;cur[u]=i;break;} if (f){ pre[u=edge[i].en]=i; if (u==en){ for (mn=inf,i=en;i!=st;i=edge[pre[i]].st) mn=min(mn,edge[pre[i]].va); ans+=mn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=mn; edge[pre[i]^1].va+=mn; }u=st; } }else{ if (!(--gap[dis[u]])) return ans; for (mn=en-st+1,i=cur[u]=point[u];i;i=next[i]) if (edge[i].va) mn=min(mn,dis[edge[i].en]); ++gap[dis[u]=mn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans;} int main(){ int n,m,i,j,k,x,y,sum=0;scanf("%d%d",&n,&m); st=0;en=n*m+1; for (tot=0,i=1;i<=n;++i) for (j=1;j<=m;++j) id[i][j]=++tot; for (i=1;i<=n;++i) for (j=1;j<=m;++j) scanf("%d",&ai[i][j]); for (i=1;i<=n;++i) for (j=1;j<=m;++j) scanf("%d",&bi[i][j]); for (i=1;i<=n;++i) for (j=1;j<=m;++j) scanf("%d",&ci[i][j]); for (tot=i=1;i<=n;++i) for (j=1;j<=m;++j){ sum+=ai[i][j]+bi[i][j]; if ((i+j)%2){ add(st,id[i][j],ai[i][j]); add(id[i][j],en,bi[i][j]); }else{ add(st,id[i][j],bi[i][j]); add(id[i][j],en,ai[i][j]); }for (k=0;k<4;++k){ x=i+dx[k];y=j+dy[k]; if (x<1||x>n||y<1||y>m) continue; sum+=ci[i][j]; add(id[i][j],id[x][y],ci[i][j]+ci[x][y]); } }printf("%d\n",sum-isap()); }
bzoj1189 紧急疏散
题目大意：给定一个矩阵，X表示墙，.表示空地，D表示门，每块空地上有一个人，每个门每秒可以通过一个人，每块空地上可以站多个人，求最小的所有人都逃离的时间。
思路：二分+isap。先spfa处理出每个人到不同门的最短时间，同时判出无解；然后二分答案，把门拆点（拆500个左右就可以了），然后把相应的人连到能逃出去的门的时间上，判断是否满流就可以了。（一开始二分之后没有拆点，保证不了这个人到了之后可能会排队出去的情况。）
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define up 25 #define N 40000 #define M 4000000 #define inf 2100000000 using namespace std; struct use{int st,en,va;}edge[M]; struct uu{int x1,y1,x2,y2,dd;}que[N+1]; int point[N],next[M],pre[N],gap[N],dis[N],dd[up][up][up][up],tot,n,m,map[up][up],id[up][up], cnt=0,cur[N],st,en,ti[up][up][505]={0},dx[4]={0,1,0,-1},dy[4]={1,0,-1,0}; char ss[N]; bool visit[up][up][up][up]={false}; bool build(){ int i,j,head=0,tail=0,x,y,mn;uu u,v; memset(dd,127,sizeof(dd)); for (i=1;i<=n;++i) for (j=1;j<=m;++j) if (map[i][j]==2){ que[++tail]=(uu){i,j,i,j,0}; visit[i][j][i][j]=true;dd[i][j][i][j]=0;} while(head!=tail){ u=que[head=head%N+1]; visit[u.x1][u.y1][u.x2][u.y2]=false; for (i=0;i<4;++i){ x=u.x2+dx[i];y=u.y2+dy[i]; if (x<1||x>n||y<1||y>m||map[x][y]!=1) continue; if (dd[u.x1][u.y1][x][y]>u.dd+1){ dd[u.x1][u.y1][x][y]=u.dd+1; if (!visit[u.x1][u.y1][x][y]){ que[tail=tail%N+1]=(uu){u.x1,u.y1,x,y,u.dd+1}; visit[u.x1][u.y1][x][y]=true;} } } }for (i=1;i<=n;++i) for (j=1;j<=m;++j){ if (map[i][j]!=1) continue; mn=inf; for (x=1;x<=n;++x) for (y=1;y<=m;++y) if (map[x][y]==2) mn=min(mn,dd[x][y][i][j]); if (mn==inf) return false; }return true;} void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0};} int isap(){ int i,j,u,v,mn,ans=0;bool f; memset(dis,0,sizeof(dis)); memset(gap,0,sizeof(gap)); for (i=st;i<=en;++i) cur[i]=point[i]; gap[0]=en-st+1;u=st; while(dis[st]<=en-st+1){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[edge[i].st]){ f=true;cur[u]=i;break;} if (f){ pre[u=edge[i].en]=i; if (u==en){ for (mn=inf,i=en;i!=st;i=edge[pre[i]].st) mn=min(mn,edge[pre[i]].va); ans+=mn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=mn; edge[pre[i]^1].va+=mn; }u=st; } }else{ if (!(--gap[dis[u]])) return ans; for (mn=en-st+1,cur[u]=i=point[u];i;i=next[i]) if (edge[i].va) mn=min(mn,dis[edge[i].en]); ++gap[dis[u]=mn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans;} bool judge(int x){ int i,j,k,a,b;tot=1; memset(point,0,sizeof(point)); for (i=1;i<=n;++i) for (j=1;j<=m;++j){ if (map[i][j]==1) add(st,id[i][j],1); for (a=1;a<=n;++a) for (b=1;b<=m;++b){ if (map[a][b]!=2) continue; for (k=dd[a][b][i][j];k<=x;++k) add(id[i][j],ti[a][b][k],1); } }for (i=1;i<=n;++i) for (j=1;j<=m;++j){ if (map[i][j]!=2) continue; for (k=1;k<=500;++k) add(ti[i][j][k],en,1); }return (isap()==cnt);} int main(){ int i,j,l,r,mid;scanf("%d%d",&n,&m); for (tot=0,i=1;i<=n;++i){ scanf("%s",ss); for (j=1;j<=m;++j){ map[i][j]=(ss[j-1]=='D' ? 2 : (ss[j-1]=='.')); if (map[i][j]==1) ++cnt; id[i][j]=++tot;} }for (i=1;i<=n;++i) for (j=1;j<=m;++j){ if (map[i][j]!=2) continue; for (l=1;l<=500;++l) ti[i][j][l]=++tot; }st=0;en=++tot; if (!build()) printf("impossible\n"); else{ l=0;r=500; while(l<r){ mid=l+r>>1; if (judge(mid)) r=mid; else l=mid+1; }printf("%d\n",l);} }
bzoj2597 剪刀石头布
题目大意：给定n个人两两游戏的输赢，有些输赢关系未知，问怎么安排两两间的输赢，使得a赢b、b赢c、c赢a的无序三元组abc的个数最多，并输出一个方案。
思路：符合要求的三元组的个数=n(n-1)(n-2)/6-sigma d[i](d[i]-1)/2=n(n-1)(n-2)/6+(sigma d[i] -sigma d[i]^2)/2（容斥原理！！！），所以求出min sigma d[i]^2。对于每个没有确定的二元对建一个点（！！！），S向这个点连流量1费用0，这个点向两个点连边流量1费用0，每个点向T连相应的边。费用=ax^2的费用流可以在(u,v)之间连边流量1、费用a、3a、...、(2k-1)a，最小费用最大流。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 100005 #define up 5005 #define M 1000005 #define inf 2100000000 using namespace std; struct use{int a,b,w,l,r,p;}ai[up]; struct uu{int u,v,va;}ed[M]; struct tree{int l,r;}tr[N]; int point[N]={0},next[M],tot,st,en,dis[N]={0},gap[N]={0},pre[N],cur[N],tt=0,ans=0,root[N]={0}, cc[up],n; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;ed[tot]=(uu){u,v,vv}; next[++tot]=point[v];point[v]=tot;ed[tot]=(uu){v,u,0};} void ask(int id,int i,int l,int r,int ll,int rr){ if (!i) return; if (ll<=l&&r<=rr){add(i+2*n,id+n,inf);return;} int mid=(l+r)>>1; if (ll<=mid) ask(id,tr[i].l,l,mid,ll,rr); if (rr>mid) ask(id,tr[i].r,mid+1,r,ll,rr); } void ins(int id,int la,int &i,int l,int r,int x){ tr[i=++tt].l=tr[la].l;tr[i].r=tr[la].r; if (la) add(la+2*n,i+2*n,inf); add(id,i+2*n,inf); if (l==r) return; int mid=(l+r)>>1; if (x<=mid) ins(id,tr[la].l,tr[i].l,l,mid,x); else ins(id,tr[la].r,tr[i].r,mid+1,r,x); } void isap(){ int i,u,mn;bool f; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ for (f=false,i=cur[u];i;i=next[i]) if (ed[i].va&&dis[u]==dis[ed[i].v]+1){ cur[u]=i;f=true;break; } if (f){ pre[u=ed[i].v]=i; if (u==en){ for (mn=inf,i=en;i!=st;i=ed[pre[i]].u) mn=min(mn,ed[pre[i]].va); ans-=mn; for (i=en;i!=st;i=ed[pre[i]].u){ ed[pre[i]].va-=mn; ed[pre[i]^1].va+=mn; }u=st; } }else{ if (!(--gap[dis[u]])) return; for (mn=en-st+1,cur[u]=i=point[u];i;i=next[i]) if (ed[i].va) mn=min(mn,dis[ed[i].v]); ++gap[dis[u]=mn+1]; if (u!=st) u=ed[pre[u]].u; } } } int main(){ int i,j,a,b,w,l,r,p,sz;scanf("%d",&n); for (tot=i=1;i<=n;++i){ scanf("%d%d%d%d%d%d",&a,&b,&w,&l,&r,&p); ai[i]=(use){a,b,w,l,r,p}; ans+=b+w;cc[i]=a;add(0,i,w);add(i+n,i,p); }sort(cc+1,cc+n+1); sz=unique(cc+1,cc+n+1)-cc-1; for (i=1;i<=n;++i){ ai[i].a=upper_bound(cc+1,cc+sz+1,ai[i].a)-cc-1; j=upper_bound(cc+1,cc+sz+1,ai[i].l)-cc-1; if (cc[j]!=ai[i].l) ++j; ai[i].l=j; ai[i].r=upper_bound(cc+1,cc+sz+1,ai[i].r)-cc-1; if (ai[i].l<=ai[i].r) ask(i,root[i-1],1,sz,ai[i].l,ai[i].r); ins(i,root[i-1],root[i],1,sz,ai[i].a); }st=0;en=tt+2*n+1; for (i=1;i<=n;++i) add(i,en,ai[i].b); isap();printf("%d\n",ans); }
bzoj3218 a + b Problem
题目大意：给定n个连续的格子，已知每个格子染黑、白色的收益。如果格子i是黑色，并且存在j<i，j是白色，li[i]<=ai[j]<=ri[i]，则认为i是奇怪的格子，付出p[i]的代价。问给每个格子染黑或白色，最大收益。
思路：因为是存在就认为奇怪问题，所以不能用文理分科的建图。考虑最小割，S白色，T黑色，每个格子i和i'，S->i边权wi，i->T边权bi，i'->i边权p[i]，如果j能导致i是奇怪格子，就j->i'连边inf。sigma wi+bi -最小割就是答案了。但这样的边是n^2的，所以要优化，因为j<i，所以可以用主席树维护权值的区间，对于一个区间的值可以在线段树上分logn段，边数变为nlogn级别。
注意：主席树每次添加数的时候都要新建节点。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 100005 #define up 5005 #define M 1000005 #define inf 2100000000 using namespace std; struct use{int a,b,w,l,r,p;}ai[up]; struct uu{int u,v,va;}ed[M]; struct tree{int l,r;}tr[N]; int point[N]={0},next[M],tot,st,en,dis[N]={0},gap[N]={0},pre[N],cur[N],tt=0,ans=0,root[N]={0}, cc[up],n; void add(int u,int v,int vv){ //cout<<u<<"->"<<v<<" "<<vv<<endl; next[++tot]=point[u];point[u]=tot;ed[tot]=(uu){u,v,vv}; next[++tot]=point[v];point[v]=tot;ed[tot]=(uu){v,u,0};} void ask(int id,int i,int l,int r,int ll,int rr){ if (!i) return; if (ll<=l&&r<=rr){add(i+2*n,id+n,inf);return;} int mid=(l+r)>>1; if (ll<=mid) ask(id,tr[i].l,l,mid,ll,rr); if (rr>mid) ask(id,tr[i].r,mid+1,r,ll,rr); } void ins(int id,int la,int &i,int l,int r,int x){ tr[i=++tt].l=tr[la].l;tr[i].r=tr[la].r; if (la) add(la+2*n,i+2*n,inf); add(id,i+2*n,inf); if (l==r) return; int mid=(l+r)>>1; if (x<=mid) ins(id,tr[la].l,tr[i].l,l,mid,x); else ins(id,tr[la].r,tr[i].r,mid+1,r,x); } void isap(){ int i,u,mn;bool f; gap[0]=en-st+1;u=st; for (i=st;i<=en;++i) cur[i]=point[i]; while(dis[st]<=en-st+1){ for (f=false,i=cur[u];i;i=next[i]) if (ed[i].va&&dis[u]==dis[ed[i].v]+1){ cur[u]=i;f=true;break; } if (f){ pre[u=ed[i].v]=i; if (u==en){ for (mn=inf,i=en;i!=st;i=ed[pre[i]].u) mn=min(mn,ed[pre[i]].va); ans-=mn; for (i=en;i!=st;i=ed[pre[i]].u){ ed[pre[i]].va-=mn; ed[pre[i]^1].va+=mn; }u=st; } }else{ if (!(--gap[dis[u]])) return; for (mn=en-st+1,cur[u]=i=point[u];i;i=next[i]) if (ed[i].va) mn=min(mn,dis[ed[i].v]); ++gap[dis[u]=mn+1]; if (u!=st) u=ed[pre[u]].u; } } } int main(){ int i,j,a,b,w,l,r,p,sz;scanf("%d",&n); for (tot=i=1;i<=n;++i){ scanf("%d%d%d%d%d%d",&a,&b,&w,&l,&r,&p); ai[i]=(use){a,b,w,l,r,p}; ans+=b+w;cc[i]=a;add(0,i,w);add(i+n,i,p); }sort(cc+1,cc+n+1); sz=unique(cc+1,cc+n+1)-cc-1; for (i=1;i<=n;++i){ ai[i].a=upper_bound(cc+1,cc+sz+1,ai[i].a)-cc-1; j=upper_bound(cc+1,cc+sz+1,ai[i].l)-cc-1; if (cc[j]!=ai[i].l) ++j; ai[i].l=j; ai[i].r=upper_bound(cc+1,cc+sz+1,ai[i].r)-cc-1; if (ai[i].l<=ai[i].r) ask(i,root[i-1],1,sz,ai[i].l,ai[i].r); ins(i,root[i-1],root[i],1,sz,ai[i].a); }st=0;en=tt+2*n+1; for (i=1;i<=n;++i) add(i,en,ai[i].b); isap();printf("%d\n",ans); }
bzoj2965 保护古迹
题目大意：已知平面上p个古迹，n个点间有m条边（保证m条边只会在端点相交，且包含每个古迹的最小多边形是凸多边形），边有边权，求包围至少(!)1～p个古迹的最小代价。
思路：计算几何+最小割。首先dfs出所有的最简多边形（找到两边夹角最大，且相邻两边的叉积正负一样的最小多边形，不会很多）和每个点所在的多边形（判断点在多边形内可以看这个点在所有边的同一侧）。考虑这个平面图的对偶图，对于有共同边的最简多边形连边边权；对于是整个图形外围的边，就从内部那个多边形连向汇点边权。状压选哪些古迹保护，从源点向选中古迹所在的多边形连边inf，最小割就是至少选中状压中点的最小代价。用fi[i]表示保护i这些古迹的时候最小代价，用子集dp一下，更新给gi[i](表示选至少i个古迹保护的最小代价)。gi还要倒着更新一边，最后输出gi就可以了。
这里最简多边形的个数可以根据欧拉公式V(点数)+F(面数)-E(棱数)=2估计一下。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 1005 #define nn 305 #define M 2000005 #define inf 0x7fffffffffffffffLL #define LL long long using namespace std; struct point{LL x,y;}pi[N],ai[N],bi[N][nn]; struct use{int u,v;LL va;point d;}ed[N]; struct uuu{int u,v;LL va;}ee[M]; LL cross(point x,point y){return x.x*y.y-x.y*y.x;} point operator-(point x,point y){return (point){x.x-y.x,x.y-y.y};} point operator+(point x,point y){return (point){x.x+y.x,x.y+y.y};} point operator*(point x,LL y){return (point){x.x*y,x.y*y};} int tot=0,bt=0,bnt[N]={0},p,n,m,zh[N],eg[N][2]={0},point[N]={0},next[N],po1[N]={0},ne1[M],t1, ss,tt,cur[N],dis[N],pre[N],gap[N],tin[nn]; LL fi[N<<1],gi[15]; bool vi[N]={false},hv[nn][nn]={false}; void add(int u,int v,LL vv){ next[++tot]=point[u];point[u]=tot;ed[tot]=(use){u,v,vv,ai[u]-ai[v]}; next[++tot]=point[v];point[v]=tot;ed[tot]=(use){v,u,vv,ai[v]-ai[u]};} void add1(int u,int v,LL vv){ ne1[++t1]=po1[u];po1[u]=t1;ee[t1]=(uuu){u,v,vv}; ne1[++t1]=po1[v];po1[v]=t1;ee[t1]=(uuu){v,u,0LL};} void dfs(int u){ int i,j,k,mj;bool f;vi[u]=true; for (i=point[u];i;i=next[i]){ if (hv[ed[i].v][i]) continue; zh[zh[0]=1]=i;f=true;; while(ed[zh[zh[0]]].v!=u){ for (mj=0,j=point[ed[zh[zh[0]]].v];j;j=next[j]){ if (cross(ed[j].d,ed[zh[zh[0]]].d)>0LL) if (!mj||cross(ed[j].d,ed[mj].d)>0LL) mj=j; }if (!mj){f=false;break;} zh[++zh[0]]=mj; }if (!f) continue; ++bt; for (j=1;j<=zh[0];++j){ bi[bt][++bnt[bt]]=ai[ed[zh[j]].v]; if (!eg[(zh[j]+1)>>1][0]) eg[(zh[j]+1)>>1][0]=bt; else eg[(zh[j]+1)>>1][1]=bt; hv[ed[zh[j]].v][zh[j]]=true; } }for (i=point[u];i;i=next[i]) if (!vi[ed[i].v]) dfs(ed[i].v); } bool judge(int x,int y){ int i,j;LL cc,ci; ci=cross(pi[x]-bi[y][bnt[y]],bi[y][1]-bi[y][bnt[y]]); for (i=2;i<=bnt[y];++i){ cc=cross(pi[x]-bi[y][i-1],bi[y][i]-bi[y][i-1]); if ((ci>0LL&&cc<0LL)||(ci<0LL&&cc>0LL)) return false; }return true;} LL isap(){ int i,j,u,v,mn;LL minn,ans=0LL;bool f; memset(dis,0,sizeof(dis)); memset(gap,0,sizeof(gap));gap[0]=tt-ss+1; for (i=u=ss;i<=tt;++i) cur[i]=po1[i]; while(dis[ss]<=tt-ss+1){ for (f=false,i=cur[u];i;i=ne1[i]) if (ee[i].va&&dis[ee[i].v]+1==dis[u]){ f=true;cur[u]=i;break; } if (f){ pre[u=ee[i].v]=i; if (u==tt){ for (minn=inf,i=tt;i!=ss;i=ee[pre[i]].u) minn=min(minn,ee[pre[i]].va); ans+=minn; for (i=tt;i!=ss;i=ee[pre[i]].u){ ee[pre[i]].va-=minn; ee[pre[i]^1].va+=minn; }u=ss; } }else{ if (!(--gap[dis[u]])) return ans; for (mn=tt-ss+1,cur[u]=i=po1[u];i;i=ne1[i]) if (ee[i].va) mn=min(mn,dis[ee[i].v]); ++gap[dis[u]=mn+1]; if (u!=ss) u=ee[pre[u]].u; } }return ans;} LL calc(int x){ int i,j;t1=1; memset(po1,0,sizeof(po1)); for (i=1;i<=p;++i) if ((1<<(i-1))&x) add1(ss,tin[i],inf); for (i=1;i<=m;++i){ if (!eg[i][0]) continue; if (eg[i][1]){ add1(eg[i][0],eg[i][1],ed[i<<1].va); add1(eg[i][1],eg[i][0],ed[i<<1].va); }else{ add1(eg[i][0],tt,ed[i<<1].va); add1(tt,eg[i][0],ed[i<<1].va); } }return isap();} int main(){ int i,j,u,v;LL vv;scanf("%d%d%d",&p,&n,&m); for (i=1;i<=p;++i) scanf("%I64d%I64d",&pi[i].x,&pi[i].y); for (i=1;i<=n;++i) scanf("%I64d%I64d",&ai[i].x,&ai[i].y); for (i=1;i<=m;++i){ scanf("%d%d%I64d",&u,&v,&vv); add(u,v,vv); }for (i=1;i<=n;++i) if (!vi[i]) dfs(i); ss=0;tt=bt+1; for (i=1;i<=p;++i) for (j=1;j<=bt;++j) if (judge(i,j)){tin[i]=j;break;} memset(fi,127/3,sizeof(fi)); memset(gi,127/3,sizeof(gi)); for (i=1;i<(1<<p);++i){ fi[i]=calc(i); for (j=i;j;j=(j-1)&i) fi[i]=min(fi[i],fi[j]+fi[j^i]); for (u=0,j=i;j;j>>=1) if (j&1) ++u; gi[u]=min(gi[u],fi[i]); }for (i=p-1;i;--i) gi[i]=min(gi[i],gi[i+1]); for (i=1;i<=p;++i) printf("%I64d\n",gi[i]); }
bzoj3438 小M的作物
题目大意：有n个种子，每个种子选A或者B有不同的收益，有m个集合，这些集合里的点同时选A或者B有额外收益。问最大收益。
思路：总的-最小割。对每个种子向S或T连边，流量是收益，表示选A\B。对每个集合拆点，表示都选A\B，从S向前一个连边收益，后一个向汇点连边收益，前后分别向对应的种子连边正无穷。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 3005 #define M 4010000 #define inf 2100000000 using namespace std; struct use{int u,v,va;}ed[M]; int point[N]={0},next[M],cur[N],gap[N]={0},dis[N]={0},pre[N],tot,ss,tt,ai[N],bi[N]; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;ed[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;ed[tot]=(use){v,u,0};} int isap(){ int i,u,mn,ans=0;bool f; for (i=ss;i<=tt;++i) cur[i]=point[i]; gap[0]=tt-ss+1;u=ss; while(dis[ss]<=tt-ss+1){ for (f=false,i=cur[u];i;i=next[i]) if (ed[i].va&&dis[u]==dis[ed[i].v]+1){ f=true;cur[u]=i;break; } if (f){ pre[u=ed[i].v]=i; if (u==tt){ for (mn=inf,i=tt;i!=ss;i=ed[pre[i]].u) mn=min(mn,ed[pre[i]].va); ans+=mn; for (i=tt;i!=ss;i=ed[pre[i]].u){ ed[pre[i]].va-=mn; ed[pre[i]^1].va+=mn; }u=ss;} }else{ if (!(--gap[dis[u]])) return ans; for (mn=tt-ss+1,i=cur[u]=point[u];i;i=next[i]) if (ed[i].va) mn=min(mn,dis[ed[i].v]); ++gap[dis[u]=mn+1]; if (u!=ss) u=ed[pre[u]].u; } }return ans;} int main(){ int i,j,k,x,n,m,sum=0;scanf("%d",&n); for (i=1;i<=n;++i) scanf("%d",&ai[i]); for (i=1;i<=n;++i) scanf("%d",&bi[i]); scanf("%d",&m); ss=0;tt=2*m+n+1; for (tot=i=1;i<=n;++i){ sum+=ai[i]+bi[i]; add(ss,i+2*m,ai[i]); add(i+2*m,tt,bi[i]); }for (i=1;i<=m;++i){ scanf("%d%d%d",&k,&j,&x); add(ss,i,j);add(i+m,tt,x); sum+=j+x; while(k--){ scanf("%d",&x); add(i,x+2*m,inf); add(x+2*m,i+m,inf); } }printf("%d\n",sum-isap()); }
最小割
bzoj2229 最小割
题目大意：给定无向图，求最小割<=x的点对个数。
思路：对于两个不同的最小割，分出来的割集不会出现跨越的情况，也就是说最小割的个数是n级别的，所以可以暴力找n次最小割（分治的思想，每次把一些点划分，然后从一个割集的点中再选点划分，但是这样划分的时候更新的话还是对所有n个点更新）。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 155 #define M 30000 #define inf 4000000000LL #define LL long long using namespace std; struct use{int st,en;LL va;}ed[M],edge[M]; int point[N]={0},next[M]={0},tot,n,m,dis[N],gap[N],pre[N],cur[N],zh[N],bi[N]; LL ci[N][N]; bool visit[N],vi[N]; void add(int u,int v,LL vv){ next[++tot]=point[u];point[u]=tot;ed[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;ed[tot]=(use){v,u,vv};} LL isap(int st,int en){ int i,j,u,v,mn;LL minn,ans=0LL;bool f; memset(gap,0,sizeof(gap)); memset(dis,0,sizeof(dis)); for (i=1;i<=n;++i) cur[i]=point[i]; gap[0]=n;u=st; while(dis[st]<=n){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ f=true;cur[u]=i;break;} if (f){ pre[u=edge[i].en]=i; if (u==en){ for (minn=(LL)inf,i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ if (!(--gap[dis[u]])) return ans; for (mn=n,cur[u]=i=point[u];i;i=next[i]) if (edge[i].va) mn=min(mn,dis[edge[i].en]); ++gap[dis[u]=mn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans;} void dfs(int x){ int i,j;visit[x]=true; for (i=point[x];i;i=next[i]){ if (visit[edge[i].en]||!edge[i].va) continue; dfs(edge[i].en);} } void work(int l,int r){ if (l>=r) return;int i,j;LL t; for (i=2;i<=tot;++i) edge[i]=ed[i]; t=isap(zh[l],zh[r]); memset(visit,false,sizeof(visit)); dfs(zh[l]);bi[0]=0; for (i=1;i<=n;++i){ if (!visit[i]) continue; for (j=1;j<=n;++j){ if (visit[j]) continue; ci[i][j]=min(ci[i][j],t); ci[j][i]=min(ci[j][i],t);} }for (i=l;i<=r;++i) if (visit[zh[i]]) bi[++bi[0]]=zh[i]; for (j=bi[0],i=l;i<=r;++i) if (!visit[zh[i]]) bi[++bi[0]]=zh[i]; for (zh[0]=l-1,i=1;i<=bi[0];++i) zh[++zh[0]]=bi[i]; work(l,l+j-1);work(l+j,r);} int main(){ int t,i,j,u,v,vv,q,x,ans;scanf("%d",&t); while(t--){ memset(point,0,sizeof(point)); memset(ci,0,sizeof(ci)); scanf("%d%d",&n,&m); for (i=1;i<=n;++i) zh[i]=i; for (i=1;i<=m;++i){ scanf("%d%d%d",&u,&v,&vv); ci[u][v]+=(LL)vv;ci[v][u]+=(LL)vv;} for (tot=1,i=1;i<=n;++i) for (j=i+1;j<=n;++j) if (ci[i][j]) add(i,j,ci[i][j]); memset(ci,127,sizeof(ci)); work(1,n);scanf("%d",&q); for (i=1;i<=q;++i){ scanf("%d",&x); for (ans=0,u=1;u<=n;++u) for (v=u+1;v<=n;++v) if (ci[u][v]<=x) ++ans; printf("%d\n",ans); }printf("\n"); } }
bzoj1797 最小割
题目大意：给定有向图，判断每条边是否能出现在某个最小割中和是否一定出现在所有最小割中。
思路：不同的最小割把整个图分成了很多互不相交的部分，这些部分之间的连边就是那些会出现的，而在s和t两部分之间的连边就是一定会出现的，所以跑出最小割之后，找出所有的部分就可以了，如果dfs的话会出现两点间某一条边满流就认为这两个点一个部分的情况，所以可以用tarjan求一下强连通分量，然后进行判断，在判断可能出现的时候是这条边的起始点不在同一个部分并且这条边是从s->t方向的连边（不然两点间反向的边也会被判为能出现）；一定出现的时候就是两部分并且起点在s的部分中、终点在t的部分中。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 4005 #define M 120005 #define inf 2100000000 using namespace std; struct use{int st,en,va;}edge[M],ed[M]; int st,en,point[N]={0},cur[N],next[M],gap[N]={0},dis[N]={0},tot,n,m, zh[N]={0},sccno[N]={0},scnt=0,low[N],pre[N]; void add(int u,int v,int vv){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0};} int isap(){ int i,j,u,v,mn,ans=0;bool f; gap[0]=n;u=st; for (i=1;i<=n;++i) cur[i]=point[i]; while(dis[st]<=n){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[edge[i].st]){ f=true;cur[u]=i;break;} if (f){ pre[u=edge[i].en]=i; if (u==en){ for (mn=inf,i=en;i!=st;i=edge[pre[i]].st) mn=min(mn,edge[pre[i]].va); ans+=mn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=mn; edge[pre[i]^1].va+=mn; }u=st; } }else{ if (!(--gap[dis[u]])) return ans; for (mn=n,cur[u]=i=point[u];i;i=next[i]) if (edge[i].va) mn=min(mn,dis[edge[i].en]); ++gap[dis[u]=mn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans;} void tarjan(int u){ int i,j,v;low[u]=pre[u]=++tot; zh[++zh[0]]=u; for (i=point[u];i;i=next[i]){ if (!edge[i].va) continue; if (!pre[v=edge[i].en]){ tarjan(v);low[u]=min(low[u],low[v]); }else if (!sccno[v]) low[u]=min(low[u],pre[v]); }if (low[u]==pre[u]){ ++scnt; while(zh[0]){ sccno[v=zh[zh[0]--]]=scnt; if (v==u) break; } } } int main(){ int i,j,u,v,vv; scanf("%d%d%d%d",&n,&m,&st,&en); for (tot=i=1;i<=m;++i){ scanf("%d%d%d",&u,&v,&vv);add(u,v,vv); ed[i]=(use){u,v,tot-1}; }isap();memset(pre,0,sizeof(pre)); for (tot=0,i=1;i<=n;++i) if (!pre[i]) tarjan(i); for (i=1;i<=m;++i){ u=ed[i].st;v=ed[i].en; if (sccno[u]!=sccno[v]&&edge[ed[i].va].va==0) printf("1 "); else printf("0 "); if (sccno[u]!=sccno[v]&&sccno[u]==sccno[st]&&sccno[v]==sccno[en]) printf("1\n"); else printf("0\n"); } }
bzoj4519 不同的最小割
题目大意：统计不同数值的最小割个数。
思路:同bzoj2229，用map记录一下。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<map> #define N 855 #define M 30000 #define inf 4000000000LL #define LL long long using namespace std; struct use{int st,en;LL va;}ed[M],edge[M]; int point[N]={0},next[M],tot,n,m,dis[N],gap[N],pre[N],cur[N],zh[N],bi[N],ans=0; LL ci[N][N]; map<LL,bool>cnt; bool visit[N],vi[N]; void add(int u,int v,LL vv){ next[++tot]=point[u];point[u]=tot;ed[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;ed[tot]=(use){v,u,vv};} LL isap(int st,int en){ int i,u,mn;LL minn,ans=0LL;bool f; memset(gap,0,sizeof(gap)); memset(dis,0,sizeof(dis)); for (i=1;i<=n;++i) cur[i]=point[i]; gap[0]=n;u=st; while(dis[st]<=n){ for (f=false,i=cur[u];i;i=next[i]) if (edge[i].va&&dis[edge[i].en]+1==dis[u]){ f=true;cur[u]=i;break;} if (f){ pre[u=edge[i].en]=i; if (u==en){ for (minn=(LL)inf,i=en;i!=st;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; }u=st; } }else{ if (!(--gap[dis[u]])) return ans; for (mn=n,cur[u]=i=point[u];i;i=next[i]) if (edge[i].va) mn=min(mn,dis[edge[i].en]); ++gap[dis[u]=mn+1]; if (u!=st) u=edge[pre[u]].st; } }return ans;} void dfs(int x){ int i;visit[x]=true; for (i=point[x];i;i=next[i]){ if (visit[edge[i].en]||!edge[i].va) continue; dfs(edge[i].en);} } void work(int l,int r){ if (l>=r) return;int i,j;LL t; for (i=2;i<=tot;++i) edge[i]=ed[i]; t=isap(zh[l],zh[r]); if (!cnt[t]){++ans;cnt[t]=true;} memset(visit,false,sizeof(visit)); dfs(zh[l]);bi[0]=0; for (i=l;i<=r;++i) if (visit[zh[i]]) bi[++bi[0]]=zh[i]; for (j=bi[0],i=l;i<=r;++i) if (!visit[zh[i]]) bi[++bi[0]]=zh[i]; for (zh[0]=l-1,i=1;i<=bi[0];++i) zh[++zh[0]]=bi[i]; work(l,l+j-1);work(l+j,r);} int main(){ int i,j,u,v,vv; memset(ci,0,sizeof(ci)); scanf("%d%d",&n,&m); for (i=1;i<=n;++i) zh[i]=i; for (i=1;i<=m;++i){ scanf("%d%d%d",&u,&v,&vv); ci[u][v]+=(LL)vv;ci[v][u]+=(LL)vv;} for (tot=1,i=1;i<=n;++i) for (j=i+1;j<=n;++j) if (ci[i][j]) add(i,j,ci[i][j]); work(1,n);printf("%d\n",ans); }
费用流
cogs14运输问题4
题目大意：最小费用最大流
思路：用spfa做费用的最短路，更新可行流，然后增广就可以了，直到找不到可行流。
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; struct use{ int st,en,va; }edge[10000]; int next[10000]={0},point[102]={0},dis[102]={0},pre[102]={0},gap[102]={0},tot; void add(int i,int j,int v) { ++tot;next[tot]=point[i];point[i]=tot; edge[tot].st=i;edge[tot].en=j;edge[tot].va=v; ++tot;next[tot]=point[j];point[j]=tot; edge[tot].st=j;edge[tot].en=i;edge[tot].va=v; } int sap(int stt,int enn) { int i,j,u,v,minn,ans=0; bool f=false; gap[0]=enn-stt+1;u=stt; while(dis[stt]<enn) { f=false; for (i=point[u];i!=0;i=next[i]) if (dis[u]==dis[edge[i].en]+1&&edge[i].va>0) { f=true;break; } if (f) { pre[edge[i].en]=i;u=edge[i].en; if (u==enn) { minn=2100000000; for (i=enn;i!=stt;i=edge[pre[i]].st) minn=min(minn,edge[pre[i]].va); ans+=minn; for (i=enn;i!=stt;i=edge[pre[i]].st) { edge[pre[i]].va-=minn; edge[pre[i]^1].va+=minn; } u=stt; } } else { --gap[dis[u]]; if (gap[dis[u]]==0) return ans; minn=enn+1; for (i=point[u];i!=0;i=next[i]) if (edge[i].va) minn=min(minn,dis[edge[i].en]); dis[u]=minn+1; ++gap[dis[u]]; } } return ans; } int main() { int n,m,i,j,a,b; tot=1; scanf("%d%d",&n,&m); while(scanf("%d%d",&a,&b)==2) { if (a>b) swap(a,b); add(a,b,1); } for (i=1;i<=m;++i) add(0,i,1); for (i=m+1;i<=n;++i) add(i,n+1,1); printf("%d\n",sap(0,n+1)); }
cogs741负载平衡
题目大意：环状排列的n个仓库，每一个能向相邻两个输送货物，求n个仓库储量一致的时候最小的代价。
思路：延用了之前很多题目的思路，将这些点同化。求出平均数k之后用aa[i]-k，如果>0就从源点连边，如果<0就向汇点连边，流量就是相应的差费用0。相邻的两点之间连边流量正无穷，费用为1。然后跑费用流，就是答案了。（竟然写错了spfa，队首元素取出后一定要标记置反！！！）
#include<iostream> #include<cstdio> #include<cstring> #define len 1000000 #define inf 2100000000 using namespace std; struct use{ int st,en,va,co; }edge[10000]; int dis[110],a[110],pre[110]={0},que[1000001]={0},next[10000]={0},point[110]={0},aa[101]={0},tot,ans=0; bool visit[110]={false}; void add(int st,int en,int va,int co) { ++tot;next[tot]=point[st];point[st]=tot; edge[tot].st=st;edge[tot].en=en;edge[tot].va=va;edge[tot].co=co; ++tot;next[tot]=point[en];point[en]=tot; edge[tot].st=en;edge[tot].en=st;edge[tot].va=0;edge[tot].co=-co; } bool sap(int st,int en) { int x,y,head,tail; memset(visit,false,sizeof(visit)); memset(dis,127,sizeof(dis)); dis[st]=0;head=0;tail=1;que[1]=st;visit[st]=true;a[st]=dis[109]; while(head!=tail) { head=head%len+1; x=que[head];visit[x]=false; for (y=point[x];y;y=next[y]) { if (edge[y].va&&dis[edge[y].en]>dis[x]+edge[y].co) { dis[edge[y].en]=dis[x]+edge[y].co; a[edge[y].en]=min(a[x],edge[y].va); pre[edge[y].en]=y; if (!visit[edge[y].en]) { visit[edge[y].en]=true; tail=tail%len+1;que[tail]=edge[y].en; } } } } if (dis[en]==dis[109]) return false; ans+=dis[en]*a[en]; for (x=en;x!=st;x=edge[pre[x]].st) { edge[pre[x]].va-=a[en]; edge[pre[x]^1].va+=a[en]; } return true; } int main() { int n,i,j,k=0,en; scanf("%d",&n);en=n+1;tot=1; for (i=1;i<=n;++i) { scanf("%d",&aa[i]); k+=aa[i]; } k/=n; for (i=1;i<=n;++i) { aa[i]-=k; if (aa[i]>0) add(0,i,aa[i],0); if (aa[i]<0) add(i,en,-aa[i],0); if (i<n) { add(i,i+1,inf,1);add(i+1,i,inf,1); } else { add(1,n,inf,1);add(n,1,inf,1); } } while(sap(0,en)); printf("%d\n",ans); }
codevs2436修车
题目大意：有m个工人，n个顾客，已知每个工人修相应车的时间，求最少平均等待时间。
思路：建三排点，从超级源点向每个顾客引一条边，容量为1，费用为0；从每个顾客向ci，j（i表示顾客，j表示工人）引一条边，容量为1，费用为0；从每个ci，j向kkj，k（j表示工人，k表示该工人倒数第k顺序修的车）引一条边，容量为1，费用为k*time[i][j]（包括本身共k个人等time[i][j]的时间）；从每个kkj，k向超级汇点引一条边，容量为1，费用为0。从超级源点向超级汇点做费用流，答案就是了。(当然也可以删掉第二排点，然后也可以做出解。)
建图的思路要明确，然后就很简单了。
#include<iostream> #include<cstdio> #include<cstring> #define len 1000000 using namespace std; struct use{ int st,en,va,co; }edge[100000]; int que[1000001]={0},d[2001]={0},pre[2001]={0},a[2001]={0},point[2001]={0},next[100000]={0},flow=0,cost=0, tot,ti[61][10]={0},c[61][10]={0},kk[10][61]={0}; bool visit[2001]={false}; void add(int i,int j,int va,int co) { ++tot;next[tot]=point[i];point[i]=tot; edge[tot].st=i;edge[tot].en=j;edge[tot].va=va;edge[tot].co=co; ++tot;next[tot]=point[j];point[j]=tot; edge[tot].st=j;edge[tot].en=i;edge[tot].va=0;edge[tot].co=-co; } bool work(int s,int t) { int head,tail,u,i,j,stan; memset(visit,false,sizeof(visit)); memset(d,127,sizeof(d));stan=d[0]; memset(a,0,sizeof(a)); memset(pre,0,sizeof(pre)); head=0;tail=1;que[tail]=s;visit[s]=true;d[s]=0;a[s]=stan; while(head!=tail) { head=head%len+1; u=que[head];visit[u]=false; for (i=point[u];i!=0;i=next[i]) { if (edge[i].va>0&&d[edge[i].en]>d[u]+edge[i].co) { d[edge[i].en]=d[u]+edge[i].co; a[edge[i].en]=min(a[u],edge[i].va); pre[edge[i].en]=i; if (!visit[edge[i].en]) { tail=tail%len+1;que[tail]=edge[i].en;visit[edge[i].en]=true; } } } } if (d[t]==stan) return false; flow+=a[t]; cost+=d[t]*a[t]; for (u=t;u!=s;u=edge[pre[u]].st) { edge[pre[u]].va-=a[t]; edge[pre[u]^1].va+=a[t]; } return true; } int main() { int n,m,i,j,k,dian; double ans; scanf("%d%d",&m,&n); tot=1; for (i=1;i<=n;++i) for (j=1;j<=m;++j) scanf("%d",&ti[i][j]); for (i=1;i<=n;++i) add(0,i,1,0); dian=n; for (i=1;i<=n;++i) for (j=1;j<=m;++j) { ++dian; c[i][j]=dian; add(i,dian,1,0); } for (j=1;j<=m;++j) for (k=1;k<=n;++k) { ++dian;kk[j][k]=dian; } for (i=1;i<=n;++i) for (j=1;j<=m;++j) for (k=1;k<=n;++k) { add(c[i][j],kk[j][k],1,k*ti[i][j]); } ++dian; for (j=1;j<=m;++j) for (k=1;k<=n;++k) add(kk[j][k],dian,1,0); while(work(0,dian)); ans=cost*1.0/n; printf("%0.2f\n",ans); }
cogs1366美食节（noi2012）
题目大意：同修车，只是改大了范围，每种菜可能有多道。
思路：同样建三排点，只是源点到第一排点的容量为p[i]，第一排点到第二排点容量为p[i]，其余不变，这样能过6个点，4个tle。
于是有一个优化，对于第三排点，如果倒数第k道菜没选好，那么第k+1道菜也没有安排，所以我们就在每个厨师的第k道菜安排好后，在加第k+1道菜的点和相应的边（每次增广之后。一定要注意加那些边，这里出了好久的问题。。。）
#include<iostream> #include<cstdio> #include<cstring> #define len 100000 using namespace std; struct use{ int st,en,va,co; }edge[1000000]; int que[100001]={0},d[100000]={0},pre[100000]={0},a[100000]={0},point[100000]={0},next[1000000]={0},flow=0,cost=0, tot,ti[41][101]={0},c[41][101]={0},p[41],lev[101]={0},dian,n,m,ji[100000]={0},sum=0,tt; bool visit[100000]={false}; void add(int i,int j,int va,int co) { ++tot;next[tot]=point[i];point[i]=tot; edge[tot].st=i;edge[tot].en=j;edge[tot].va=va;edge[tot].co=co; ++tot;next[tot]=point[j];point[j]=tot; edge[tot].st=j;edge[tot].en=i;edge[tot].va=0;edge[tot].co=-co; } bool work(int s,int t) { int head,tail,u,i,j,stan; memset(visit,false,sizeof(visit)); memset(d,127,sizeof(d));stan=d[0]; head=0;tail=1;que[tail]=s;visit[s]=true;d[s]=0;a[s]=stan; while(head!=tail) { head=head%len+1; u=que[head];visit[u]=false; for (i=point[u];i!=0;i=next[i]) { if (edge[i].va>0&&d[edge[i].en]>d[u]+edge[i].co) { d[edge[i].en]=d[u]+edge[i].co; a[edge[i].en]=min(a[u],edge[i].va); pre[edge[i].en]=i; if (!visit[edge[i].en]) { tail=tail%len+1;que[tail]=edge[i].en;visit[edge[i].en]=true; } } } } if (d[t]==stan) return false; flow+=a[t]; cost+=d[t]*a[t]; for (u=t;u!=s;u=edge[pre[u]].st) { edge[pre[u]].va-=a[t]; edge[pre[u]^1].va+=a[t]; } int cc=ji[edge[pre[t]].st]; ++lev[cc];++dian; ji[dian]=cc; for (i=1;i<=n;++i) add(c[i][cc],dian,1,lev[cc]*ti[i][cc]); add(dian,tt,1,0); return true; } int main() { int i,j,k; scanf("%d%d",&n,&m); tot=1; for (i=1;i<=n;++i) { scanf("%d",&p[i]); sum+=p[i]; } for (i=1;i<=n;++i) for (j=1;j<=m;++j) scanf("%d",&ti[i][j]); for (i=1;i<=n;++i) add(0,i,p[i],0); dian=n; for (i=1;i<=n;++i) for (j=1;j<=m;++j) { ++dian; c[i][j]=dian; add(i,dian,p[i],0); } for (i=1;i<=n;++i) for (j=1;j<=m;++j) { ji[dian+j]=j;lev[j]=1; add(c[i][j],dian+j,1,ti[i][j]); } dian+=m; ++dian; for (j=1;j<=m;++j) add(dian-1-m+j,dian,1,0); tt=dian; while(work(0,tt)); printf("%d\n",cost); }
bzoj1877 SDOI2009晨跑
题目大意：无交叉点的费用流。
思路：拆点，然后就可以保证无交叉点，然后就费用流。。。
#include<iostream> #include<cstdio> #include<cstring> #define len 10000000LL using namespace std; struct use{ int st,en,va,co; }edge[100000]; int next[100000]={0},point[401]={0},pre[401]={0},a[401]={0},d[401]={0},n,m,tot=0,day=0,cost=0,flow=0, que[10000001]={0},qian[201]={0},hou[201]={0}; bool visit[401]={false}; void add(int stt,int enn,int vaa,int coo) { ++tot;next[tot]=point[stt];point[stt]=tot; edge[tot].st=stt;edge[tot].en=enn;edge[tot].va=vaa;edge[tot].co=coo; ++tot;next[tot]=point[enn];point[enn]=tot; edge[tot].st=enn;edge[tot].en=stt;edge[tot].va=0;edge[tot].co=-coo; } bool work(int stt,int enn) { int head,tail,i,j,x; memset(visit,false,sizeof(visit)); memset(d,127,sizeof(d)); memset(a,127,sizeof(a)); memset(pre,0,sizeof(pre)); head=0;tail=1;que[tail]=stt;visit[stt]=true;d[stt]=0; while(head!=tail) { head=head%len+1; x=que[head];visit[x]=false; for (i=point[x];i!=0;i=next[i]) { if (edge[i].va>0&&d[edge[i].en]>d[x]+edge[i].co) { d[edge[i].en]=d[x]+edge[i].co; a[edge[i].en]=min(a[x],edge[i].va); pre[edge[i].en]=i; if (!visit[edge[i].en]) { visit[edge[i].en]=true; tail=tail%len+1; que[tail]=edge[i].en; } } } } if (d[enn]==d[0]) return false; flow+=a[enn]; cost+=a[enn]*d[enn]; for (i=enn;i!=stt;i=edge[pre[i]].st) { edge[pre[i]].va-=a[enn]; edge[pre[i]^1].va+=a[enn]; } return true; } int main() { int i,j,a,b,c; scanf("%d%d",&n,&m); qian[1]=hou[1]=1;qian[n]=hou[n]=2*n-2;tot=1; for (i=2;i<n;++i) { qian[i]=i*2-2;hou[i]=i*2-1; } for (i=2;i<n;++i) add(qian[i],hou[i],1,0); for (i=1;i<=m;++i) { scanf("%d%d%d",&a,&b,&c); add(hou[a],qian[b],1,c); } while(work(qian[1],hou[n])) ++day; printf("%d %d\n",day,cost); }
cogs461餐巾||bzoj1221软件开发
题目大意：我们知道n天里每天需要的毛巾数，我们可以新买毛巾（花费f），也可以把一天用过的毛巾消毒再用（两种方法：要a天的花费fa；要b天的花费fb），然后求满足n天要求的最小花费。
思路：纠结了好久的题目。其实很像之前做过的星际竞速。对于一天的毛巾我们有新毛巾和旧毛巾两排点，为满足新毛巾的要求，我们从源点向这排点连流量正无穷，花费f的边（代表新买的）；从旧毛巾里a+1或b+1天前的点连边为流量正无穷，花费fa或fb的边（代表洗的毛巾）；从新毛巾向汇点连流量ni[i]，花费0的边，满足每天有这么多天毛巾用。为了同时更新旧毛巾，从源点向旧毛巾这排点连流量ni[i]花费0的边，表示这一天用过的毛巾；从上一点的旧毛巾连下来，表示原来的旧毛巾可以留到今天（说成隔几天在洗，遭到了大神的鄙视。。。其实有点像个优化，如果不连这条边的话，就要从这个点向新毛巾里的i+a+1...i+a+j（i+a+j==n）、i+b+1...i+b+j(i+b+j==n)连边了，复杂度将大大提高。）然后跑费用流就可以了。
注意：网络流的构图十分重要，对于很多相似的情况要能熟练应用和理解。
#include<iostream> #include<cstdio> #include<cstring> #define len 1000000 #define inf 2100000000LL using namespace std; struct use{ int st,en,va,co; }edge[10001]={0}; int point[2010]={0},next[10001]={0},dis[2010],a[2010],pre[2010]={0},que[1000001]={0},ni[2010],ans=0,tot; bool visit[2010]={false}; void add(int st,int en,int va,int co) { ++tot;next[tot]=point[st];point[st]=tot; edge[tot].st=st;edge[tot].en=en;edge[tot].va=va;edge[tot].co=co; ++tot;next[tot]=point[en];point[en]=tot; edge[tot].st=en;edge[tot].en=st;edge[tot].va=0;edge[tot].co=-co; } bool work(int st,int en) { int head,tail,x,y; memset(visit,false,sizeof(visit)); memset(dis,127,sizeof(dis)); memset(pre,0,sizeof(pre)); head=0;tail=1;que[tail]=st;visit[st]=true;a[st]=inf;dis[st]=0; while(head!=tail) { head=head%len+1; x=que[head];visit[x]=false; for (y=point[x];y;y=next[y]) { if (edge[y].va&&dis[x]+edge[y].co<dis[edge[y].en]) { dis[edge[y].en]=edge[y].co+dis[x]; pre[edge[y].en]=y; a[edge[y].en]=min(a[x],edge[y].va); if (!visit[edge[y].en]) { visit[edge[y].en]=true; tail=tail%len+1;que[tail]=edge[y].en; } } } } if (dis[en]==dis[2009]) return false; ans+=a[en]*dis[en]; for (x=en;x!=st;x=edge[pre[x]].st) { edge[pre[x]].va-=a[en]; edge[pre[x]^1].va+=a[en]; } return true; } int main() { int n,a,b,f,fa,fb,en,i; scanf("%d",&n); en=2*n+1;tot=1; for (i=1;i<=n;++i) scanf("%d",&ni[i]); scanf("%d%d%d%d%d",&f,&a,&fa,&b,&fb); for (i=1;i<=n;++i) { add(0,i*2-1,inf,f); add(0,i*2,ni[i],0); if (i<n) add(i*2,(i+1)*2,inf,0); if (i+a<=n) add(i*2,(i+a)*2-1,inf,fa); if (i+b<=n) add(i*2,(i+b)*2-1,inf,fb); add(i*2-1,en,ni[i],0); } while(work(0,en)); printf("%d\n",ans); }
bzoj2539 丘比特的烦恼
题目大意：求二分图非完全最大匹配。
思路：费用流就可以了。但是要注意：最大费用最大流！=最大费用可行流，也就是说首先要满足最大流，所以就是找遍所有增广路，代码中spfa找增广的时候，终点的dis不变才是没有增广路。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #define maxm 100 #define maxe 100000 #define LD double #define inf 2100000000 #define eps 1e-8 #define len 100000 using namespace std; struct use{ LD x,y;int l;char s[maxm]; }ai[2][maxm]; struct uu{int st,en,va,co;}ed[maxe]={0}; int point[maxm]={0},next[maxe]={0},dis[maxm]={0},map[maxm][maxm]={0},pre[maxm],aa[maxm], st,en,tot,n,ans=0,que[len]; char s[2][maxm];LD k;bool vi[maxm]; char tch(char x){ if (x>='A'&&x<='Z') return x-'A'+'a'; else return x;} LD sqr(LD x){return x*x;} LD diss(use x,use y){return sqrt(sqr(x.x-y.x)+sqr(x.y-y.y));} void add(int u,int v,int vv,int cc){ next[++tot]=point[u];point[u]=tot;ed[tot]=(uu){u,v,vv,cc}; next[++tot]=point[v];point[v]=tot;ed[tot]=(uu){v,u,0,-cc};} bool scmp(int ki,int l,int k,int i){ int j;if (l!=ai[k][i].l) return false; for (j=0;j<l;++j) if (s[ki][j]!=ai[k][i].s[j]) return false; return true;} int cmp(LD x,LD y){ if (x-y>eps) return 1; if (y-x>eps) return -1; return 0;} bool judge(int a,int b){ int i,j;LD kl=diss(ai[0][a],ai[1][b]); if (kl>k) return false; for (i=1;i<=n;++i){ if (i==a) continue; if (cmp(diss(ai[0][a],ai[0][i])+diss(ai[0][i],ai[1][b]),kl)==0) return false; }for (i=1;i<=n;++i){ if (i==b) continue; if (cmp(diss(ai[0][a],ai[1][i])+diss(ai[1][i],ai[1][b]),kl)==0) return false; }return true; } bool isap(){ int u,v,head=0,tail,i,mn; memset(dis,-60,sizeof(dis));mn=dis[0]; memset(vi,false,sizeof(vi)); aa[st]=inf;dis[st]=0;vi[que[tail=1]=st]=true; while(head!=tail){ vi[u=que[head=head%len+1]]=false; for (i=point[u];i;i=next[i]){ if (ed[i].va&&dis[v=ed[i].en]<dis[u]+ed[i].co){ dis[v]=dis[u]+ed[i].co;pre[v]=i; aa[v]=min(aa[u],ed[i].va); if (!vi[v]) vi[que[tail=tail%len+1]=v]=true; } } }if (dis[en]==mn) return false; ans+=aa[en]*dis[en]; for (i=en;i!=st;i=ed[pre[i]].st){ ed[pre[i]].va-=aa[en]; ed[pre[i]^1].va+=aa[en]; }return true; } int main(){ int i,j,l0,l1,a,b; scanf("%lf%d",&k,&n); st=0;en=2*n+1;tot=1; for (i=1;i<=n;++i){ scanf("%lf%lf%s",&ai[0][i].x,&ai[0][i].y,&ai[0][i].s); ai[0][i].l=strlen(ai[0][i].s); for (j=0;j<ai[0][i].l;++j) ai[0][i].s[j]=tch(ai[0][i].s[j]); add(st,i,1,0); }for (i=1;i<=n;++i){ scanf("%lf%lf%s",&ai[1][i].x,&ai[1][i].y,&ai[1][i].s); ai[1][i].l=strlen(ai[1][i].s); for (j=0;j<ai[1][i].l;++j) ai[1][i].s[j]=tch(ai[1][i].s[j]); add(i+n,en,1,0); }for (i=1;i<=n;++i) for (j=1;j<=n;++j) map[i][j]=1; while(true){ scanf("%s",s[0]);l0=strlen(s[0]); if (l0==3&&s[0][0]=='E'&&s[0][1]=='n'&&s[0][2]=='d') break; scanf("%s%d",s[1],&j);l1=strlen(s[1]); for (i=0;i<l0;++i) s[0][i]=tch(s[0][i]); for (i=0;i<l1;++i) s[1][i]=tch(s[1][i]); for (a=1;a<=n;++a) if (scmp(0,l0,0,a)) break; for (b=1;b<=n;++b) if (scmp(1,l1,1,b)) break; if (a>n||b>n){ for (a=1;a<=n;++a) if (scmp(1,l1,0,a)) break; for (b=1;b<=n;++b) if (scmp(0,l0,1,b)) break; }map[a][b]=j; }for (i=1;i<=n;++i) for (j=1;j<=n;++j){ if (!judge(i,j)) continue; add(i,j+n,1,map[i][j]); }while(isap()); printf("%d\n",ans); }
bzoj1930 吃豆豆
题目大意：给定平面上一些点，有两个人从(0,0)向右或上走（不能相交），问最多能采到多少豆豆。
思路：因为两人路径相交可以通过交换达到要求，所以就是求两个没有公共点的最长不下降序列就可以了。暴力建边跑费用流会mle，考虑减少边，对于三个能组成上升子序列的数，不需要连第一条到第三条的边，但是这样要让每个点能走两次（费用只能+1次的），这样还是会有问题（对拍发现的），还得给不同两点连边的流量也是2。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 4005 #define M 3000000 #define inf 2100000000 using namespace std; struct uu{int x,y;}ai[N]; int cmp(const uu&x,const uu&y){return (x.x==y.x ? x.y<y.y : x.x<y.x);} struct use{int st,en,va,co;}edge[M]; int n,tot,point[N]={0},next[M],dis[N],a[N],pre[N],st,en,ans=0,flow=0,que[N+1]; bool visit[N]={false}; void add(int u,int v,int vv,int co){ next[++tot]=point[u];point[u]=tot;edge[tot]=(use){u,v,vv,co}; next[++tot]=point[v];point[v]=tot;edge[tot]=(use){v,u,0,-co};} void build(){ int i,j,mn;sort(ai+1,ai+n+1,cmp); for (i=1;i<=n;++i){ mn=inf;add(0,i+1,1,0); add(i+n+1,en-1,1,0); add(i+1,i+n+1,1,1);add(i+1,i+n+1,1,0); for (j=i+1;j<=n;++j){ if (ai[j].y>=ai[i].y&&ai[j].y<mn){ add(i+n+1,j+1,2,0);mn=min(mn,ai[j].y);} } } } bool spfa(){ int i,j,u,v,head=0,tail=0; memset(dis,128,sizeof(dis)); visit[que[++tail]=st]=true; dis[st]=0;a[st]=inf; while(head!=tail){ visit[u=que[head=head%N+1]]=false; for (i=point[u];i;i=next[i]) if (edge[i].va&&dis[v=edge[i].en]<dis[u]+edge[i].co){ dis[v]=dis[u]+edge[i].co; pre[v]=i;a[v]=min(a[u],edge[i].va); if (!visit[v]) visit[que[tail=tail%N+1]=v]=true; } }if (dis[en]==dis[N-1]) return false; ans+=dis[en]*a[en];flow+=a[en]; for (i=en;i!=st;i=edge[pre[i]].st){ edge[pre[i]].va-=a[en]; edge[pre[i]^1].va+=a[en]; }return true;} int main(){ int m,i,j;scanf("%d",&n);st=0;en=2*n+3; for (i=1;i<=n;++i) scanf("%d%d",&ai[i].x,&ai[i].y); tot=1;add(0,1,2,0);add(en-1,en,2,0); build();while(spfa()); printf("%d\n",ans); }
bzoj3876 支线剧情
题目大意：给定一个DAG，每条边有费用，求经过所有边至少一次的最小费用。
思路：有下界的最小费用流问题。类比有下界的网络流，可以建超级原汇点S、T，因为题目都是从1开始的，所以从S->1、流量inf费用0；对于每条边u->v，连S->v，流量是下界1费用0，u->v、流量inf费用va，u->T、流量是下界1费用0。这样跑出费用流没有每条边必须经过的那一次，所以还要加上所有边的费用。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 305 #define len 100000 #define M 100000 #define inf 2100000000 using namespace std; struct use{int u,v,va,co;}ed[M]; int point[N]={0},next[M],s,t,tot,ans=0,dis[N],pre[N],ai[N],que[len+1],du[N]={0},zh[N]={0}; bool vi[N]={false}; void add(int u,int v,int vv,int co){ next[++tot]=point[u];point[u]=tot;ed[tot]=(use){u,v,vv,co}; next[++tot]=point[v];point[v]=tot;ed[tot]=(use){v,u,0,-co};} bool spfa(){ int head=0,tail,u,v,i; memset(dis,127,sizeof(dis));dis[s]=0; ai[s]=inf;vi[que[tail=1]=s]=true; while(head!=tail){ vi[u=que[head=head%len+1]]=false; for (i=point[u];i;i=next[i]){ if (ed[i].va&&dis[v=ed[i].v]>dis[u]+ed[i].co){ dis[v]=dis[u]+ed[i].co;pre[v]=i; ai[v]=min(ai[u],ed[i].va); if (!vi[v]) vi[que[tail=tail%len+1]=v]=true; } } }if (dis[t]==dis[N-1]) return false; ans+=dis[t]*ai[t]; for (i=t;i!=s;i=ed[pre[i]].u){ ed[pre[i]].va-=ai[t]; ed[pre[i]^1].va+=ai[t]; }return true;} int main(){ int n,ki,i,j,v,vv;scanf("%d",&n); s=0;t=n+1;tot=1; add(s,1,inf,0); for (i=1;i<=n;++i){ scanf("%d",&ki); for (j=1;j<=ki;++j){ scanf("%d%d",&v,&vv); add(i,v,inf,vv);++du[v]; add(s,v,1,0);add(i,t,1,0); ans+=vv; } }while(spfa());printf("%d\n",ans); }
bzoj2324 营救皮卡丘
题目大意：有k个人，从0号点到所有点，经过i的时候要求先经过1～i-1号点，问k个人走的总路径长度的最小值。
思路：S->0，流量1费用0；i->i'，流量inf、下界1，费用0；i'->j，流量inf，费用是经过小于等于i和j的点的最短路（floyed更新的时候判断一下就可以了！！！）。因为有下界，所以建图同上。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define N 305 #define M 1000005 #define len 1000000 #define inf 2100000000 #define LL long long using namespace std; struct use{int u,v,va;LL co;}ed[M]; int point[N]={0},next[M],pre[N],que[len+1],tot,s,t,n,k,ai[N]; LL ans=0LL,fi[N][N],dis[N]; bool vi[N]={false}; void add(int u,int v,int vv,LL co){ next[++tot]=point[u];point[u]=tot;ed[tot]=(use){u,v,vv,co}; next[++tot]=point[v];point[v]=tot;ed[tot]=(use){v,u,0,-co};} void work(){ int i,j,kk;tot=1; s=0;t=2*n+2; add(s,1,k,0); for (i=1;i<=n;++i){ add(s,i<<1|1,1,0LL); add(i<<1,t,1,0LL); add(i<<1,i<<1|1,inf,0LL); }for (kk=0;kk<=n;++kk) for (i=0;i<=n;++i) for (j=0;j<=n;++j){ if (fi[i][j]>fi[i][kk]+fi[kk][j]) fi[i][j]=fi[i][kk]+fi[kk][j]; if (i<j&&j==kk&&fi[i][j]<fi[N-1][N-1]) add(i<<1|1,j<<1,inf,fi[i][j]); } } bool spfa(){ int i,u,v,head=0,tail; memset(dis,127,sizeof(dis));dis[s]=0LL; ai[s]=inf;vi[que[tail=1]=s]=true; while(head!=tail){ vi[u=que[head=head%len+1]]=false; for (i=point[u];i;i=next[i]) if (ed[i].va&&dis[v=ed[i].v]>dis[u]+ed[i].co){ dis[v]=dis[u]+ed[i].co;pre[v]=i; ai[v]=min(ai[u],ed[i].va); if (!vi[v]) vi[que[tail=tail%len+1]=v]=true; } }if (dis[t]==dis[N-1]) return false; ans+=dis[t]*(LL)ai[t]; for (i=t;i!=s;i=ed[pre[i]].u){ ed[pre[i]].va-=ai[t]; ed[pre[i]^1].va+=ai[t]; }return true;} int main(){ int i,j,m,u,v;LL vv; scanf("%d%d%d",&n,&m,&k); memset(fi,127/3,sizeof(fi)); for (i=1;i<=m;++i){ scanf("%d%d%I64d",&u,&v,&vv); fi[u][v]=fi[v][u]=min(fi[u][v],vv); }work();while(spfa()); printf("%I64d\n",ans); }
bzoj3197 assassin
题目大意：给定一棵树、每个节点当前的状态（0/1）和目标状态，可以重新编号但要求树同构，问从当前状态到目标状态的最小代价。
思路：首先找到重心（两个的时候可以加一个点），树hash。fi[i][j]表示i这个点和j对应时的最小代价，对于hash一样的子树用最佳完美匹配（KM或者费用流）求出fi。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cstdlib> #include<ctime> #define N 705 #define M 1000000 #define UL unsigned long long #define p 971LL #define inf 1000000 #define len 1000000 using namespace std; struct use{int u,v,va,co;}ed[M]; UL th[N],rv[N]; int siz[N],point[N],next[N<<1],en[N<<1],ai[N],bi[N],zh[3]={0},rt,mn,fi[N][N],gi[N<<1]={0}, ss,tt,po1[N<<1]={0},ne1[M],tot,n,dis[N<<1],pre[N<<1],aa[N<<1],que[len+1],flow,cost, ci[N<<1]; bool fb[N<<1]={0},vi[N<<1]; void add(int u,int v){ next[++tot]=point[u];point[u]=tot;en[tot]=v; next[++tot]=point[v];point[v]=tot;en[tot]=u;} void getrt(int u,int ff){ int i,v,mz=0;siz[u]=1; for (i=point[u];i;i=next[i]){ if ((v=en[i])==ff||fb[i]) continue; getrt(v,u);siz[u]+=siz[v]; mz=max(mz,siz[v]); }mz=max(mz,n-siz[u]); if (mz<=mn){ if (mz==mn&&zh[0]<=1) zh[++zh[0]]=u; else{mn=mz;zh[zh[0]=1]=u;} } } void geth(int u,int ff){ int i,v;siz[u]=1;th[u]=0LL; for (i=point[u];i;i=next[i]){ if ((v=en[i])==ff||fb[i]) continue; geth(v,u);th[u]+=th[v];siz[u]+=siz[v]; }th[u]=(rv[siz[u]]*p)^th[u]; } void add1(int u,int v,int va,int co){ if (gi[u]!=mn) gi[ci[++ci[0]]=u]=mn; if (gi[v]!=mn) gi[ci[++ci[0]]=v]=mn; ne1[++tot]=po1[u];po1[u]=tot;ed[tot]=(use){u,v,va,co}; ne1[++tot]=po1[v];po1[v]=tot;ed[tot]=(use){v,u,0,-co};} bool spfa(){ int u,head=0,tail,i,v; for (i=1;i<=ci[0];++i){ dis[ci[i]]=inf;vi[ci[i]]=false; }dis[que[tail=1]=ss]=0; aa[ss]=inf;vi[ss]=true; while(head!=tail){ vi[u=que[head=head%len+1]]=false; for (i=po1[u];i;i=ne1[i]) if (ed[i].va&&dis[v=ed[i].v]>dis[u]+ed[i].co){ dis[v]=dis[u]+ed[i].co; aa[v]=min(aa[u],ed[i].va); pre[v]=i; if (!vi[v]) vi[que[tail=tail%len+1]=v]=true; } }if (dis[tt]==inf) return false; flow+=aa[tt];cost+=aa[tt]*dis[tt]; for (i=tt;i!=ss;i=ed[pre[i]].u){ ed[pre[i]].va-=aa[tt]; ed[pre[i]^1].va+=aa[tt]; }return true;} void dp(int u,int ff){ int i,j,k,v,v1,v2,son=0; for (i=point[u];i;i=next[i]){ if ((v=en[i])==ff||fb[i]) continue; dp(v,u);++son; }for (i=1;i<=n;++i){ if (th[i]!=th[u]) continue;++mn; ci[ci[0]=1]=ss;ci[++ci[0]]=tt; gi[ss]=gi[tt]=mn;tot=1; for (j=point[u];j;j=next[j]){ if ((v1=en[j])==ff||fb[j]) continue; for (k=point[i];k;k=next[k]){ if (fb[k]) continue; v2=en[k]; if (th[v1]!=th[v2]) continue; add1(v1,v2+n,1,fi[v1][v2]); }add1(ss,v1,1,0); }for (k=point[i];k;k=next[k]) if (!fb[k]) add1(en[k]+n,tt,1,0); flow=cost=0;while(spfa()); if (flow>=son) fi[u][i]=cost+(ai[u]!=bi[i]); for (j=1;j<=ci[0];++j) po1[ci[j]]=0; } } int main(){ int i,j,u,v,ans;scanf("%d",&n); for (tot=0,i=1;i<n;++i){scanf("%d%d",&u,&v);add(u,v);} for (i=1;i<=n;++i){rv[i]=(UL)rand();scanf("%d",&ai[i]);} for (i=1;i<=n;++i) scanf("%d",&bi[i]); mn=n;getrt(1,0); if (zh[0]==1) rt=zh[1]; else{ rt=(++n);add(rt,zh[1]);add(rt,zh[2]); for (i=point[zh[1]];i;i=next[i]) if (en[i]==zh[2]) fb[i]=true; for (i=point[zh[2]];i;i=next[i]) if (en[i]==zh[1]) fb[i]=true; ai[rt]=bi[rt]=0; }ss=0;tt=(n<<1)+1; memset(fi,127/3,sizeof(fi)); geth(rt,0);mn=0;dp(rt,0); for (ans=inf,i=1;i<=n;++i) ans=min(ans,fi[rt][i]); printf("%d\n",ans); }
bzoj1570 Blue Mary的旅行
题目大意：给定n个城市，m条有向边，t个人要从1到n，边i每天能通过的人数为bi，问最后一个人到n的天数。
思路：对每个点拆n+t（答案上界）个点，从这一天的x到下一天的y连边流量bi费用1，源点到第一天1号点连流量t，每天从n连到汇点流量t，从第i天1号点向第i+1天1号点连边流量t费用1。最后一次增广的费用就是答案了。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define up 105 #define N 5555 #define M 1000000 #define len 1000000 #define inf 2100000000 using namespace std; struct use{int u,v,va,co;}ed[M]; int point[N]={0},next[M],dis[N],pre[N],ai[N],ans,ss,tt,tot,id[up][up],que[len+1]; bool vi[N]={false}; void add(int u,int v,int va,int co){ next[++tot]=point[u];point[u]=tot;ed[tot]=(use){u,v,va,co}; next[++tot]=point[v];point[v]=tot;ed[tot]=(use){v,u,0,-co};} bool spfa(){ int i,u,v,head=0,tail; memset(dis,127,sizeof(dis)); vi[que[tail=1]=ss]=true; ai[ss]=inf;dis[ss]=0; while(head!=tail){ vi[u=que[head=head%len+1]]=false; for (i=point[u];i;i=next[i]) if (ed[i].va&&dis[v=ed[i].v]>dis[u]+ed[i].co){ dis[v]=dis[u]+ed[i].co; pre[v]=i;ai[v]=min(ai[u],ed[i].va); if (!vi[v]) vi[que[tail=tail%len+1]=v]=true; } }if (dis[tt]==dis[N-1]) return false; ans=dis[tt]; for (i=tt;i!=ss;i=ed[pre[i]].u){ ed[pre[i]].va-=ai[tt]; ed[pre[i]^1].va+=ai[tt]; }return true;} int main(){ int n,m,i,j,u,v,vv,t; scanf("%d%d%d",&n,&m,&t); for (tot=0,i=1;i<=n;++i) for (j=n+t;j;--j) id[i][j]=++tot; ss=0;tt=tot+1;tot=1; add(ss,id[1][1],t,0); for (i=n+t;i;--i){ add(id[n][i],tt,t,0); if (i>1) add(id[1][i-1],id[1][i],t,1); }for (i=1;i<=m;++i){ scanf("%d%d%d",&u,&v,&vv); for (j=n+t-1;j;--j) add(id[u][j],id[v][j+1],vv,1); }while(spfa()); printf("%d\n",ans); }
（一开始想对每个点拆t天和自己的点，对于x->y的边从x到y的第i天连边费用i，这样跑出来的不能保证对于i天时这趟线路只跑bi。）
bzoj2668 交换棋子
题目大意：给一个有黑白棋子的棋盘，每次可以交换相邻格子（周围八个格子），每个格子有交换上界，问能否从始态到终态。
思路：考虑把黑棋换到终态的黑棋，一条交换路径中第一条和最后一条是1次，中间的是2次，一个点的限制是c/2，如果是原图的就+1再/2，如果是终图的就+1再/2，其他的能交换的连边1，1，从源点到原图黑点连边1，0，从终图黑点向汇点连边1，0。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define uu 25 #define N 805 #define M 1000005 #define len 1000000 #define inf 2100000000 using namespace std; struct use{int u,v,va,co;}ed[M]; int point[N]={0},next[M],tot,ss,tt,dis[N],pre[N],ai[N],que[len|1], fl=0,co=0,map[2][uu][uu],id[2][uu][uu], dx[8]={-1,-1,-1,0,0,1,1,1},dy[8]={-1,0,1,-1,1,-1,0,1}; bool vi[N]={false}; int in(){ char ch=getchar(); while(ch<'0'||ch>'9') ch=getchar(); return ch-'0';} void add(int u,int v,int vv,int cc){ next[++tot]=point[u];point[u]=tot;ed[tot]=(use){u,v,vv,cc}; next[++tot]=point[v];point[v]=tot;ed[tot]=(use){v,u,0,-cc};} bool spfa(){ int i,u,v,head=0,tail; memset(dis,127,sizeof(dis));dis[ss]=0; vi[que[tail=1]=ss]=true;ai[ss]=inf; while(head!=tail){ vi[u=que[head=head%len+1]]=false; for (i=point[u];i;i=next[i]) if (ed[i].va&&dis[v=ed[i].v]>dis[u]+ed[i].co){ dis[v]=dis[u]+ed[i].co;pre[v]=i; ai[v]=min(ai[u],ed[i].va); if (!vi[v]) vi[que[tail=tail%len+1]=v]=true; } }if (dis[tt]==dis[N-1]) return false; fl+=ai[tt];co+=ai[tt]*dis[tt]; for (i=tt;i!=ss;i=ed[pre[i]].u){ ed[pre[i]].va-=ai[tt]; ed[pre[i]^1].va+=ai[tt]; }return true;} int main(){ int i,j,k,n,m,x,y,c1=0,c2=0;tot=0, scanf("%d%d",&n,&m); for (i=1;i<=n;++i) for (j=1;j<=m;++j){ map[0][i][j]=in(); c1+=map[0][i][j]; id[0][i][j]=++tot; id[1][i][j]=++tot; }ss=0;tt=tot+1; for (i=1;i<=n;++i) for (j=1;j<=m;++j) c2+=(map[1][i][j]=in()); for (tot=i=1;i<=n;++i) for (j=1;j<=m;++j){ x=in()+map[0][i][j]+map[1][i][j]; if (map[0][i][j]) add(ss,id[0][i][j],1,0); add(id[0][i][j],id[1][i][j],x>>1,0); if (map[1][i][j]) add(id[1][i][j],tt,1,0); for (k=0;k<8;++k){ x=i+dx[k];y=j+dy[k]; if (x<=0||x>n||y<=0||y>m) continue; add(id[1][i][j],id[0][x][y],inf,1); } } while(spfa()); if (fl==c1&&c1==c2) printf("%d\n",co); else printf("-1\n"); }
dinic
bzoj3532 lis
题目大意：给定一个数组，有三个参数（权值ai，改动代价bi，优先级ci），删掉一些数，使原数列最长上升子序列长度至少-1，求最小改动代价的前提下优先级升序的字典序最小的方案。
思路：求最小代价是比较裸的最小割，但是方案就比较复杂了。考虑如果一个数是最小割上的边（流量为0且不能从这条边的起点向终点找到增广路）删掉了（从优先级小的向大的贪心），就需要把这个数拆的点之间的边的流量退掉，这里有一种退流算法：从终点向这条边的终点和这条边的起点向起点做两遍最大流，然后把这条边和兄弟边的权值赋为0就可以了。
（写的isaptle了，但是dinic就a了。。。）
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<ctime> #define maxm 1405 #define maxx 1000000 #define inf 2000000005 #define LL long long using namespace std; struct use{int st,en;LL va;}ed[maxx]; struct uu{ int cc,po; bool operator<(const uu&x)const{return cc<x.cc;} }ci[maxm]; int tot,point[maxm],next[maxx],ai[maxm],fi[maxm],xi[maxm],cur[maxm],n,que[maxm], dis[maxm],ansi[maxm]; LL bi[maxm]; int idx(int x,int y){return x*2-1+y;} void add(int u,int v,LL vv){ next[++tot]=point[u];point[u]=tot;ed[tot]=(use){u,v,vv}; next[++tot]=point[v];point[v]=tot;ed[tot]=(use){v,u,0LL}; } bool bfs(int st,int en){ int u,i,v,head=0,tail; memset(dis,-60,sizeof(dis)); for (i=2*n+1;i>=0;--i) cur[i]=point[i]; dis[que[tail=1]=en]=0; while(head!=tail){ u=que[++head]; for (i=point[u];i;i=next[i]) if (ed[i^1].va && dis[v=ed[i].en]<0) dis[que[++tail]=v]=dis[u]+1; }return dis[st]>=0; } LL dfs(int u,int en,LL mf){ if (u==en) return mf; int i,j,v;LL fl,cnt=0LL; for (i=cur[u];i&&mf;i=next[i]){ cur[u]=i;v=ed[i].en; if (ed[i].va&&dis[v]+1==dis[u]&&(fl=dfs(v,en,min(mf,ed[i].va)))){ ed[i].va-=fl;ed[i^1].va+=fl; mf-=fl;cnt+=fl; } }return cnt; } LL dinic(int st,int en){ LL ans=0LL; while(bfs(st,en)) ans+=dfs(st,en,inf); return ans; } int main(){ int i,j,t,lm,st,en;scanf("%d",&t); while(t--){ scanf("%d",&n);st=lm=0;en=2*n+1; memset(point,0,sizeof(point)); for (tot=i=1;i<=n;++i){ scanf("%d",&ai[i]);fi[i]=0; for (j=1;j<i;++j) if (ai[j]<ai[i]&&fi[j]>fi[i]) fi[i]=fi[j]; if ((++fi[i])==1) add(st,idx(i,0),inf); else for (j=1;j<i;++j) if (ai[j]<ai[i]&&fi[j]+1==fi[i]) add(idx(j,1),idx(i,0),inf); lm=max(lm,fi[i]); }for (i=1;i<=n;++i){ scanf("%I64d",&bi[i]);xi[i]=tot+1; add(idx(i,0),idx(i,1),bi[i]); }for (i=1;i<=n;++i){ scanf("%d",&ci[i].cc);ci[i].po=i; if (fi[i]==lm) add(idx(i,1),en,inf); }printf("%I64d ",dinic(st,en)); sort(ci+1,ci+n+1);ansi[0]=0; for (i=1;i<=n;++i){ lm=xi[j=ci[i].po]; if (!ed[lm].va && !bfs(idx(j,0),idx(j,1))){ ansi[++ansi[0]]=j; dinic(en,idx(j,1));dinic(idx(j,0),st); ed[lm].va=ed[lm^1].va=0; } }printf("%d\n",ansi[0]); sort(ansi+1,ansi+ansi[0]+1); for (i=1;i<ansi[0];++i) printf("%d ",ansi[i]); if (ansi[0]) printf("%d\n",ansi[ansi[0]]); } }
