Light OJ 1199 - Partitioning Game (博弈sg函数)

D - Partitioning Game

Time Limit:4000MS     Memory Limit:32768KB     64bit IO Format:%lld & %llu

Submit Status

Description

Alice and Bob are playing a strange game. The rules of the game are:

1. Initially there are n piles.
2. A pile is formed by some cells.
3. Alice starts the game and they alternate turns.
4. In each tern a player can pick any pile and divide it into two unequal piles.
5. If a player cannot do so, he/she loses the game.

Now you are given the number of cells in each of the piles, you have to find the winner of the game if both of them play optimally.

Input

Input starts with an integer T (≤ 1000), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 100). The next line contains n integers, where the i^th integer denotes the number of cells in the i^th pile. You can assume that the number of cells in each pile is between 1 and 10000.

Output

For each case, print the case number and 'Alice' or 'Bob' depending on the winner of the game.

Sample Input

3

1

4

3

1 2 3

1

7

Sample Output

Case 1: Bob

Case 2: Alice

Case 3: Bob

题意：有n堆石子(1<=n<=100)，每一堆分别有xi个石子(1<=xi<=10000)，
　　　一次操作可以使一堆石子变成两堆数目不相等的石子，
　　　最后不能操作的算输，问先手胜还是后手胜。
思路：n堆石子相互独立，所以可以应用SG定理，只需要算出一堆石子的SG函数。
　　　一堆石子（假设有x个）的后继状态可以枚举出来，分别是{1,x-1},{2,x-2},...,{(x-1)/2,x-(x-1)/2}，
　　　一堆石子分成的两堆石子又相互独立，再次应用SG定理。

　　　所以SG(x) = mex{ SG(1)^SG(x-1), SG(2)^SG(x-2),..., SG((x-1)/2)^SG(x-(x-1)/2) }，

　　　最后的答案是SG(x1)^SG(x2)^...^SG(xn)

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int sg[10005]= {0};
bool vis[10005];
int t,cas=1;
void get()
{
    memset(sg,0,sizeof(sg));
    for(int i=1; i<=10000; i++) //i=0相当于空石子堆 不符合题意
    {
        memset(vis,0,sizeof(vis));
        for(int j=1; j+j<i; j++) //j=0相当于没分 j=i/2 相当于分成相等的两堆 这两种情况都是不可以的
            vis[sg[j]^sg[i-j]]=1;
        for(int x=0; x<=10000; x++)
            if(!vis[x])
                {
                    sg[i]=x;
                    break; //一定别忘了break
                }
    }
}
void pra()
{
    printf("Case %d: Alice\n",cas++);
}
void prb()
{
    printf("Case %d: Bob\n",cas++);
}
int main()
{
    get();
    cin>>t;
    while(t--)
    {
        int n,data,ans=0;
        cin>>n;
        for(int i=0; i<n; i++)
        {
            cin>>data;
            ans^=sg[data]; //是sg[data]不是data 对于B来说每个都是0最好了
        }
        if(ans)
            pra();
        else
            prb();
    }
    return 0;
}

 

 对sg函数的理解：

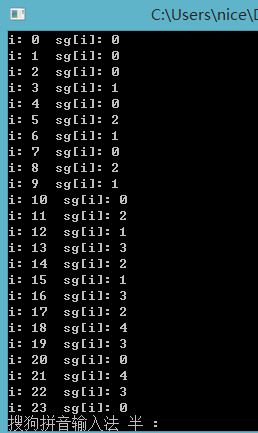
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int sg[10005];
int hash[10005];
void getsg()
{
    memset(sg,0,sizeof(sg));
    for(int i=1;i<=10000;i++)
    {
        memset(hash,0,sizeof(hash));
        for(int j=1;j+j<i;j++) //不相等的两堆
        //注意是sg[j]不是sg[i]
            hash[sg[j]^sg[i-j]]=1; //sg[j]^sg[i-j] 是i的后继  i是从小到大跑的 所以不需要搜索直接用即可
            //小的数是大的数的后继 sg[1]^sg[4]=0,sg[2]^sg[3]=1是sg[5]=2的后继
        for(int x=0;x<=10000;x++)//不是0的就是必胜点
            //只要在上面的sg里能异或出来一个等于0的 就是后继里有一个是等于0的 这个点就是必胜点
            //多个点异或和以前的思想一样 看成n个有向图
            //i小的时候可以这么看
            //根据题意 不能分的点比如1或者分了以后还能分一次的点比如4 就是必败点 sg值为0
            //i的异或值就是i 分成两个数看他俩的异或值是多少 如果分成的两个数的异或值中存在0说明该点是胜的
            if(!hash[x])
            {
                sg[i]=x;
                break;
            }
    }
}
int main()
{
    getsg();
    for(int i=0;i<50;i++)
    cout<<"i: "<<i<<"  sg[i]: "<<sg[i]<<endl;
    /*int t,cas=1;
    cin>>t;
    while(t--)
    {
        int n,data,ans=0;
        cin>>n;
        for(int i=0;i<n;i++)
        {
            cin>>data;
            ans^=sg[data];
        }
        if(ans)
            printf("Case %d: Alice\n",cas++);
        else
            printf("Case %d: Bob\n",cas++);
    }*/
    return 0;
}