最小生成树算法

最小生成树是指在一个图中，由连接所有顶点的边构成的权值之和最小的树，求最小生成树的算法主要有Prim算法及Kruskal算法，此处介绍Prim算法的基本原理。

Prim算法是一种贪心算法，不过可以证明，此算法得到的必定是全局最优解。Prim算法的基本思路如下：

1. 将图中的所有顶点分为两个集合，Known及Unknown，初始时任意选择一个顶点放置在Known中，其余顶点位于Unknown中，算法的目标是将Unknown中的所有顶点移至Known中；
2. 选择一条边，这条边连接的两个顶点一个位于Known中，另一个位于Unknown中，且这条边的权值是所有满足条件的边中最小的；
3. 将这条边添加到最小生成树中，并将其连接的那个位于Unknown集合中的顶点移至Known中；
4. 重复以上两步，直至Unknown集合为空；

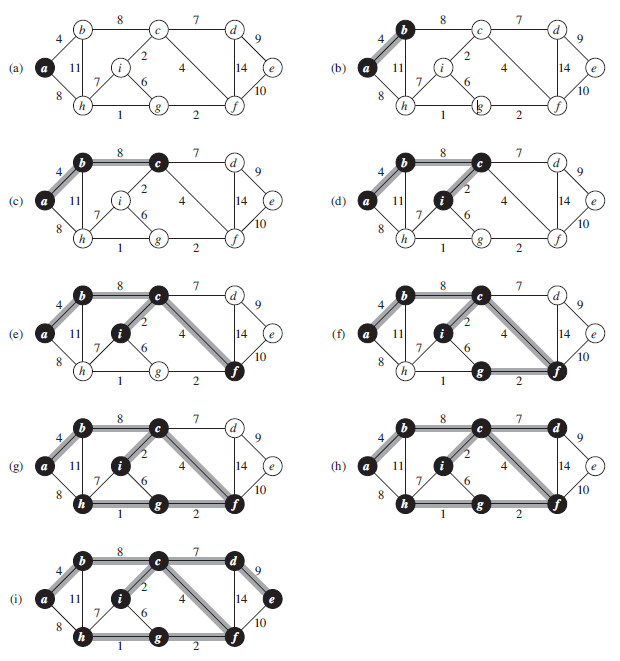
算法图示：

算法图示

Prim算法的过程与Dijkstra算法很相像，故二者的程序结构也很类似。

在使用邻接表及二叉堆实现时，Prim算法的时间复杂度是 $O(|E|log|V|)$，需要注意的是，无论对于稀疏图还是稠密图，这都是一个最优的算法复杂度。Kruskal算法的复杂度是 $O(|E|log|E|)$，对于所有连通图来说都有 $|E|>=|V|-1$，所以可以得出结论，Prim算法在时间复杂度上无论是对于稀疏图还是稠密图来说都是最优的，优于Kruskal算法。不过其最大缺点就是在使用二叉堆时空间复杂度会极大，对于超稠密图就很不合适了。具体定量比较可参考：

Prim、Kruskal、Prim+Heap算法效率实测

算法的实现代码有空再补上吧……

or 参考： 最小生成树的常用算法模板