二重积分的计算:交换积分次序
为什么要改积分次序:
- 题面要求(交换积分次序)
- 次序不对,无法计算
- 积分法不对
- ?
顺口溜:
-
后积先定线,限内穿条线,先交下线写,后交上线见
-
先积 \(x\) ,画横线(平行于 \(x\) 轴)
先积 \(y\) ,画竖线(平行于 \(y\) 轴)
以下几种被积函数在交换次序后可以优化计算
-
\(x^{2n}e^{\plusmn x^2} dx\)
-
\(e^{\frac{1}{x}}dx\)
-
\(sin(\frac{1}{x}) dx\)
\(cos(\frac{1}{x}) dx\)
简单举例
函数图来源:https://mathinsight.org/double_integral_change_order_integration_examples
\[\int_{0}^{1} \int_{1}^{e^{y}} f(x, y) d x d y
\]
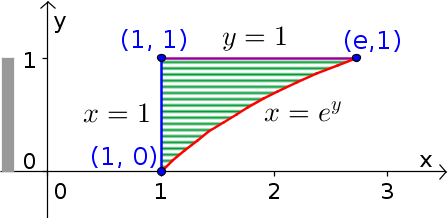
交换之后,先积 y 划竖线,上减下,则有:
\[\int_{1}^{e}\left\{\int_{\ln x}^{1} f(x, y) d y\right\} d x
\]



