Codeforces Round #619 (Div. 2) A-D

比赛链接：Here

1301A. Three Strings

题意：

给三个相同长的字符串 $a, b, c$ ，对于每个位置 $i$ ，你必须做一次操作：交换 $a_{i}$ 和 $c_{i}$ ，或者交换 $b_{i}$ 和 $c_{i}$ 。问你交换完之后 $a$ 和 $b$ 能否一样。

因为每个位置必须交换，所以每个位置只要 $a_{i} = c_{i}$ 或者 $b_{i} = c_{i}$ 即可

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int _; for (cin >> _; _--;) {
        string a, b, c;
        cin >> a >> b >> c;
        bool f = 1;
        for (int i = 0; f and i < a.size(); ++i) {
            if (a[i] == c[i] || b[i] == c[i]) continue;
            f = 0;
        }
        cout << (f ? "YES\n" : "NO\n");
    }
}

1301B. Motarack's Birthday

题意：

给一个长为 $n$ 的整数数组，其中有一些数消失了，用 $- 1$ 代替，其他数大于等于 $0$ ，然后叫你找一个非负数 $k$ ，使得用 $k$ 替代所有 $- 1$ 后，相邻元素的差值的最大值，这个值要最小。

思路：

差值最大值无非就是，原来就有的数之间的相邻差值最大值，和替换后k与原来就有的数的差值的最大值里求一个 $max$ 。前者可以直接求的，后者当 $k$ 取到 $(m_{i} + m x) / 2$ 时取到最小。 $m_{i}$ 为与 $k - 1$ 邻的原来有的数的最小值， $m x$ 为最大值。

const int N = 1e5 + 10;
ll a[N];
int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int _; for (cin >> _; _--;) {
        int n; cin >> n;
        for (int i = 0; i < n; ++i) cin >> a[i];
        ll base = 0;
        vector<ll>v;
        for (int i = 0; i < n - 1; ++i) {
            if (a[i] == -1 and a[i + 1] != -1) v.push_back(a[i + 1]);
            else if (a[i] != -1 and a[i + 1] == -1) v.push_back(a[i]);
            else if (a[i] != -1 and a[i] != -1) base = max(base, abs(a[i] - a[i + 1]));
        }
        if (v.empty()) {cout << "0 0\n"; continue;}
        sort(v.begin(), v.end());
        int k = (v.back() + *v.begin()) / 2;
        cout << max(max(v.back() - k, k - v[0]), base) << " " << k << "\n";
    }
}

1301C. Ayoub's function

题意：

函数 $f (s)$ 代表， $01$ 字符串 $s$ 中包含至少一个 $1$ 的子串的数量。问你所有长度为 $n$ ，其中有 $m$ 个 $1$ 的 $01$ 字符串中。使得 $f (s)$ 的值最大为多少。

做法：

至少包含一个 $1$ 的子串的数量 $=$ 所有子串的数量 $-$ 只包含 $0$ 的子串的数量。

所以要使得 $f (s)$ 越大，只包含 $0$ 的子串的数量要越小越好，于是 $01$ 字符串中每一段的连续的 $0$ 的个数应尽可能一样。 $m$ 个 $1$ ，有 $n - m$ 个 $0$ ，被分成 $m + 1$ 段，长度为 $(n - m) / (m + 1) + 1$ 的连续 $0$ 的段数为 $(n - m)$ ，长度为 $(n - m) / (m + 1)$ 的连续 $0$ 的段数为 $m + 1 - (n - m)$ 。再计算一下可得答案。

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int _; for (cin >> _; _--;) {
        ll n, m; cin >> n >> m;
        ll ans = n * (n + 1) / 2;
        ll num = (n - m) / (m + 1);
        ll r = (n - m) % (m + 1);
        cout << (ans - r * (num + 1) * (num + 2) / 2 - (m + 1 - r) * num * (num + 1) / 2) << "\n";
    }
}

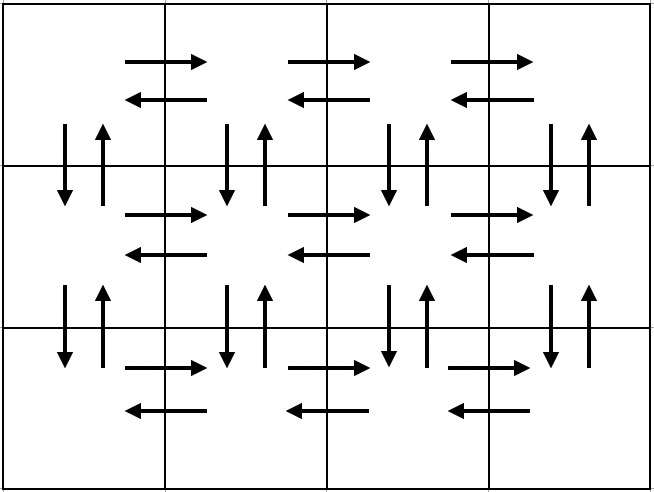
1301D. Time to Run

题意：

$n * m$ 的网格，相邻网格间有两条道路（不同方向）。问你能否不重复的走 $k$ 条路，可以的话输出路径。按题目要求。

img

思路：

真就直接走完咯，先左右走，到最后一行只往右，到右下角之后上下走，ok，然后题目要求 $k$ ，边走边减，到 $0$ 为止即可。如果全部都走过了 $k$ 还有剩就输出 NO.

int n, m, k;
vector<pair<int, string>>v, ans;
int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    cin >> n >> m >> k;
    for (int i = 0; i < n - 1; ++i) {
        if (m != 1) {
            v.push_back({m - 1, "R"});
            v.push_back({m - 1, "L"});
        }
        v.push_back({1, "D"});
    }
    if (m != 1) v.push_back({m - 1, "R"});
    for (int i = 0; i < m - 1; ++i) {
        if (n != 1) {
            v.push_back({n - 1, "U"});
            v.push_back({n - 1, "D"});
        }
        v.push_back({1, "L"});
    }
    if (n != 1) v.push_back({n - 1, "U"});
    for (int i = 0; i < v.size(); ++i) {
        if (k >= v[i].first) {
            k -= v[i].first;
            ans.push_back(v[i]);
        } else if (k != 0) {
            ans.push_back({k, v[i].second});
            k = 0;
        }
    }
    if (k > 0) cout << "NO\n";
    else {
        cout << "YES\n";
        cout << ans.size() << "\n";
        for (auto p : ans) cout << p.first << " " << p.second << "\n";
    }
}