【动态规划】树形DP完全详解！

蒟蒻大佬时隔三个月更新了！！拍手拍手

而且是更新了几篇关于DP的文章（RioTian狂喜）

现在赶紧复习一波树形DP....

树形DP基础：Here，CF上部分树形DP练习题：Here

\[QAQ \]

在学习树形DP之前，我们先要搞清楚一个问题，什么是树？根据图论课上学到的知识我们知道，连通的无圈图称为树。而树我们可以把它近似第看成一个分形结构，这是说我们的树其实是可以递归定义的，树的每个子树也是一颗完整的树，而这种结构就天然地适合递归。

具体来说，在树形动态规划当中，我们一般先算子树再进行合并，在实现上与树的后序遍历相似，都是先遍历子树，遍历完之后将子树的值传给父亲。简单来说我们动态规划的过程大概就是先递归访问所有子树，再在根上合并。

了解了树形动态规划的基本思想后，做一些经典的树形DP题型

【经典例题】

【子树大小】

Description

给你一棵有 $n$ 个点的树（$1$ 号点为根节点），求以 $i$ 为根的子树的大小。


这道题作为我们树形动态规划的引例，当然是非常简单的，只要跑一遍 \(DFS\) 即可求出。

具体细节：

  • 设 \(f_i\) 以 \(i\) 为根的子树大小，则 \(f[i] = \sum f[k] + 1\) ，其中 \(k\) 为 \(i\) 子节点。

    如果写成伪码，大概长这个样子

void dfs(u){
	if (u 是叶子) f[u] = 1 return
    for (v 是 u 的儿子){
        dfs(v)
        f[u] += f[v]
    }
    f[u] += 1 // 本身
}

这就是最简单的树形DP了，有没有感受到先遍历子树，遍历完之后将子树的值传给父亲这样的动态规划过程呢？

【树的平衡点】

Description

给你一个有 $n$ 个点的树，求树的平衡点和删除平衡点后最大子树的节点数。所谓平衡点，指的是树中的一个点，删掉该点，使剩下的若干个连通块中，最大的连通块的块大小最少。


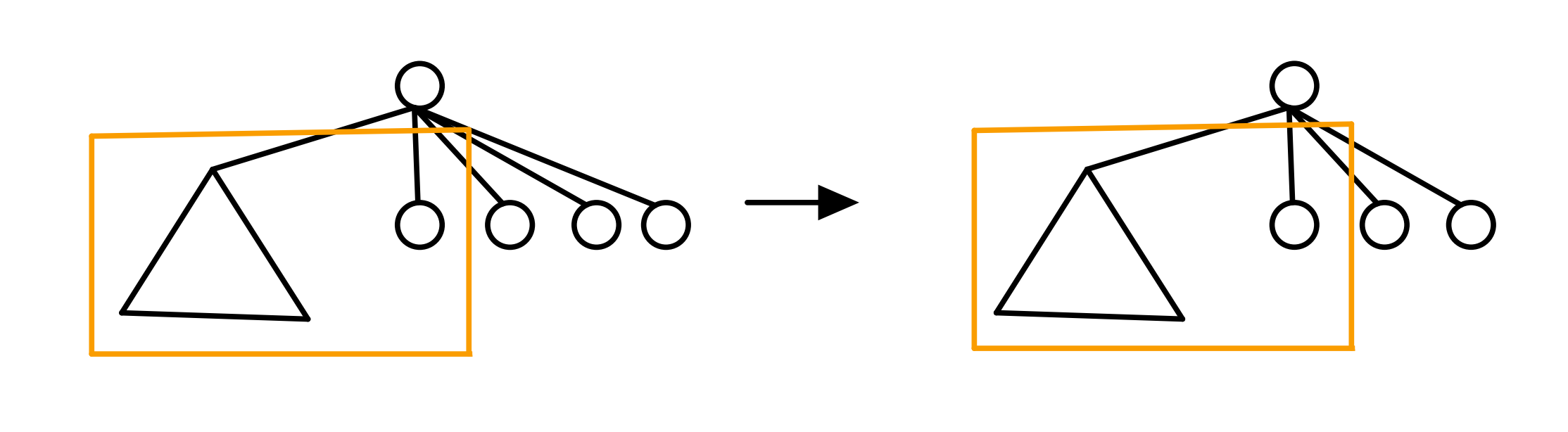
要解决这个问题，我们首先还是先确定状态，现在的问题还很简单，一般就是题目问什么我们就设什么，所以我们先设 \(F[i]\)​​ 为删除 \(i\)​​ 号点后最大连通块的块大小。然后我们沿用上一题的设 \(f[i]\)​​ 为以 \(i\)​​ 为根的子树大小，那么很简单就有 \(F[i]=max(n−f[i],max(f[k]))\)​​，其中 \(k\)​​ 是 \(i\)​ 的子节点。这是因为，删除 \(i\)​ 号点后，我们剩下的连通块要么是 \(i\) 的子树，要么是 \(i\)​ 的父亲所在的连通块。

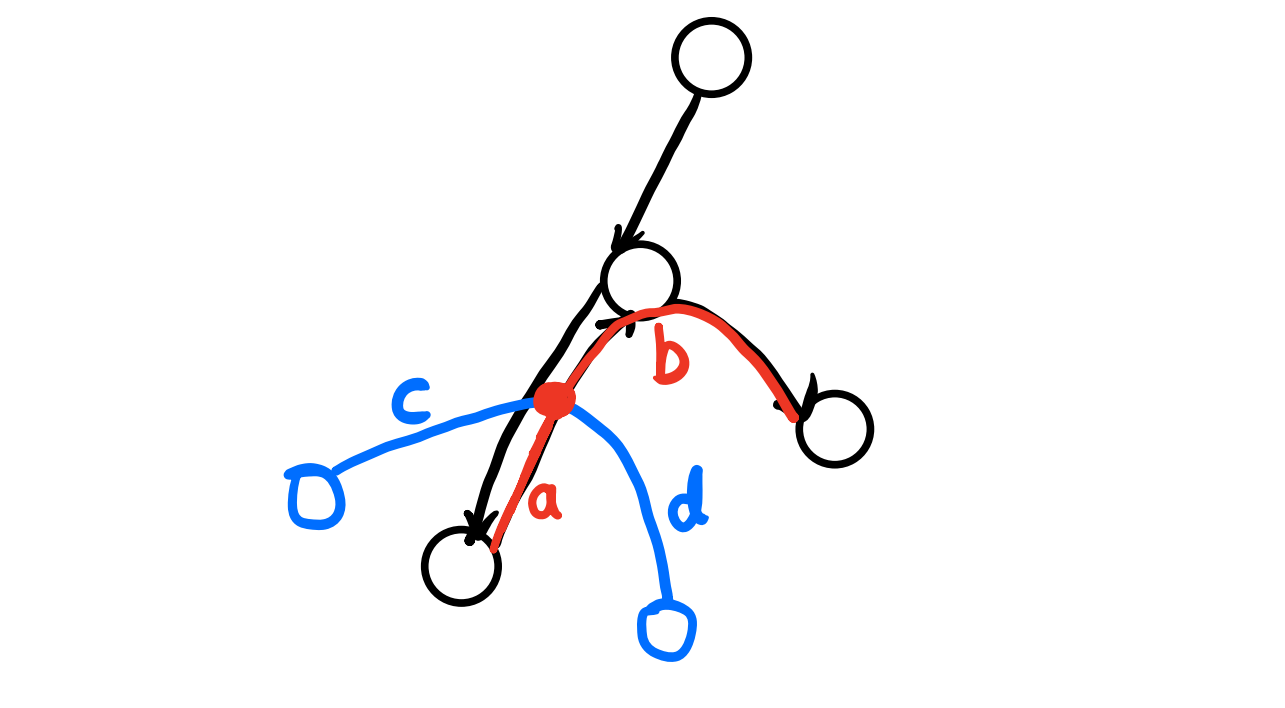
通俗的来讲，即删除某个节点后，它的儿子就成了独立的连通块，那么最大连通块就是 max(x 的所有儿子连通块最大的 size，n - f[x])

借用一下蒟蒻dalao的图

树的平衡点示意图

所以我们只需要先沿用第一题的方法先算出每个点的子树大小，再 \(DFS\) 一遍算出每个点的 \(F[i]\)​ ，其值最小的点就是我们树的平衡点啦。

【代码实现】

 vector<int>e[N];
int ans, idx, f[N];
void dfs(int u, int fa) {
    f[u] = 1;
    int mx = 0;
    for (int v : e[u]) {
        if (v == fa)continue;
        dfs(v, u);
        f[u] += f[v];
        mx = max(mx, f[v]);
    }
    mx = max(mx, n - f[u]);
    if (ans > mx) ans = mx, idx = u;
}

没有上司的舞会 （树的最大独立集）

Description

有 $n$ 名职员，编号为 $1\sim n$ ，他们的关系就像一棵以老板为根的树，父节点就是子节点的直接上司。每个职员有一个快乐指数，用整数 $H_i$ 给出，现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。在满足这个条件的前提下，主办方希望邀请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。


这个在 树形DP基础 里讲过了

我们把题意抽象一下，没有职员会和上司一同参会，也就是说在这棵树上不存在任何一条边使得连接的两个点都来参会，换句话说这道题其实要我们求的是 树的最大权值的独立集。

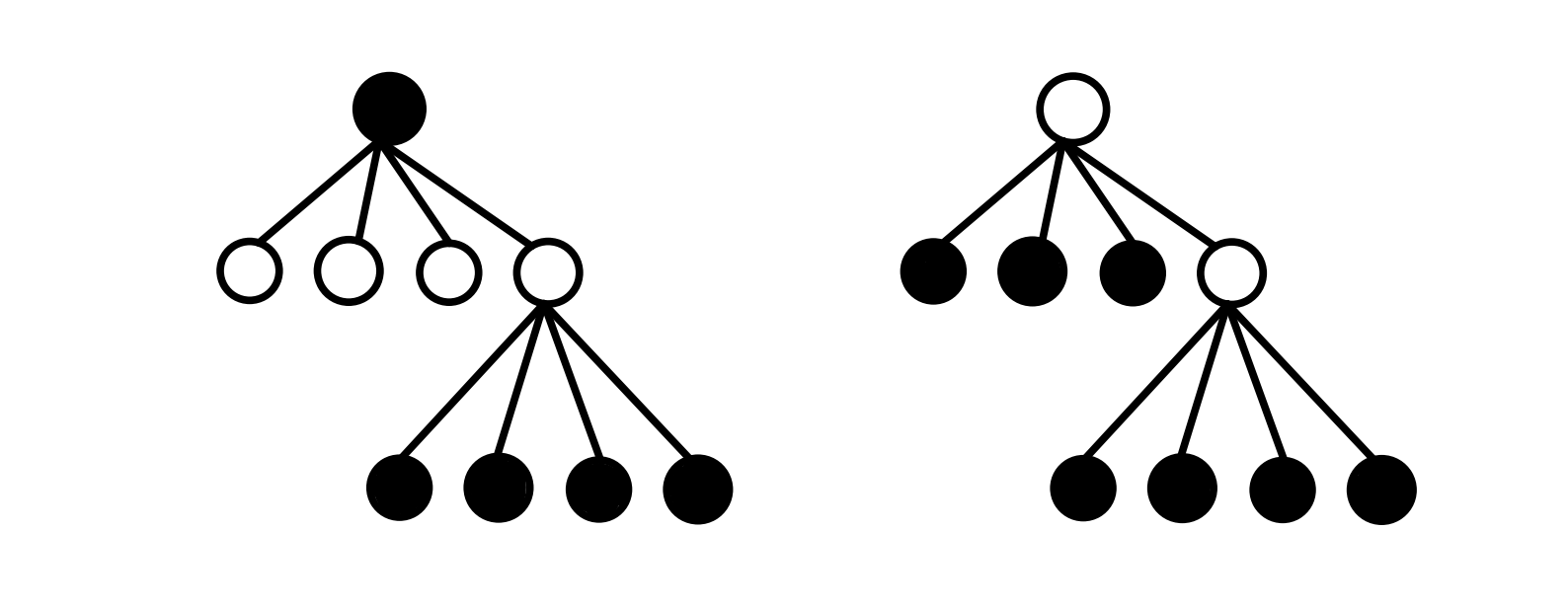
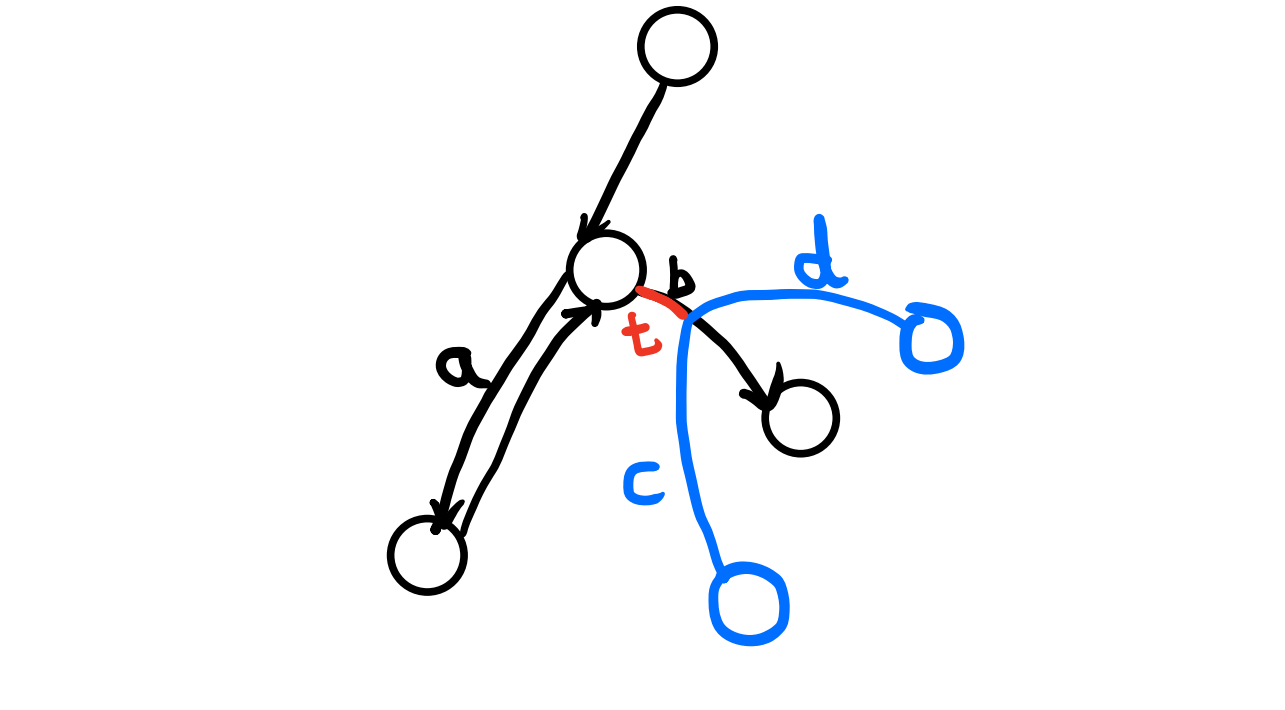
蒟蒻大佬在他的博客提到了——— 黑白染色，也就是在树上一层选一层不选这样的贪心。

但其实很容易证明简单的黑白染色是不对的，如下图所示，左边是黑白染色的结果，右边是正解的结果。其中黑点表示要来参加的人，白点表示不来参加的人，在这个例子中我们默认每个人的快乐指数都是一样的。

树的最大独立集示意图

所以我们只好老老实实地去确定状态一步一步来。我们发现 \(i\)​ 号点选或者不选其实是会影响子树的结果的，我们要在状态中将这一层影响交代清楚。所以我们用 \(f[i][0]\)​ 表示不选 \(i\)​ 点去参加舞会时 \(i\)​ 点及其子树所能选的最大的快乐指数； \(f[i][1]\) 表示选 \(i\) 点去参加舞会时 \(i\) 点及其子树所能选的最大的快乐指数。然后我们考虑怎么转移，当不选 \(i\)​ 点去参加舞会时，它的儿子们可以参加也可以不参加，所以有如下的转移方程

转移方程：\(f[i][0] = \sum(max(f[k][0],f[k][1]))\)​​ ，其中 \(k\) 是 \(i\)​ 的儿子；

  • 当选 \(i\) 去参加舞会时，它的儿子不能参加，所以 \(f[i][0] = \sum f[k][0] + H_i\)

其中我们的边界条件就是当 \(i\) 是叶子时 \(f[i][0] = 0,f[i][1] = H_i\)

我们最后的答案就是 \(ans = max(f[root][0],f[root][1])\)

而如果转变为树的最大独立集就只要让我们的 $ H_i = 1$​ 对所有点成立就可以了。

【AC Code】

const int N = 1e4 + 10;
vector tr[N];
int f[N][2], v[N], Happy[N], n;
void dfs(int u) {
    f[u][0] = 0; f[u][1] = Happy[u];
    for (auto v : tr[u]) {
        dfs(v);
        f[u][0] += max(f[v][0], f[v][1]);
        f[u][1] += f[v][0];
    }
}
int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> Happy[i];
    for (int i = 1, x, y; i < n; ++i) {
        cin >> x >> y;
        v[x] = 1;// x has a father
        tr[y].push_back(x);
    }
    int root;
    for (int i = 1; i <= n; ++i)
        if (!v[i]) {root = i; break;}
    dfs(root);
    cout << max(f[root][0], f[root][1]) << "\n";
}

Strategic game （树的最小点覆盖）

Description

给你一个有 $n$ 个点的树，每两个点之间至多只有一条边。如果在一个结点上放一个士兵，那他能看守与之相连的边，问最少放多少个兵，才能把所有的边能看守住。


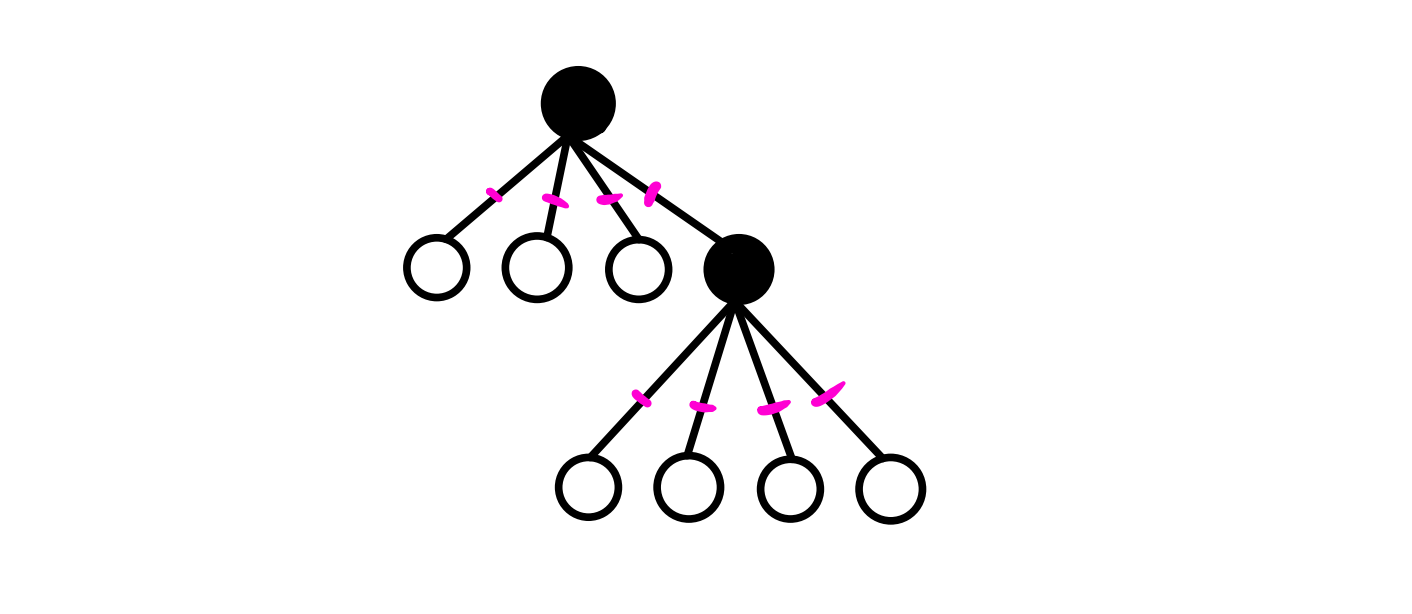
树的最小点覆盖,问题示意图

这道题和上一道题： 没有上司的舞会 （树的最大独立集） 挺像的，题目链接：Here

都是能够发现 \(i\) 号点选或不选是会影响子树的结果。但和上一题儿子父亲不能同时选不一样的是：儿子父亲不能同时选不一样。

那我们的状态就很明朗了，

  • 设 \(f[i][0]\) 为不在 \(i\) 号点上放士兵并且以 \(i\) 为根的每条边都被看住的最小士兵数；
  • 设 \(f[i][1]\) 为在 \(i\) 号点上放士兵并且以 \(i\)​ 为根的子树的每条边都被看住的最小士兵数。

接下来我们来考虑转移，

  • 当 \(i\)​ 点不放士兵时，它的儿子就必须都要放士兵，所以 \(f[i][0] = \sum f[k][1]\)​ ；

  • 当 \(i\) 点不放士兵时，它的儿子可以放士兵，也可以不放士兵，所以

    \(f[i][1] = 1 + \sum(min(f[k][0],f[k][1]))\)

我们最后的答案就是：\(ans = min(f[root][0],f[root][1])\)​

这就是树的最小点覆盖问题的解法。

vector<int>e[N];
int f[N][2];
bool st[N];
void dfs(int u) {
    st[u] = 1;
    f[u][0] = 0, f[u][1] = 1;
    for (int i = 0; i < e[u].size(); ++i) {
        int v = e[u][i];
        if (st[v]) continue;
        dfs(v);
        f[u][0] += f[v][1];
        f[u][1] += min(f[v][0], f[v][1]);
    }
}
int main() {
    int n, m, k, x;
    while (~scanf("%d", &n)) {
        for (int i = 1; i <= n; ++i) {
            scanf("%d:(%d)", &m, &k);
            while (k--) {
                scanf("%d", &x);
                e[m].push_back(x), e[x].push_back(m);
            }
        }
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            if (st[i]) continue;
            dfs(i);
            ans += min(f[i][0], f[i][1]);
        }
        printf("%d\n", ans);
        memset(st, 0, sizeof(st));
        for (int i = 0; i < N; ++i) e[i].clear();
    }
}

Cell Phone Network （树的最小支配集）

题目链接：Here

Description

给你一个有 $n$ 个点的树，每两个点之间至多只有一条边。如果在第 $i$ 个点部署信号塔，就可以让它和所有与它相连的点都收到信号。求最少部署多少个信号塔能让所有点都能收到信号。


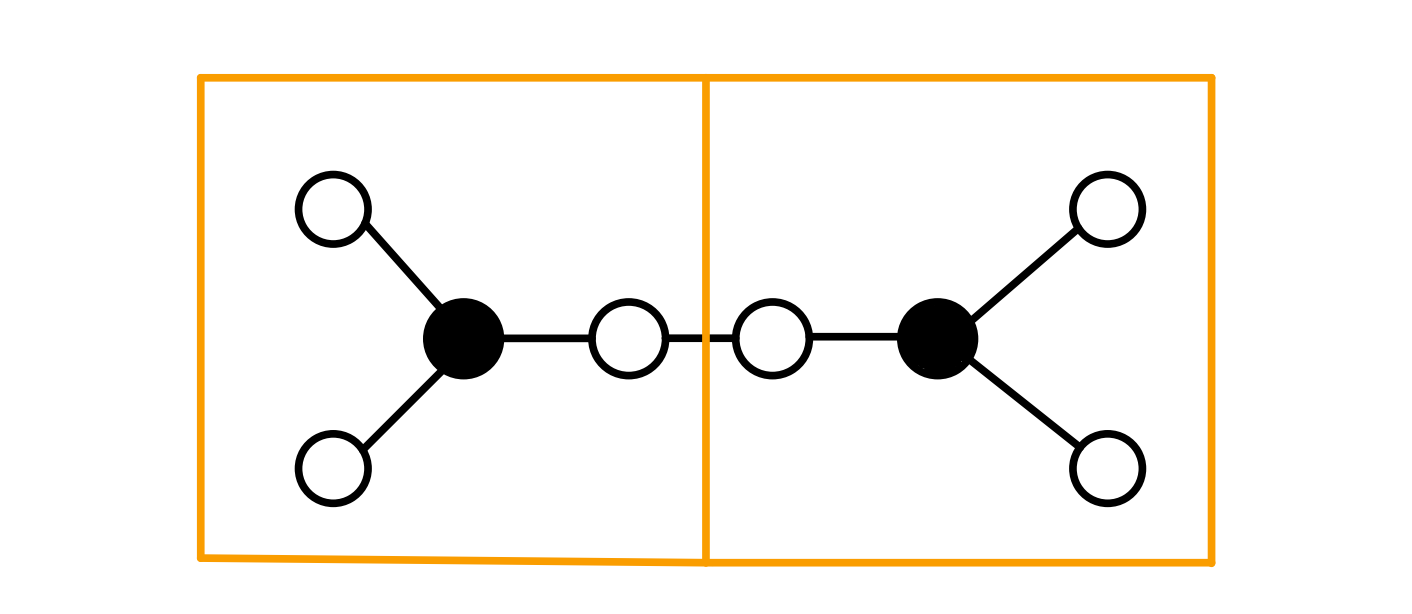
Cell Phone Network

这道题可以说是上两道题的升级版了，之前两道题一个点选或者不选，只会影响它的儿子选或者不选；但是在这道题当中，一个点选或者不选不仅会影响儿子还会影响父亲，所以在状态设计上会更加复杂一点点。

  • 设 \(f[i][0]\) 表示选点 \(i\)，且以 \(i\) 为根的子树每个点都被覆盖的最少信号塔部署数量；

  • 设 \(f[i][1]\) 表示不选点 \(i\)，并且 \(i\) 被儿子覆盖的最少信号塔部署数量；

  • 设 \(f[i][2]\) 为不选 \(i\)，但是 \(i\) 没被儿子覆盖，且以 \(i\)​ 为根的子树的其他点都被覆盖的最少信号塔部署数量，

    换句话说这时 \(i\) 的父亲一定要选来覆盖一下 \(i\)。

下面我们来看看如何进行转移。

  • 当我们选 \(i\) 点时，\(i\) 点的儿子可选可不选，并且可以已经被覆盖和未被覆盖，所以我们有

    \(f[i][0] = 1 + \sum(min(f[k][0],f[k][1],f[k][2]))\)

  • 当我们不选点 \(i\)，并且 \(i\) 未被覆盖的时候，它的儿子们都至少被覆盖或者不选，不能不选又不被覆盖，所以这个时候

    \(f[i][2] = \sum(f[k][1],f[k][0])\)

最难的情况是当我们不选点 \(i\)，并且 \(i\) 被覆盖的时候，这个情况是最复杂的情况，也就是这时 \(i\) 的所有儿子至少有一个被选，也就是至少有一个 \(f[k][0]\)，这时我们分情况讨论：

  1. 如果这时 \(i\) 存在一个儿子 \(k\) ，有 \(f[k][0] \le f[k][1]\) ，也就说选了它不会更劣，那么我们就选它，我们的答案回归 \(f[i][1] = \sum(f[k][1],f[k][0])\)
  2. 如果不存在这样一个儿子，也就是说对于所有儿子，选了都会变得更劣，那我们就要记录一下 \(minn = min(f[k][0] ,f[k][1])\) , 也就是选一个损失最小的来选，我们的答案就变成 \(f[i][1] = \sum(f[k][1],f[k][0]) + minn\) .

这题有点复杂我下面展示一下大致的参考代码：

void dfs(int x){
    v[x] = 1;
    f[x][0] = 1,f[x][1] = f[x][2] = 0;
    int tmp = inf;
    bool flag = 1;
    for(int i = 0;i < e[x].size();++i){
        int y = e[x][i];
        if(vis[y]) continue;
        dfs(y);
        f[x][2] += min(f[y][1],f[y][0]);
        f[x][0] += min(f[y][0],f[y][1],f[y][2]); // 重载min
        if(f[y][0] <= f[y][1]){
            flag = 0;
            f[x][1] += f[y][0];
        } else{
            f[x][1] += f[y][1];
            tmp = min(tmp,f[y][0] - f[y][1]);
        }
    }
    if(flag) f[x][1] += tmp;
}


// 简化思路的AC代码
const int N = 1e4 + 10, inf = 0x3f3f3f3f;
vector<int>e[N];
int ans;
bool vis[N];

void dfs(int u, int fa) {
    bool f = 0;
    for (int i = 0; i < e[u].size(); ++i) {
        int v = e[u][i];
        if (v == fa) continue;
        dfs(v, u); f |= vis[v];
    }
    if (!f && !vis[u] && !vis[fa])
        vis[fa] = 1, ans += 1;
}

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int n; cin >> n;
    for (int i = 1, x, y; i <= n; ++i) {
        cin >> x >> y;
        e[x].push_back(y);
        e[y].push_back(x);
    }
    dfs(1, 0);
    cout << ans;
}

到这里我们的最小支配集问题也得到了解决。

【二叉苹果树】树上背包问题

Description

有一棵二叉苹果树，如果数字有分叉，一定是分两叉，即没有只有一个儿子的节点。这棵树共 $N$ 个节点，标号 $1$ 至 $N$，树根编号一定为 。我们用一根树枝两端连接的节点编号描述一根树枝的位置，比如下图是一棵有四根树枝的苹果树。因为树枝太多了，需要剪枝。但是一些树枝上长有苹果，给定需要保留的树枝数量，求最多能留住多少苹果。


二叉苹果树-样例图

在刚学树形DP的时候遇到过，当时没能解决

题目链接：Here

首先这道题规定苹果是长在树枝上的，所以我们不妨设

  • \(a[i].l\) 表示连接 \(i\) 和其左儿子树枝上的苹果数量
  • \(a[i].r\)表示连接 \(i\)​ 和其右儿子树枝上的苹果数量

我们在这里由于最后要求在给定需要保留的树枝数量时最多能留住苹果的数量，所以我们不妨直接设 \(f[i][j]\) 表示以 \(i\) 为根的子树保留 \(j\) 个树枝时可以得到的最大的苹果数量。接下来我们就来考虑一下如何转移，我们的转移大致分为四种情况：

  • 首先是对于 \(i\)，它的左右子树都保留的情况，这时以 \(i\) 为根的子树保留 \(j\) 个树枝，我们再设左右子树分别保留 \(x\) 和 \(y\) 个树枝，那么我们有 \(x+y+2=j\)，所以我们就枚举 x，这时 \(y=j−2−x\)，所以这时

    \(f[i][j] = \max\limits_{x\in[0,j-2]}(f[l][x] + f[r][j - 2-x] + a[j].l + a[j].r)\)

    情况一

  • 接着是对于只保留左子树的情况，这时以 \(i\) 为根的子树保留 \(j\) 个树枝，所以左子树要保留 \(j−1\) 个树枝，所以这时 \(f[i][j]=f[l][j−1]+a[j].l\)

情况二

  • 其次是对于只保留右子树的情况，这时以 \(i\) 为根的子树保留 \(j\) 个树枝，所以右子树也要保留 \(j−1\) 个树枝，所以这时 \(f[i][j]=f[r][j−1]+a[j].r\)

情况三

  • 最后是左右子树都不保留的情况，这时 \(j=0\)，也就是 \(f[i][0]=0\) 。

这样分析完 \(4\) 种情况之后是不是感觉很简单呢？这时我们升级一下这道题，假如这棵树不是二叉树了，是多叉树的话我们要怎么办？我们假设这时是 \(k\) 叉树，这时最简单的做法就是枚举 \(k−1\) 叉的数量出来，剩下一个通过总和为 \(j\) 算出来进行转移。但是这样时间开销非常大，肯定是会 TLE 的。所以这时我们就要用到树上背包的思想。

我们先开一个虚构的左子树，如下图三角形，然后我们让第一个子树当作右子树和我们虚构的左子树合并，并将合并完的结果当成一个左子树再喝第二个子树合并，并将合并完的结果当作一个左子树和第三个子树合并……以此类推。而其中的合并就是我们上面二叉树枚举 \(x\) 的过程。也就是说在这个过程中我们不断将子树合并进入我们的左子树当中，强行当成二叉树进行操作。

具体写法的转移过程大概是这样的：

\(f[u][j] = max(f[u][k] + f[v][j - k - 1] + a[u][v])\) 其中 \(f[u][j]\) 表示的是以 i 为根的子树保留 j 个树枝时可以得到的最大的苹果数量，\(f[u][k]\) 就是我们的“左子树”保留 \(k\) 个树枝时可以得到的最大的苹果数量，\(v\) 是 \(u\) 的儿子，所以 \(f[v][j−k−1]\) 就是我们当前的“右儿子”保留 \(j−k−1\) 个树枝时可以得到的最大的苹果数量, \(a[u][k]\) 就是我们边上的苹果数量。

这其实就是一个树上背包的思想，希望同学们能够用心体会一下。

【树的直径】

另一篇关于树的直径的文章详细见这里：Here，练习：Here

Description

给你一个有 $n$ 个点的树，树上的每个点有一个权值。定义一棵树的子链大小为：这个子链上所有节点的权值和。求这棵树上最大子链的结点权值和。


原题链接：Here or Here

搜索基础好的同学可能已经看出来了，其实不用 DP ,两遍 DFS 也能解决问题。具体来说，我们从树上任意一个点以起点出发，找到一条最长的边然后以这条边的另一个顶点作为起点再 DFS 一遍找到的最长边就是我们树的直径。

树的直径示意图1

那一遍 DFS ，从一个点出发找一条第一长的找一条第二长的加起来行不行呢？那肯定是不行的，还是这个例子，我们选一个第一长的一个第二长的，就发现我们经过了一条公共边，这当然是不允许的。

树的直径示意图2

那这个两遍 DFS 为什么是对的呢，我们下面来感性证明一下。

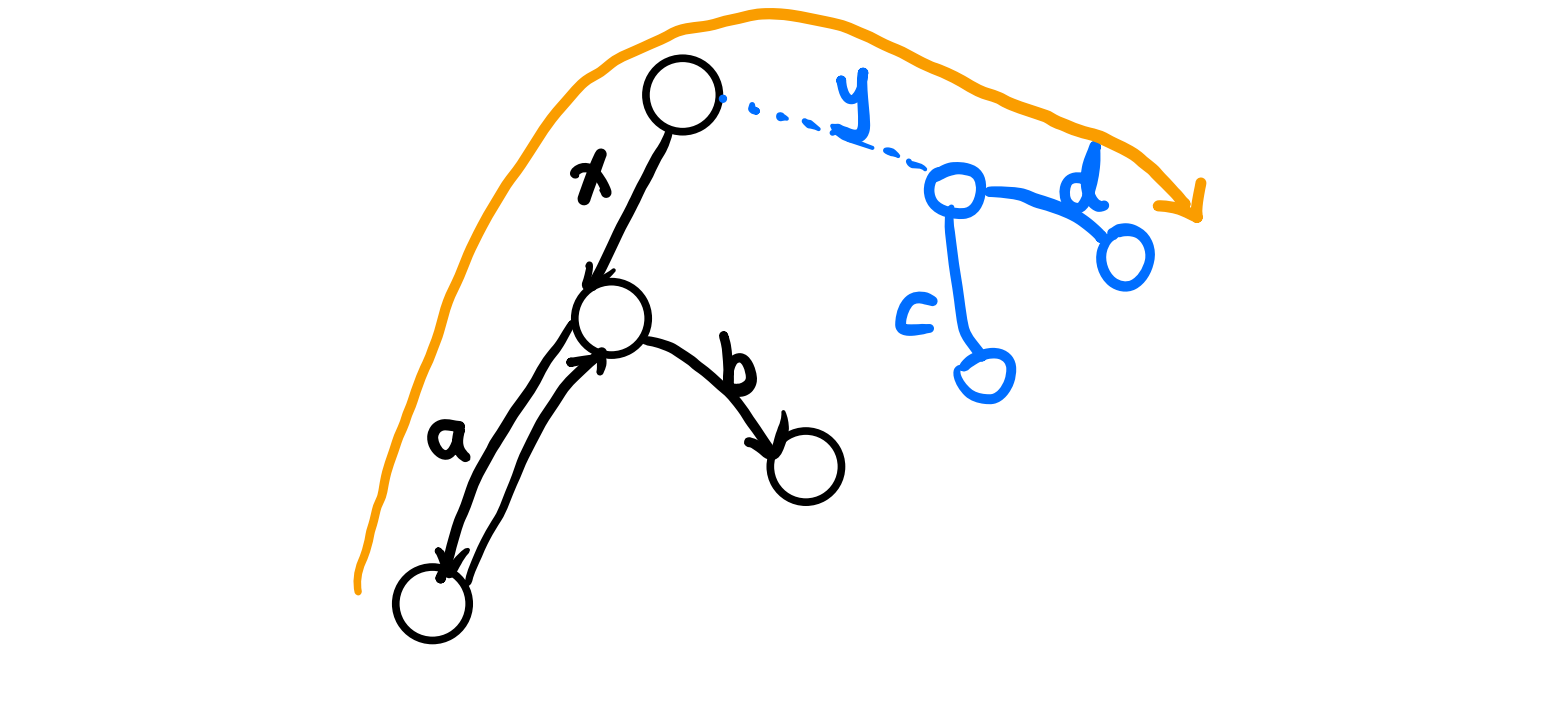
首先我们先抽线一下我们的过程，我们就是先从一点出发找到离他最远的另一点，再从找到的那一点出发找一条从它出发的最长的链。

树的直径示意图3

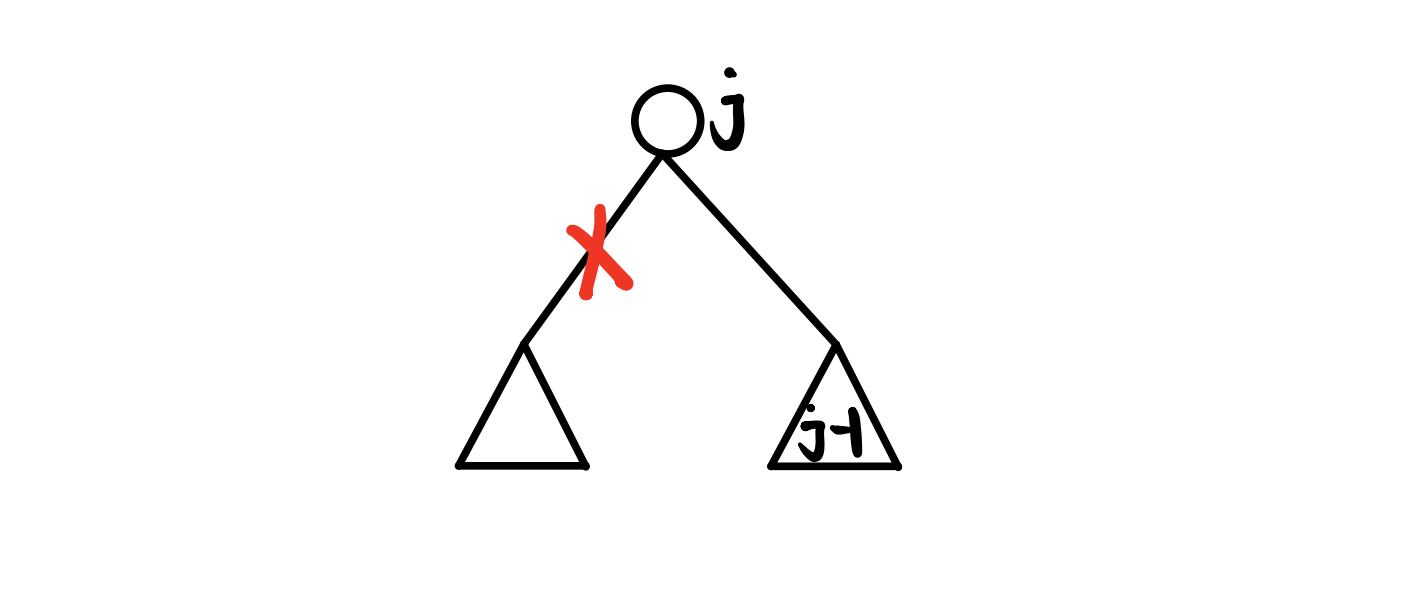
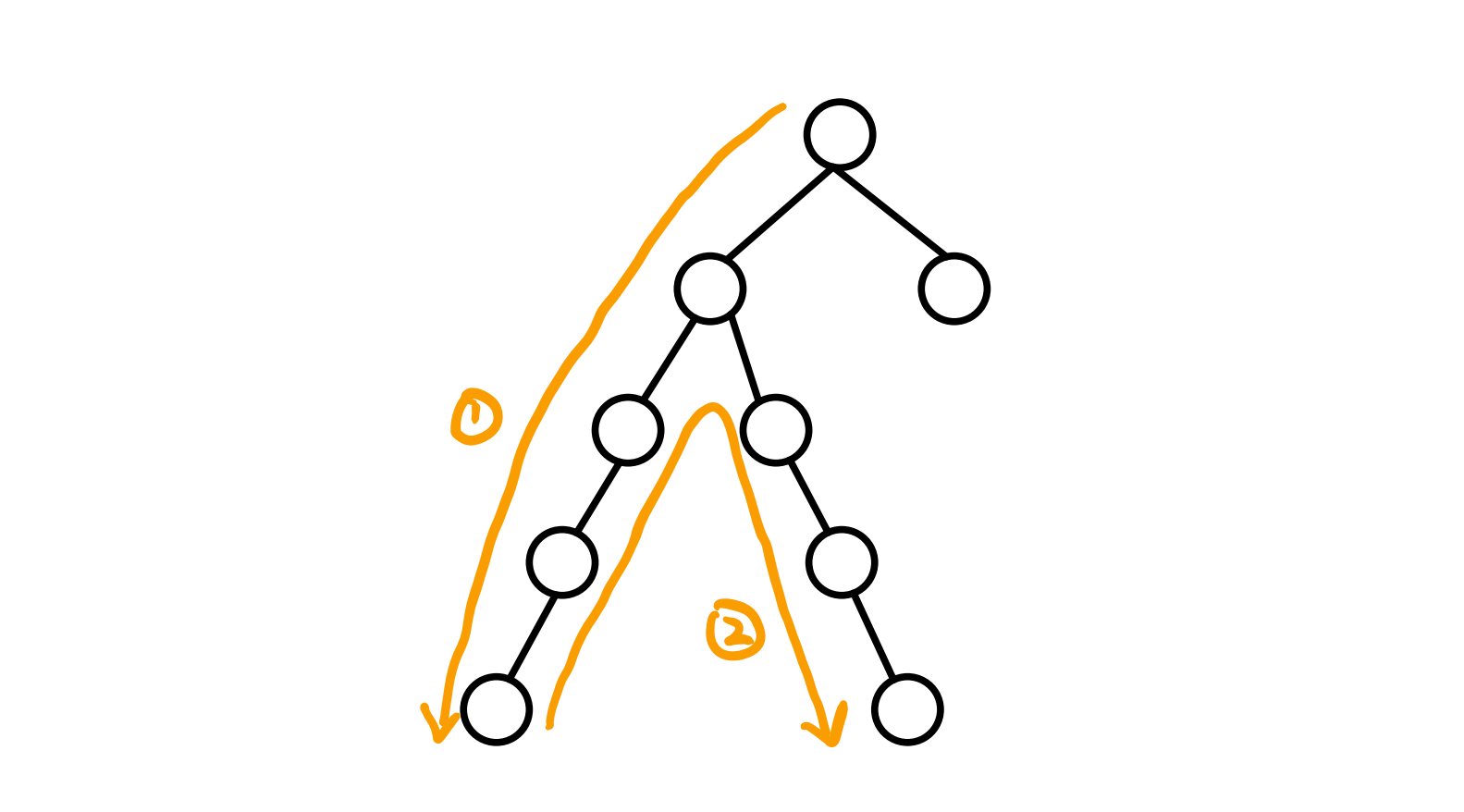
首先如果我们第一步找到的点在我们的最长链上，那答案一定是对的。下面我们证明我们第一步找到的点一定在我们的最长链上，若不然，我们分两种情况进行讨论：

  • 首先是真实的最长链和我们求出的最长链有交点，并相交在第一步求出的最长链上的情况。假如最长链如下图蓝色所示，假若它长于我们找到的黑色。首先由于我们第一遍找的是根开始的最长链，所以 \(a≥c\)，而第二遍我们是从找到的那一点出发找的最长链，所以 \(b≥d\)，所以 \(a+b≥c+d\)，这与假设的蓝色才是最长链 \(a+b<c+d\) 矛盾！

树的直径示意图4

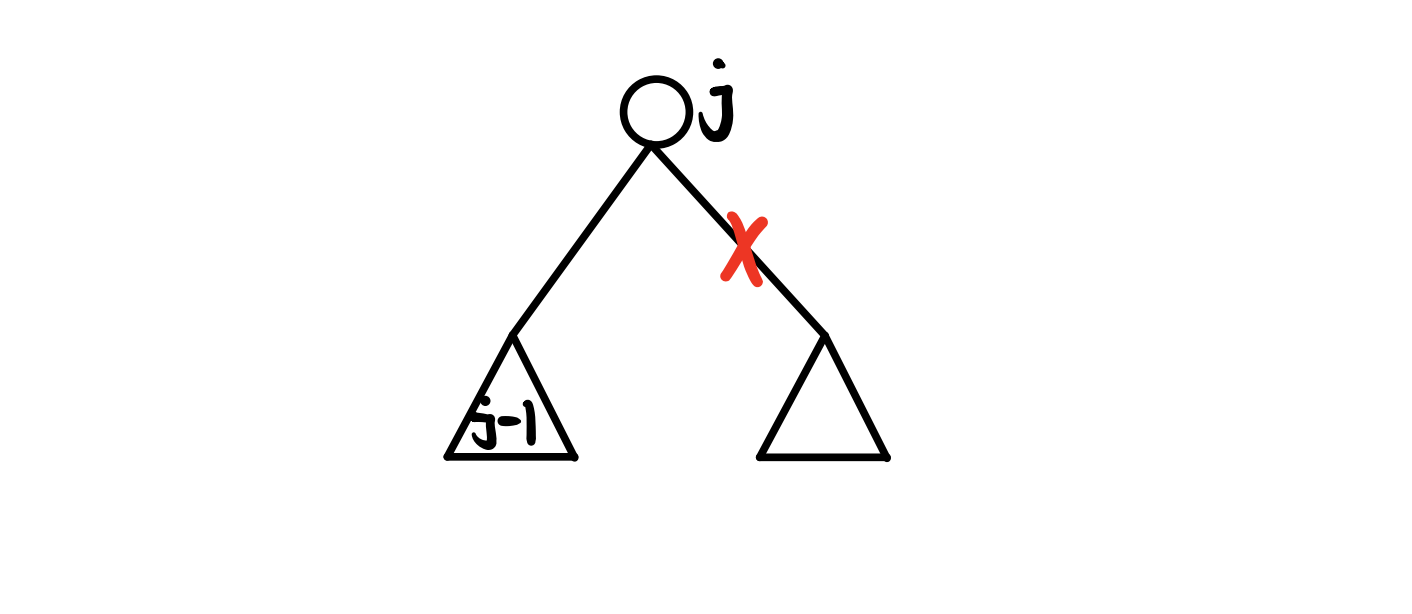
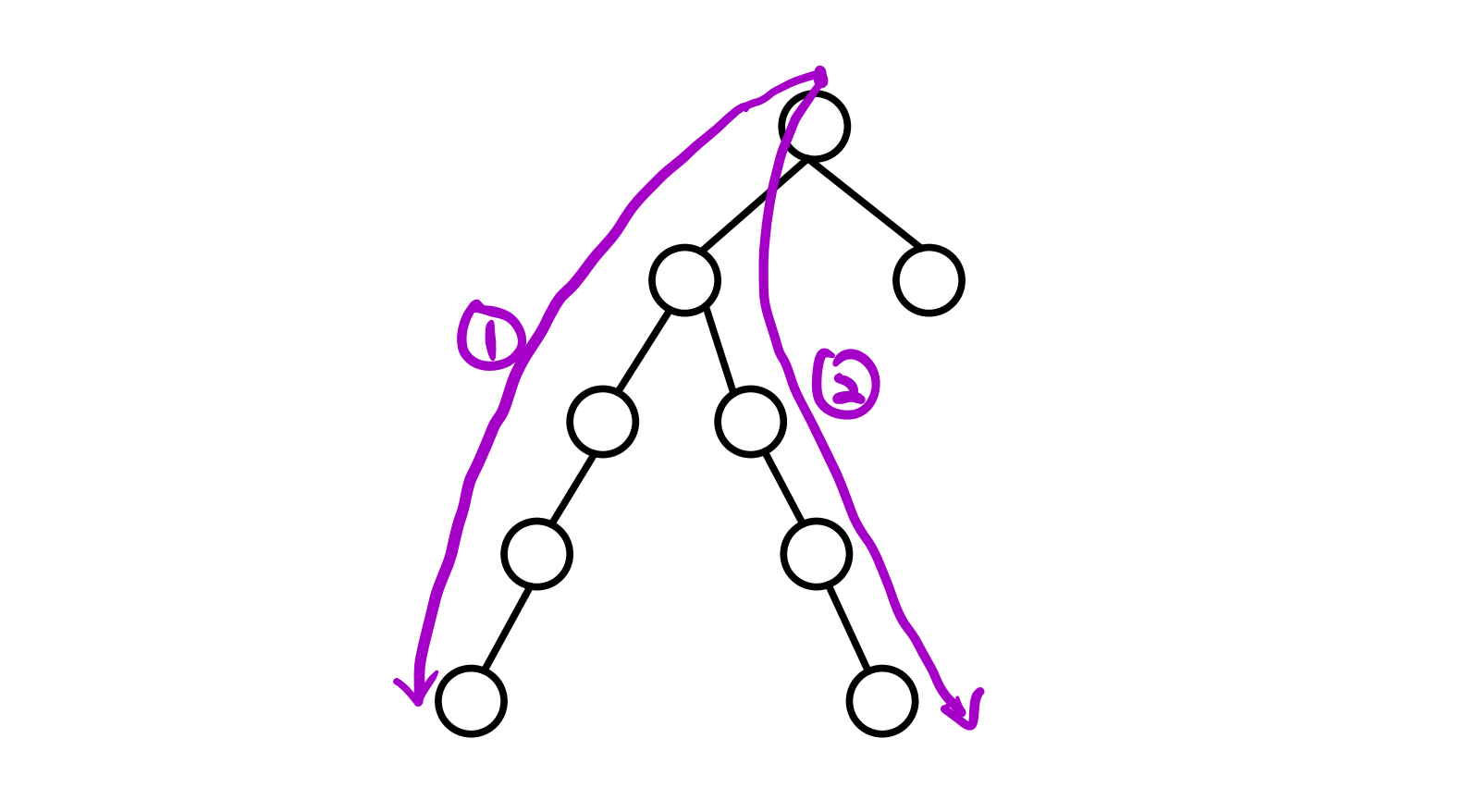
  • 接着是真实的最长链和我们求出的最长链有交点，并相交在第二步求出的最长链上的情况。假如最长链如下图蓝色所示，假若它长于我们找到的黑色。首先由于我们第一遍找的是根开始的最长链，所以 \(a≥c+t≥c\)​，而第二遍我们是从找到的那一点出发找的最长链，所以 \(b≥d+t≥d\)​，所以 \(a+b≥c+d\)​，这与假设的蓝色才是最长链 \(a+b<c+d\) 矛盾！

树的直径示意图5

  • 最后就是真实的最长链和我们求出的最长链没有交点的情况。假如最长链如下图蓝色所示，假若它长于我们找到的黑色。不失一般性，我们不妨设 \(d≥c\)，这时我们另一条链也就是我们橙色这条的长度为 \(L=a+x+y+d\) ，由于我们的 \(a+x\) 是从根出发的最长链，所以 \(a+x≥y+d\)，而 \(d≥c\)，所以

    \(L = a + x + y + d \ge y + d+ y+d \ge 2y + c + d > c + d\) ，

    这与 \(c+d\)​​ 是最长链相矛盾！从另一个角度我们也能分析出矛盾，我们知道 \(a+x\)​​ 是从根出发的最长链，所以 \(a≥b\)​，而 \(c+d>a+b\)​，而不妨设 \(d≥c\)​，此时至少有 \(d>b\)​，所以 \(x+y+d>b\)，所以 \(L=a+x+y+d>a+b\) ，这与 \(a+b\) 是从我们第一次搜索找到的点出发的最长链相矛盾！

树的直径示意图6

综上所述两遍 DFS 的方法的正确性是无可否认的。

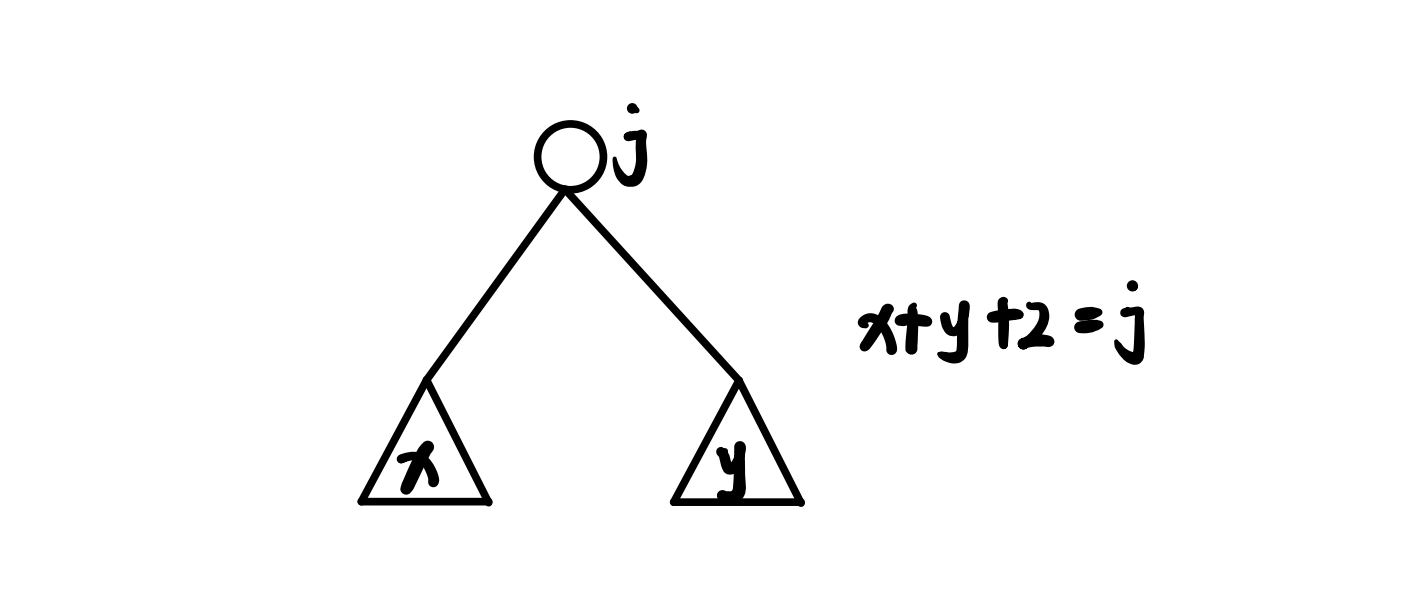
搞定了 DFS 后，接下来我们考虑我们如何使用树形动态规划的方法来解决这个问题。首先我们知道我们最后的答案一定是如我们那个抽象的图一样是从一个低点上升到最高点再下降的，而上升下降两条边一定是这个最高点的两条最长边。我们由此得到启示，我们设 \(f[i]\)​​​​ 表示 \(i\)​​​​ 号点向子树的最长链的长度，我们一遍 DFS 进行 DP，我们先递归处理 \(i\)​​​​ 的所有儿子 \(k\)​​​​，然后用 \(max(f[k])+a[i]\)​​​ 来更新 \(f[i]\)​​​，其中 \(a[i]\)​​​ 是 \(i\)​​​ 号点的权值。然后我们用最大的和次大的 \(f[k^′]\)​​ 和 \(f[k^{″}]\)​ 来更新答案 \(ans=max(ans,f[k^′]+f[k^{″}]+a[i])\)。这样我们就能求出我们树的直径了。

当然其实不是点权而是边权的情况也能轻松完成，毕竟点权和边权是可以通过点边转换来互相转换的。

Rinne Loves Edges

Description

$Rinne$ 最近了解了如何快速维护可支持插入边删除边的图，并且高效的回答一下奇妙的询问。 她现在拿到了一个 $n$ 个节点 $m(m=n-1)$ 条边的无向连通图，每条边有一个边权 现在她想玩一个游戏：选取一个 “重要点” $S$ ，然后选择性删除一些边，使得原图中所有除 $S$ 之外度为 $1$ 的点都不能到达 $S$。
定义删除一条边的代价为这条边的边权，现在 $Rinne$ 告诉你他选取的“重要点” 是谁，她想知道完成这个游戏的最小的代价，这样她就能轻松到达 $rk1$ 了！作为回报，她会让你的排名上升一定的数量。


4月份做每日一题时写的题解：Here

首先我们发现这是一个 \(n\)​ 个节点 \(n−1\)​ 条边的无向连通图，所以也就是一棵树。由于重要点已知，所以我们我们的问题就变成了我们设重要点为根，我们要删除最小权值的一系列边，使得根与每一个叶子都不连通。如果考虑吧在 \(i\)​ 这个点的子树上实现每个叶子都和 \(S\)​ 不连通，那么有两种情况，一是直接把 \(i\) 和它的儿子断开；而是在 \(i\) 的子树上以及实现了所有叶子节点无法通到 \(i\) .

所以我们就可以顺势设出 \(f[i]\)​ 表示以 \(i\)​ 为根的子树上所有的叶子都和根断开的最小代价，所以 \(f[i]=∑(min(f[k],dis[i][k]))\)，其中 \(k\) 是 \(i\) 的儿子，\(dis[i][k]\) 是 \(i\) 到 \(k\)​ 的边权。

这道题到这也轻松的解决了。我们下面来考虑一下这道题的一个变型，下面是题目描述：

Description

$Rinne$ 最近了解了如何快速维护可支持插入边删除边的图，并且高效的回答一下奇妙的询问。 她现在拿到了一个 $n(1\le n\le 1000)$ 个节点 $m(m=n-1)$ 条边的无向连通图，每条边有一个边权 $w_i$ 现在她想玩一个游戏：选取一个 “重要点” $S$，然后选择性删除一些边，使得原图中所有除 $S$ 之外度为 $1$ 的点都不能到达 $S$。
定义删除一条边的代价为这条边的边权，由于能力有限，切断边的总代价不能超过 $m$，且要让切断边中最大的代价最小。问在能力有限的条件下，切断边中最大的代价的最小值是多少？


题目链接：Here

首先有一个很容易想到的错误做法，就是我们把边进行排序，然后从小的开始删。但因为有总长度限制，这种删法又可能会删除一些多余的边，比如断开一个子树时，这个子树里面已经有被我删的边了，就可能达不到它能力 \(m\)​ 的限制，所以是不太对的。

一看到最大值最小，是不是 DNA 就动起来了，没错就是二分的思想。我们去二分能切的最长的边的代价，这时我们就把我们的边分成了能切断的和不能切断的。这时我们跑上面的那个动态规划，假设这时二分到 \(x\)​​​​ 我们设 \(f[i]\)​​​ 表示以 \(i\)​​ 为根的子树上所有的叶子都和根断开的最小代价，所以当 \(k\)​​ 是 \(i\)​ 的儿子时，若 \(dis[i][k]≤x\)​，也就是这条边时可以切断的时候，\(f[i]+=min(f[k],dis[i][k])\)，反之只能 \(f[i]+=f[k]\) 将断开的任务交给下面了。

我们最后看看答案 \(ans\) 是否满足 \(ans≤m\)​​ 来判断我们的二分怎么移动就可以完成这道题了。

\[QAQ \]

最后还有两道题分别是：HDU 3586 和 POJ 2152

这里稍微提一下思路，

HDU 3586：最小化最大值（二分），对上限进行二分，用树形DP去判断；

POJ 2152：

参考文章

posted @ 2021-08-19 21:12  RioTian  阅读(15969)  评论(1)  编辑  收藏  举报