AtCoder Beginner Contest 214 （D并查集，E反悔贪心，F公共子序列DP）

题目链接：Here

ABC水题，

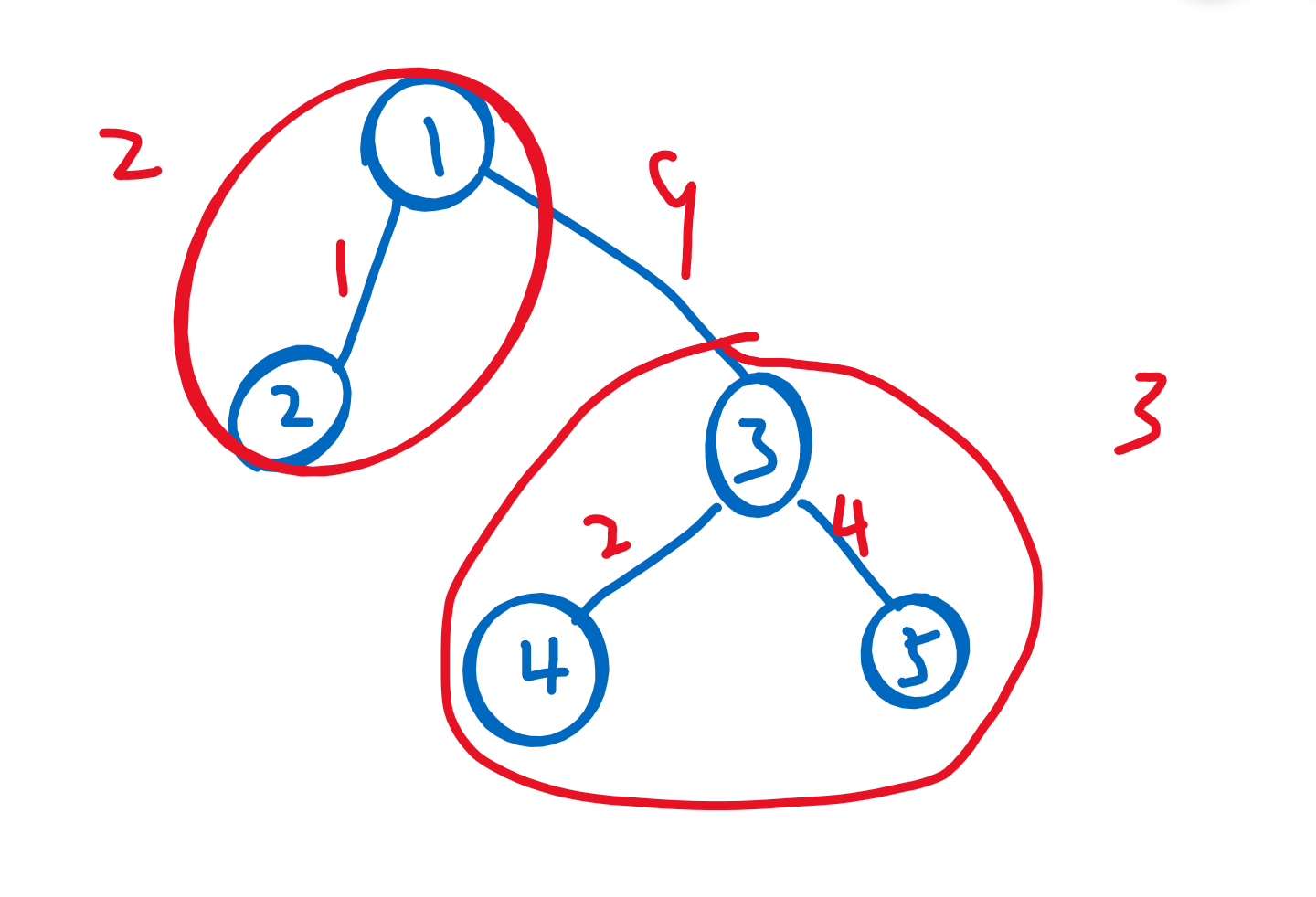
D - Sum of Maximum Weights

上图中最大权 $9$ 对答案的贡献是这条边两边的连通块的 size 的乘积再乘以 9

受到上面的启发，我们可以把每条边按边权大小从小到大排序。对于每条边（边权记为 $w$ ），先求出当前边连接的两个 group 的 size，不妨记为 $s i z e_{a}$ 和 $s i z e_{b}$ ，再把 $s i z e_{a} \times s i z e_{b} \times w$ 累加后合并两个连通块(并查集)

这里偷懒用一下 atcoder 的库函数写。

#include <bits/stdc++.h>
#include <atcoder/all>
using namespace std;
using namespace atcoder;

int main() {
    int n;
    cin >> n;
    vector<tuple<long long, int, int>> p(n - 1);
    for (auto &[w, u, v] : p) {
        cin >> u >> v >> w;
        u--; v--;
    }
    sort(p.begin(), p.end());
    long long ans = 0;
    dsu uf(n);
    for (auto [w, u, v] : p) {
        if (!uf.same(u, v)) {
            ans += w * uf.size(u) * uf.size(v);
            uf.merge(u, v);
        }
    }
    cout << ans << endl;
    return 0;
}

E - Packing Under Range Regulations

题意理解来自 Ncik桑

本题显然是区间调度问题(反悔贪心问题)，和以下问题等价：

有 $N$ 个工作。第 $i$ 个工作可以从 $L_{i}$ 日开始，截止日期为 $R_{i}$ 日。任何一项工作都可以在一天内完成，一天最多只能完成一项工作。你能在截止日期前完成所有工作吗？

显而易见的，我们应该从最紧急的工作开始，即把任务按 $L$ 从大到小排列然后用优先级队列按 $R$ 的大小顺序检索 “你现在可以做的任务 “来模拟这种情况。

const int inf = 1001001001;
void solve() {
    int n; cin >> n;
    vector<pair<int, int>> a(n);
    for (auto &[u, v] : a) cin >> u >> v;
    sort(a.begin(), a.end());
    priority_queue<int, vector<int>, greater<int>>q;
    int x = 1;
    a.push_back({inf, inf});
    for (auto [l, r] : a) {
        while (x < l && q.size()) {
            if (q.top() < x) {
                cout << "No\n";
                return ;
            }
            q.pop(); x += 1;
        }
        x = l; q.push(r);
    }
    cout << "Yes\n";
}

F - Substrings

首先，让我们考虑不受相邻字符不同时选择的约束的问题。

查找S的非空子字符串的数目。在这里，子字符串是在删除0个或更多字符的情况下不重新排序原始字符串的串联。

在这里，重要的是不同的删除方式可能会导致相同的子字符串。这里会用“公共子序列DP”的方法解决问题，在该方法中，子字符串的计数不包含那些重复项。
考虑下面的DP。

考虑下面的DP

$d p_{i}$ := 字符串中第 $1$ 个到第 $i$ 个字符串的数目，

定义 $d p_{p_{0}} = 1$ 对应于一个空字符串。转换可以写为以下内容：

$d p_{i} = \sum_{j = 0}^{i - 1} d p_{j}$

但可能会多次计算相同子字符串，所以稍微修改一下

$d p_{i} = \sum_{j = k}^{i - 1} d p_{j}$ ，其中 $k$ 为最大整数使得 $S_{i} = S_{k} (k < i)$ 如果没有这样的整数则 $k = 0$

直观地说，如果 $S_{k} = S_{i}$ ，那么我们禁止在某些 $j (< k)$ 的 $S_{j}$ 后面追加 $S_{i}$ ，因为这没有意义（我们可以在 $S_{j}$ 后面追加 $S_{k}$ ），这样就避免了重复。事实上，这是计算所有不重复的子字符串所需的唯一扭曲。

乍一看，复杂度看起来像 $O (| S |^{2})$ ，但实际上，借助累积和，它可以总共执行 $O (| S |)$ ，或者在没有累积和的情况下执行 $O (σ | S |)$ ，其中 $σ$ 表示不同字母的数量，这足够快了。

这个想法也可以应用于原始问题。设 $d p_{0} = 1$ 和 $d p_{1} = 0$ 。

递归关系可以写成： $d p_{i + 1} = \sum_{j = k}^{i - 1} d p_{j}$ ，其中 $k$ 是最大整数，使得 $S_{i} = S_{k}$ 和 $k < i$ （如果没有这样的整数，则 $k = 0$ ）

const int mod = 1e9 + 7;
int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    string s; cin >> s;
    int n = s.size();
    vector<ll> f(n + 2); f[0] = 1;
    for (int i = 0; i < n; ++i)
        for (int j = i - 1;; j--) {
            f[i + 2] = (f[i + 2] + f[j + 1]) % mod;
            if (j == -1 || s[j] == s[i]) break;
        }
    ll ans = 0;
    for (int i = 2; i < n + 2; i++) ans += f[i];
    cout << ans % mod << "\n";
}