2021暑假训练赛1 基于Codeforce#479(div3)
A - Xor Sum
似乎是很明显的字典树问题(不会啊,最后搬了一个板子修修改改以后才过了
AcWing 相似题目:143. 最大异或对
最后得吐槽一下 memset 为什么能这么慢啊 Kora!
改手动初始化之后从 TLE 降到 500ms
const int MAXN = 100005;
int tire[MAXN * 32][2];
ll arr[MAXN * 32], s;
int n, m;
int pos = 1;
void insert(ll s) {
int root = 0;
for (int i = 31; i >= 0; i--) {
int x = (s >> i) & 1;
if (tire[root][x] == 0)
tire[root][x] = pos++;
root = tire[root][x];
}
arr[root] = s;
}
ll search(ll s) {
bool flag = false;
int root = 0;
for (int i = 31; i >= 0; i--) {
int x = (s >> i) & 1;
if (tire[root][!x]) root = tire[root][!x];
else root = tire[root][x];
}
return arr[root];
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int T, Case = 1;
cin >> T;
while (T--) {
cin >> n >> m;
while (n--) {
cin >> s;
insert(s);
}
cout << "Case #" << Case++ << ":" << endl;
while (m--) {
cin >> s;
cout << search(s) << endl;
}
for (int i = 0; i < MAXN; ++i) arr[i] = 0;
for (int i = 0; i < MAXN; ++i) for (int j = 0; j < 2; ++j) tire[i][j] = 0;
}
return 0;
}
B - Wrong Subtraction (签到)
过于谨慎了,签到题情况都想全了还是自测半天数据。
\(k\) 不大,直接暴力模拟
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
ll n, k; cin >> n >> k;
for (int i = 1; i <= k; ++i) {
int t = n % 10;
if (t == 0) n /= 10;
else n--;
}
cout << n;
}
C - Two-gram
为什么会理解错题意啊?!!
子串必须由相邻的两个字符组成。 说明字串长度为 \(2\) 啊
关于 string 似乎只能 push_back 加入字符了,
直接写 t = s[i] + s[i + 1] 会乱码
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n; string s;
cin >> n >> s; n -= 1;
int cnt = 0; string t = "";
for (int i = 0; i < n; i++) {
int ccnt = 1;
for (int j = i + 1; j < n; j++)
if (s[j] == s[i] && s[j + 1] == s[i + 1])
ccnt++;
if (ccnt > cnt) {
cnt = ccnt;
string tmp;
tmp.push_back(s[i]), tmp.push_back(s[i + 1]);
t = tmp;
}
}
cout << t << endl;
return 0;
}
E - Divide by three, multiply by two
看样例发现一个规律 12 4 8 16
关于 3 的因子个数,如果因子个数多的放在前面,因子数相同的话将小值排前
因为题目保证一定存在符合题意的组合,那么这种写法一个可以
const int N = 1e2 + 10;
ll a[N];
ll fun(ll n) {
ll cnt = 0;
while (n % 3 == 0) {cnt += 1, n /= 3;}
return cnt;
}
bool cmp(ll x, ll y) { return fun(x) == fun(y) ? x < y : fun(x) > fun(y);}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n; cin >> n;
for (int i = 0; i < n; ++i) cin >> a[i];
sort(a, a + n, cmp);
for (int i = 0; i < n; ++i) cout << a[i] << " \n"[i == n - 1];
}
F - Cyclic Components
很可惜,这道题做出了就AK了。
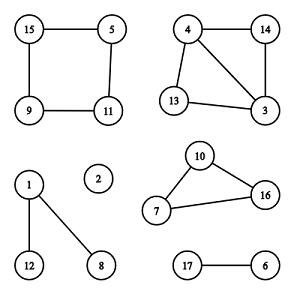
关于 简单环,在上图中只有 $[7,10,16],[5,11,9,15] $ 两个环符合条件,
即环内每个点的度当且仅当为 \(2\)
那么我们存边和度再跑DFS即可
const int N = 2e5 + 10;
vector<int>e[N];
bool vis[N];
int flag ;
void dfs(int u) {
vis[u] = 1;
if (e[u].size() != 2) flag = 0; // 如果 环内度数不为 2 则标记置为 0
for (auto v : e[u]) {
if (vis[v]) continue;
dfs(v);
}
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n, m; cin >> n >> m;
for (int i = 1, u, v; i <= m; ++i) {
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
int ans = 0;
for (int i = 1; i <= n; ++i) {
if (vis[i]) continue;
flag = 1;
dfs(i);
ans += flag;
}
cout << ans;
}
G - Consecutive Subsequence
看完题目知道是一道最长上升子序列题,但普通的DP似乎处理不了,因为:序列是连续的。
所以 DP 转移方程应该写为 \(f_i = max(f_{i - 1} + 1,f_i)\)
- \(\mathcal{O}(n)\)
ll a[N];
map<ll, int>mp;
int len, lst, n;
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
cin >> n;
for (int i = 0; i < n; ++i) {
cin >> a[i];
int cnt = mp[a[i]] = mp[a[i] - 1] + 1;
if (cnt > len) len = cnt, lst = a[i];
}
int tmp = lst - len + 1;
cout << len << "\n";
for (int i = 0; i < n; ++i)
if (a[i] == tmp) {
cout << i + 1 << " ";
tmp += 1;
}
return 0;
}



