区间DP练习题题解
算法讲解：Here
AcWing 282. 石子合并 （模板）
题目链接：Here
const int N = 310;
int a[N], s[N];
int dp[N][N];
void solve() {
int n; cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
s[i] += s[i - 1] + a[i];
}
// 区间 DP 枚举套路：长度+左端点
for (int len = 1; len < n; ++len) {// len表示i和j堆下标的差值
for (int i = 1; i + len <= n; i ++) {
int j = i + len; // 自动得到右端点
dp[i][j] = 1e8;
for (int k = i; k <= j - 1; k ++) { // 必须满足k + 1 <= j
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1]);
}
}
}
cout << dp[1][n] << "\n";
}
「NOIP2006」能量项链 （环形石子合并）
题目链接：Here
题面
在Mars星球上，每个Mars人都随身佩带着一串能量项链。在项链上有N颗能量珠。能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。因为只有这样，通过吸盘（吸盘是Mars人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为m，尾标记为r，后一颗能量珠的头标记为r，尾标记为n，则聚合后释放的能量为 $m*r*n$（Mars单位），新产生的珠子的头标记为m，尾标记为n。需要时，Mars人就用吸盘夹住相邻的两颗珠子，通过聚合得到能量，直到项链上只剩下一颗珠子为止。显然，不同的聚合顺序得到的总能量是不同的，请你设计一个聚合顺序，使一串项链释放出的总能量最大。
思路1：
(2,3) (3,5) (5,10) (10,2)
换种表达方式
2 3 5 10 2
所以实际还要往后面乘一个数，这样缺点？
这样表达方式也要学习。一开始自己的想法居然是利用pair, 然后预处理，看来还是要多观察数据的特性
\(f[l,r]\) 所有将 \([l,r]\) 合并的方式的Max
这种划分方式，中间是公用的！
\(f[l,r] = max(f[l,r], f[l,k]+f[k,r]+w[l]w[k]w[r])\)
特殊情况解释：
- 如何只有一个矩阵，代价为0，len从3开始枚举没问题
- 最后一次合并相当于\([l,k],[k,r]\)
把合并n颗珠子的问题转化为合并 \((n+1)\) 个数合并的问题，只不过有一个数是公用的，注意不要间断分割
区间长度为：\(n + 1\)
const int N = 210;
int a[N], f[N][N];
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n; cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
a[i + n] = a[i];
}
//长度为3实际上只是包含了2颗珠子的首尾信息
for (int len = 3; len <= n + 1; ++len)
for (int i = 1; i + len - 1 <= 2 * n; ++i) {
int j = len + i - 1;
for (int k = i + 1; k < j; ++k) // 最长的串，只计算一边的内容，所以l+1
f[i][j] = max(f[i][j], f[i][k] + f[k][j] + a[i] * a[k] * a[j]);
//这里不能间断分割，因为有一个公用的量，同石子合并不同
}
int ans = INT_MIN;
for (int i = 1; i <= n; ++i) ans = max(ans, f[i][i + n]);
// 注意这里实际上默认的是长度公式为n+1
cout << ans << '\n';
}
思路2：直接当成珠子来看待即可，模拟合并过程。区间长度为：\(n\)
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 210;
int a[N], f[N][N];
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n; cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
a[i + n] = a[i];
}
for (int len = 1; len <= n; ++len)
for (int i = 1; i + len - 1 <= n * 2; ++i) {
int j = len + i - 1;
if (len == 1) f[i][j] = 0;
//这里的过程同石子合并，这里不难想到若将l到k的珠子合并之后会变成一个首是l而尾k+1的珠子；
//同理若将k+1到r的珠子合并之后会变成一个首是k+1而尾r+1的珠子；
for (int k = i; k < j; ++k)
f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j] + a[i] * a[k + 1] * a[j + 1]);
}
int ans = INT_MIN;
for (int i = 1; i <= n; ++i) ans = max(ans, f[i][i + n - 1]);
cout << ans << '\n';
}
AcWing 283. 多边形
题目链接：Here
这是一个标准的区间DP问题，这个题跟石子合并非常相似，只不过它是一个环形结构，所以形成一个2倍长度的链就可以很好的解决环形区间DP问题。
代码只是照着算法竞赛进阶指南的思路和之前总结的模板手撸了一遍，而且写的好像有点蠢就不放了
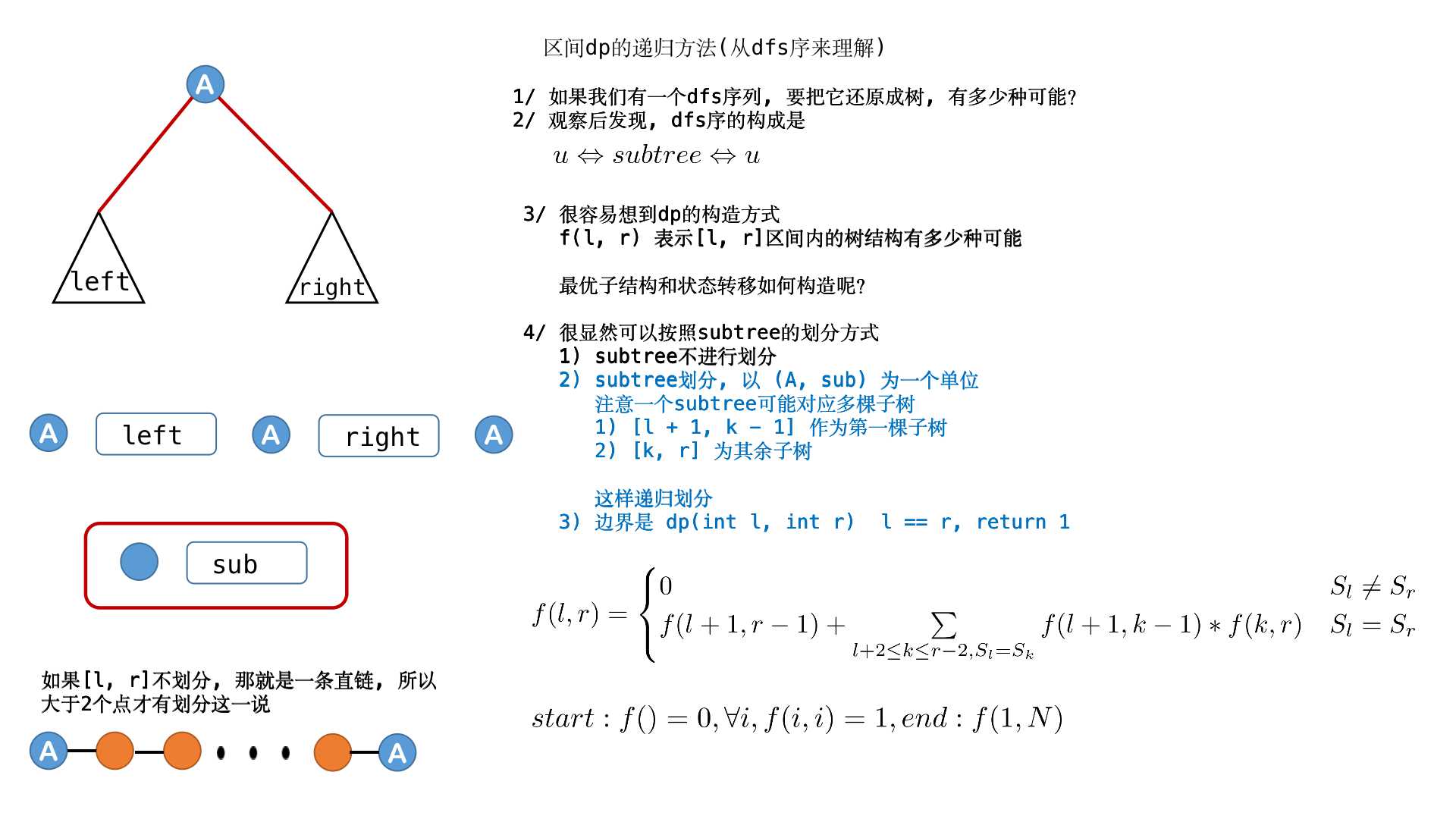
AcWing 284. 金字塔 (区间dp的递归算法和记忆化搜索)
题目链接：Here
const int N = 310, mod = 1e9;
char str[N];
int n;
int f[N][N];
int dp(int l, int r) {
if (l > r) return 0;
if (l == r) return 1;
int& ans = f[l][r];
if (ans != -1) return ans;
ans = 0;
if (str[l] == str[r])
for (int k = l + 2; k <= r; k++)
ans = (ans + (ll)dp(l + 1, k - 1) * (ll)dp(k, r)) % mod;
return ans;
}
void solve() {
cin >> str + 1;
n = strlen(str + 1);
memset(f, -1, sizeof(f));
cout << dp(1, n) << "\n";
}
AcWing 321. 棋盘分割
题目链接：Here
using namespace std;
typedef long long llong;
typedef set<int>::iterator ssii;
#define Cmp(a, b) memcmp(a, b, sizeof(b))
#define Cpy(a, b) memcpy(a, b, sizeof(a))
#define Set(a, v) memset(a, v, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define _forS(i, l, r) for(set<int>::iterator i = (l); i != (r); i++)
#define _rep(i, l, r) for(int i = (l); i <= (r); i++)
#define _for(i, l, r) for(int i = (l); i < (r); i++)
#define _forDown(i, l, r) for(int i = (l); i >= r; i--)
#define debug_(ch, i) printf(#ch"[%d]: %d\n", i, ch[i])
#define debug_m(mp, p) printf(#mp"[%d]: %d\n", p->first, p->second)
#define debugS(str) cout << "dbg: " << str << endl;
#define debugArr(arr, x, y) _for(i, 0, x) { _for(j, 0, y) printf("%c", arr[i][j]); printf("\n"); }
#define _forPlus(i, l, d, r) for(int i = (l); i + d < (r); i++)
#define lowbit(i) (i & (-i))
const int N = 8;
const int maxn = 15 + 2;
int f[maxn][N + 2][N + 2][N + 2][N + 2];
int A[N + 2][N + 2];
int n;
int S[N + 2][N + 2];
double tot = 0;
const int inf = 0x3f3f3f3f;
void init() {
Set(f, inf);
Set(S, 0);
_rep(i, 1, N) _rep(j, 1, N) {
S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + A[i][j];
}
_rep(x1, 1, N) _rep(y1, 1, N) {
_rep(x2, x1, N) _rep(y2, y1, N) {
int t = S[x2][y2] - S[x2][y1-1] - S[x1-1][y2] + S[x1-1][y1-1];
f[0][x1][y1][x2][y2] = t * t;
}
}
}
void dp(int k, int x1, int y1, int x2, int y2) {
int& ans = f[k][x1][y1][x2][y2];
ans = inf;
_for(a, x1, x2) {
ans = min(ans, f[k-1][x1][y1][a][y2] + f[0][a+1][y1][x2][y2]);
ans = min(ans, f[k-1][a+1][y1][x2][y2] + f[0][x1][y1][a][y2]);
}
_for(b, y1, y2) {
ans = min(ans, f[k-1][x1][y1][x2][b] + f[0][x1][b+1][x2][y2]);
ans = min(ans, f[k-1][x1][b+1][x2][y2] + f[0][x1][y1][x2][b]);
}
}
int main() {
freopen("input.txt", "r", stdin);
scanf("%d", &n);
_rep(i, 1, N) _rep(j, 1, N) {
scanf("%d", &A[i][j]);
tot += A[i][j];
}
init();
_rep(k, 1, n - 1) _rep(x1, 1, N) _rep(y1, 1, N) {
_rep(x2, x1, N) _rep(y2, y1, N) {
dp(k, x1, y1, x2, y2);
}
}
double avr = (double)(tot / n);
//debug(tot);
double ans = sqrt(1.0 * f[n - 1][1][1][N][N] / n - (avr * avr));
printf("%.3f\n", ans);
}
另外一种思路：
完成划分后，一共会得到 \(n\) 块棋盘。
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。
现在需要把棋盘按上述规则分割成 \(n\) 块矩形棋盘，并使各矩形棋盘总分的均方差最小。
显然可以观察到一个二维 区间 dp 的模型 （不对，二维是不是应该叫面积DP(滑稽)）
根据题意，我们可以得到的信息是
1)一共可以对棋盘进行 \(n−1\) 次划分得到 \(n\) 个子棋盘
2)对所有的子棋盘可以求得的平均数 \(\bar x=\frac{∑\limits^n_{i=1}x^i}n\)
3)要求总分的均方差最小 \(σ= \sqrt{\frac{\sum\limits_{i=1}^n(x_i-\bar x)^2}n}\)
/*
1.1) 横着切:
1.1.1)以(x1, y1)为左上角，以(x1, y2)为右下角 或 以(x1+1, y1)为左上角，以(x2, y2)为右下角
1.1.2)以(x1, y1)为左上角，以(x1+1, y2)为右下角 或 以(x1+2, y1)为左上角，以(x2, y2)为右下角
......
1.1.i)以(x1, y1)为左上角，以(x1+i, y2)为右下角 或 以(x1+i+1, y1)为左上角，以(x2, y2)为右下角
......
1.1.x2-1)以(x1, y1)为左上角，以(x2-1, y2)为右下角 或 以(x2, y1)为左上角，以(x2, y2)为右下角
1.2) 竖着切:
1.2.1)以(x1,y1)为左上角，以(x2, y1)为右下角 或 以(x1, y1)为左上角，以(x2, y2)为右下角
1.2.2)以(x1,y1)为左上角，以(x2, y1+1)为右下角 或 以(x1, y1+2)为左上角，以(x2, y2)为右下角
......
1.2.i)以(x1,y1)为左上角，以(x2, y1+i)为右下角 或 以(x1, y1+i+1)为左上角，以(x2, y2)为右下角
......
1.2.y2-1)以(x1, y1)为左上角，以(x2, y2-1)为右下角 或 以(x1,y2-1)为左上角，以(x2, y2)为右下角
*/
2）状态转移方程
模拟上述集合的划分枚举所有的区间即可
由于dp的方程维数过大，写 \(5\) 重迭代太麻烦了，这题采用记忆化搜索
const int N = 9, M = 15;
const double INF = 1e9;
int n, m = 8;
int s[N][N];
double f[N][N][N][N][M];
double X; //均值x拔
double get(int x1, int y1, int x2, int y2) {
//根号下，求和符号内的部分
double sum = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] - X;
//还要平方
return (double)sum * sum;
}
double dp(int x1, int y1, int x2, int y2, int k) {
auto &t = f[x1][y1][x2][y2][k];
if (t >= 0) return t;
if (k == 1) return get(x1, y1, x2, y2);
t = INF; //求最小值要初始化成最大值
//横着切
for (int i = x1; i < x2; ++i) {
t = min(t, dp(x1, y1, i, y2, k - 1) + get(i + 1, y1, x2, y2));
t = min(t, dp(i + 1, y1, x2, y2, k - 1) + get(x1, y1, i, y2));
}
//竖着切
for (int i = y1; i < y2; ++i) {
t = min(t, dp(x1, y1, x2, i, k - 1) + get(x1, i + 1, x2, y2));
t = min(t, dp(x1, i + 1, x2, y2, k - 1) + get(x1, y1, x2, i));
}
return t;
}
int main() {
cin >> n;
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= m; ++j) {
cin >> s[i][j];
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
}
}
X = (double) s[m][m] / n;
//记忆化搜索，初始化成NaN
memset(f, -1, sizeof f);
//这个就是\sigma的完整计算公式
printf("%.3lf\n", sqrt(dp(1, 1, m, m, n) / n));
return 0;
}
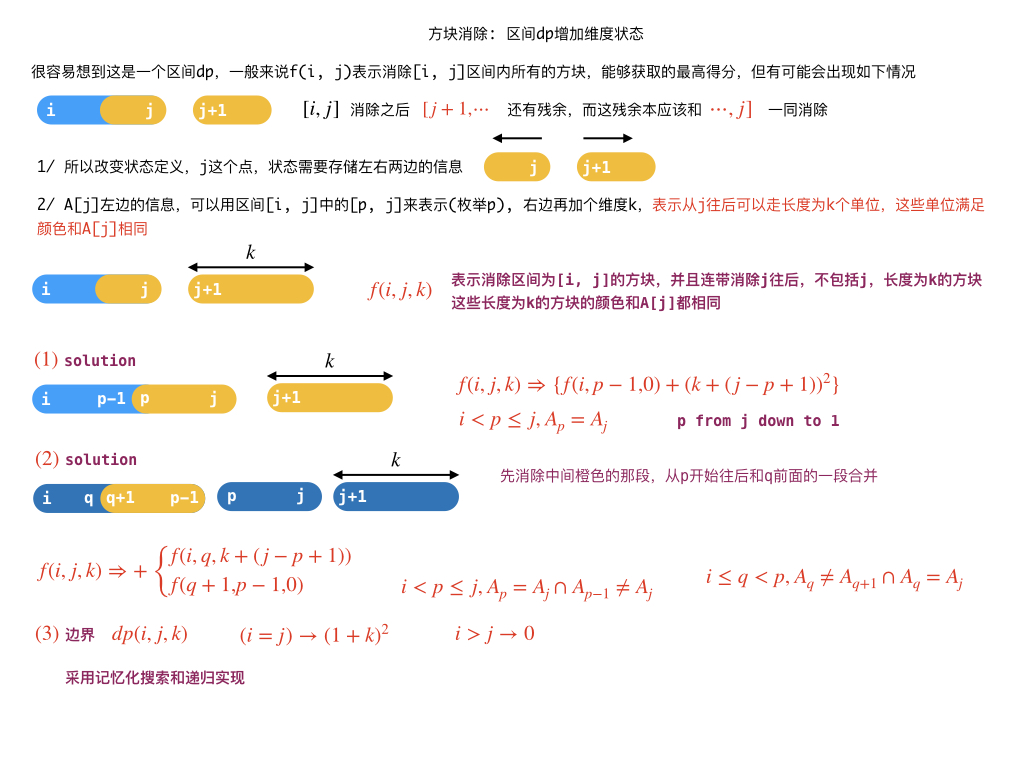
AcWing 322. 消木块 （困难）
题目链接：Here
#define _rep(i, l, r) for(int i = (l); i <= (r); i++)
#define _for(i, l, r) for(int i = (l); i < (r); i++)
const int maxn = 200 + 10;
int f[maxn][maxn][maxn];
int A[maxn];
int N;
void init() { Set(f, -1);}
int dp(int i, int j, int k) {
if(i > j) return 0;
int& ans = f[i][j][k];
if(i == j) return ans = (1 + k) * (1 + k);
if(ans >= 0) return ans;
int p = j;
while (p >= i && A[p] == A[j]) p--;
p++;
ans = dp(i, p-1, 0) + (k + j-p+1) * (k + j-p+1);
_for(q, i, p) {
if(A[q] == A[j] && A[q+1] != A[q]) {
ans = max(ans, dp(i, q, k+j-p+1) + dp(q+1, p-1, 0));
}
}
return ans;
}
int main() {
int T; scanf("%d", &T);
_rep(kase, 1, T) {
printf("Case %d: ", kase);
scanf("%d", &N);
_rep(i, 1, N) scanf("%d", &A[i]);
init();
// then dp()
printf("%d\n", dp(1, N, 0));
}
}
