【算法学习笔记】博弈论浅析之游戏类

一、取走游戏

​ 首先，我们介绍一下组合游戏。组合游戏是一种两个人参与的游戏，参与者拥有完整的（有关游戏的）信息，没有任何意外产生的操作(即保证无意外性)，并且游戏拥有一个输赢的结果。这样的游戏是由一系列的位置，包括一个起始位置，和哪个参与者进行下一步所组成、决定的。游戏在参与者的选择中从一步移向下一步，最终达到某个终点位置。这样的一个终点位置意味着没有任何下一步移动存在的可能。之后，其中一名游戏者被判定为胜利，另一名则为失败。
​ 这个理论可以被分为两个部分：公平游戏，游戏中对于两名参与者所被给定的任意一个位置，都能够到达其他所有的位置(强调两名参与者相同机会)。非公平游戏，则是被给定的不同位置对于两名参与者有着不同的机会，例如国际象棋。
在第一部分我们将只讨论有关于公平游戏的部分，下面讲一个简单的例子。

简单的取走游戏

我们来分析这样一个游戏，下面介绍下游戏规则：

1. 两名参与者，我们成为 A和B (懒得打罗马数字1和2)
2. 桌上有 \(21\) 根火柴。
3. 每次只能从火柴堆中拿下 \(1、2、3\) 根火柴
4. 参与者轮流拿火柴，A先手
5. 最后一个拿走剩下所有火柴的人赢

现在知道游戏规则了，我们就尝试着来分析这个游戏。想一想，其中一名参与者一定能够在游戏中胜利吗？我们要先手还是要后手？有什么很好的策略吗？

下面，我们将从后往前分析这个游戏，即从游戏即将结束的部分开始。这种方法被称为倒退归纳。

• 假设只剩下1、2、3根火柴，显然拿走剩下这几根火柴就赢了。
• 假设剩下4根火柴，那么这时候轮到拿火柴的人肯定输，因为怎么拿都会剩下，然后他的对手拿掉剩下的火柴就赢了。所以4根火柴的情况是先手必败。
• 那么，我们递推到5、6、7根火柴，显然，只要拿剩下4根，那么就让对手陷入先手必败状态。5、6、7根火柴便是先手必胜状态。那么若剩下8根火柴，这时候轮到的参与者肯定输，因为你只能拿到剩下5、6、7根火柴，让对手进入先手必胜的状态。
• 所以，我们发现，0，4，8，12，16„根火柴是一个目标状态。我们要争取使自己进入这个状态。现在我们便能分析21根火柴的游戏了，既然21不被4整除，第一个移动火柴的人（即先手者，参与者A）肯定赢。唯一的策略便是拿走一根火柴，剩下20根让对手绝望去。

究竟什么是组合游戏？

现在我们将组合游戏的概念定义得更准确一些。

组合游戏是一个满足下列情况的游戏：

1. 两名参与者 （经典 Alice 和 Bob）
2. 游戏中有一系列通常是有限个数的可能的情况或位置。
3. 游戏规则是对两名参与者同时有效的，并且每个位置向另一个位置移动都是合法的。如果规则对于两名参与者没有区别，也就是说两名参与者遇上同样的情况时，有着相同的选择个数和选择情况，那么这个游戏被称为一个公平游戏。否则，称为不公平游戏。
4. 参与者交替进行游戏
5. 游戏结束时，意味着到达一个终点。一般规则下，最后一次操作的人获胜，但在逆规则下，最后一次操作的人失败。这样的一个终点位置意味着没有任何下一步移动存在的可能。使游戏到达终点的人为胜者，另一个为败者。如果游戏不能结束，那么称为平局。然而，我们几乎总是添加一个结束位置。这样就避免了平局的可能性。
6. 游戏在有限步数内会结束，无论怎么进行。 我想很有必要提醒在这个定义中省略了什么：没有随机移动，比如掷骰子；一个组合游戏是一个拥有完整信息的游戏：同时移动和隐藏移动是不允许的；没有平局。

P 位置和 N 位置（先手必败状态和先手必胜状态)

回到刚刚说的取走游戏中，我们发现 $0，4，8，12，16... $ 是一个对于前一个操作的参与者胜利的位置(Previous Player)，而 \(1,2,3,5,6,7,9,10,11\) 是对现在或者说是下一个操作的参与者胜利的位置(Next Player or Now Player). 前者则称为P位置，后者称为N位置。(作者注：在下文中，P位置也会被称为先手必败状态，N位置也会被称为先手必胜状态)。在一个公平游戏中，我们可以找到规律，哪一个是先手必胜状态，哪一个是先手必败状态，只要从结束状态开始通过下列的操作进行倒推即可。

1. 每个结束状态都是先手必败状态。
2. 如果当前状态能够转移到先手必败状态(P位置)的状态，则这个状态为先手必胜状态（N位置）。
3. 如果当前状态所能转移到的所有状态都是先手必胜状态(N位置)，那么这个状态为先手必败态（P位置）。

而这样分析之后，很明显，任意一个处于P位置的人肯定会输，因为他只能转移到N位置。而处于N位置的人，只要转移到P位置就可以赢了。
从上面的推导，显然地，我们会发现对于N位置和P位置有一些性质，这些性质的前提是，这是公平游戏，且有终点。

1. 终点是P位置。
2. 所有P位置能转移到的都是N位置
3. N位置至少能转移到一个P位置

减法游戏

​ 现在我们把上面所提到的简单取走游戏一般化。设 \(S\) 表示一个正整数的集合，那么以S为减法集的减法游戏就是像这么玩的：有一堆 \(n\) 根火柴，每次像简单取走游戏一样拿去火柴，但是拿去的火柴数必须在减法集中。其他规则同减法游戏。
​ 那么，简单的取走游戏就是一个 \(S=\{1,2,3\}\) 的减法游戏。现在为了更好地说明，我们来讨论一个 \(S=\{1,3,4\}\) 的减法游戏。首先，(个数)0是终点，为 \(P\) 位置。而 \(1,3,4\) 则为 \(N\) 位置，因为可以转移到0这个 \(P\) 位置。2是 \(P\) 位置，因为2只能转移到1，而1为 \(N\) 位置。5,6是 \(N\) 位置，因为可以转移到2。7是P位置，因为7能转移到的是3,4,6，都是N位置。
按着这样子递推下去，我们会发现

\[P=\{0,2,7,9,14,16,...\} \\ N=\{1,3,4,5,6,8,10,11,12,13,15,...\} \]

我们会发现，\(PNPNNNN\) 是一个长度为7的循环节。现在，如果是 \(100\) 根火柴，先手赢还是后手赢？我们发现，\(100\ mod\ 7 = 2\)，对应循环节，\(2\) 是 \(P\) 位置，所以 \(100\) 根火柴是先手必败状态，后手肯定赢。

现在，请你尝试着分析一个\(S=\{1,2,3,4,5,6\}\) 的减法游戏，并搞清楚 \(10000\) 根火柴的话，先手赢还是后手赢？

《Game Theory》中有对应练习，请读者自行查找

二、Nim 游戏

游戏规则

​ Nim游戏是最有名的取走游戏。有三堆火柴，分别有 \(x_1,x_2,x_3\) 根火柴(比如 \(5,7,9\) )。两个人轮流进行操作，每次只能取走一堆火柴中任意数量的火柴，不能同时对多堆进行操作。和取走游戏一样，拿走剩下所有火柴的人获胜。

初步分析

​ 我们用(\(x_1,x_2,x_3\))表示对应三堆分别有 \(x_1,x_2,x_3\) 根火柴的状态。
首先，只有一个终点，(\(0,0,0\))，为 \(P\) 位置。因为可以拿走一堆中任意根数的火柴，所以 \((x,0,0)，(0,x,0)，(0,0,x) (x>0)\) 为 \(N\) 位置。但是推广到 \((x,y,0)\) ，也就是有 \(2\) 堆火柴不为空的时候，还勉强可以计算，但到了\((x,y,z)\) ，我们会发现推导起来无比纠结。所以，我们这里要引入另外一个东西。

Nim 和

首先，我们定义 Nim和 为两个数或多个数在二进制下的异或和(异或和部分不作展开介绍，请不懂的读者自行找资料)。我们定义 “\(⊕\)” 为Nim和的运算符号。例如，如果 \(x\) 与 \(y\) 的 Nim和 是z，那么我们表示为 \(x⊕y=z\) 。

然后，引入波顿定理。

波顿定理：对 \(n\) 堆火柴 (\(x_1,x_2,x_3,...,x_n\) )，若 \(x_1⊕x_2⊕...⊕x_n = 0\) ，则这个状态为 \(P\) 位置，否则为 \(N\) 位置。

举个例子，对于 \((x_1,x_2,x_3)=(13,12,8)\)，计算它的 Nim和：

\[13 = 1011_2 \\12=1100_2 \\\ 8=1000_2 \\--------\\ Nim - sum =1001_2=9 \]

Nim和不是0，根据波顿定理，这是一个N位置。那存在能找到移动到P位置的方法吗？

根据Nim和的定义，我们发现，只要把每一列的 \(1\) 改为偶数个数就可以了。那么我们把第一堆火柴拿掉 \(9\) 根，这样子状态变为 \((4,12,8)\) ，而它的 Nim和：

\[4 = 100_2\\ 12=1100_2\\ 8=1000_2\\ ------\\ Nim - sum = 0000_2 = 0 \]

根据波顿定理，这是一个P位置。我们还可以找到另一种方法，也就是从第二对堆的 \(12\) 根火柴中拿掉 \(7\) 根，剩下 \(5\) 根，同样可以得到Nim和为0。

波顿定理的证明

波顿定理的证明参考于：Here

简单证明：

• 当 \(a\) 不全为 \(0\) 时, 任意一个 \(res!=0\) 的局面, 先手可以通过一定的操作让后手面对 \(res=0\) 的局面。
• 对于任意一个 \(res=0\) 的局面, 先手无法通过任何操作让后手面对 \(res=0\) 的局面。
• 得出结论, 当 \(res=0\) 时先手必败, 反之必胜。

详细证明：

假设现在分析 \(S(x_1,x_2,x_3,...,x_n)\) 这个状态

1. 对于终点 \((0,0,0,...,0)\)，显然 \(0⊕0⊕0⊕...⊕0=0\) ，而终点为 \(P\) 位置，成立。

2. $x_1⊕x_2⊕...⊕x_n ≠0 $

   由 \(N、P\) 位置的定义，我们知道每个 \(N\) 位置都能移动到至少一个 \(P\) 位置。下面我们来研究如何构造这样一个移动。类似上面两图的计算，我们将 Nim和看成一个竖的加法。我们找到第一列有奇数个“1”的那一列，并把任意在这一列上的“1”换成0，然后在这个数后面继续找，发现某一列的“1”的个数为奇数时，我们只要把这一列的数取反就好，即“1”变“0”，“0”变“1”。这样得出来的这个数，就是你要拿掉火柴后剩下的数。显然的，这样的一个数是肯定找得到的。也就是说，可以从该位置找到至少一个达到Nim和为0的方法，符合N位置的性质。

3. $x_1⊕x_2⊕...⊕x_n =0 \( 由\)N、P$位置的定义，我们知道每个 \(P\) 位置所能移动到的都是 \(N\) 位置。假设我们这时候把 \(x_1\) 上拿掉火柴，使它变成\(x_1’\) 根(\(x_1’<x_1\))。因为 \(x_1⊕x_2⊕...⊕x_n =0\) ，所以 \(x_1’⊕x_2⊕...⊕x_n ≠0\) ，也就是所能得到的都是 \(N\) 位置，符合 \(P\) 位置的性质。

反 Nim游戏

反Nim游戏是在逆规则下进行的Nim游戏，也就是最后操作的人失败。

在逆规则下，还能找到对于任意状态的必胜解法吗？一开始想觉得好像有点麻烦，但仔细想想，其实是可以比较简单地解决的。

先手胜当且仅当

1. 所有堆石子数都为1且游戏的SG值为0
2. 存在某堆石子数大于1且游戏的SG值不为0

证明：

1. 若所有堆石子数都为1且SG值为0，则共有偶数堆石子，故先手胜。

1）只有一堆石子数大于1时，我们总可以对该堆石子操作，使操作后石子堆数为奇数且所有堆得石子数均为1。 II

2）有超过一堆石子数大于1时，先手将SG值变为0即可，且总还存在某堆石子数大于1。

(摘自: http://hzwer.com/1950.html) 

对于反Nim游戏，其实还算比较简单的。但，是不是对于其它的游戏，它们在逆规则下也是可以这样去简单分析呢？嗯，实际上对于一些游戏是可以的，但是对大部分游戏来说，就算它们在正常规则下很容易分析，但在逆规则下会变得十分复杂，比如在后文中介绍的 Kayles and Dawson’s chess(第3章，第4部分)。

三、图论游戏

​ 在这里，我们将用有向图来表示之前所讲的几种游戏，我们用点来表示游戏中的状态，而用边来表示一个状态能到达另一个状态。接着我们会定义一个叫做 \(SG\) 函数的东西，而在第四部分中我们将介绍 \(SG\) 定理，它可以更方便我们去确定\(N、P\) 位置。

图的定义

一个有向图 \(G\)，是一对 \((X,F)\) ，其中X为一个非空点集(位置)，而 \(F\) 是表示对于任意 \(x∈X,F(x)∈X\)，表示可以将 \(x\) 移动到的位置的集合，我们称 \(F(x)\) 为 \(x\) 的后继。显然，如果 \(F(x)\) 为空集，那么 \(x\) 为终点。

游戏规则

两个人在 \(G=(X,F)\) 的图上进行图论游戏，以 \(x_0\) 为起点，双方轮流操作。在位置 \(x\) ，操作者可以将 \(x\) 移动到任意\(x_t∈F(x)\) 。移动到终点的人为胜利者。如果按着这个规则，可能会出现这个图论游戏可以无限制地进行的可能，所以《Game Theory》中给出如下定义：

To avoid this possibility and a few other problems, we first restrict attention to graphs that have the property that no matter what starting point x0 is used, there is a number n, possibly depending on x0, such that every path from x0 has length less than or equal to n. (A path is a sequence \(x_0, x_1, x_2,...,x_m\) such that \(x_i ∈ F(x_{i−1})\) for all \(i = 1,...,m\), where m is the length of the path.) Such graphs are called progressively bounded. If X itself is finite, this merely means that there are no cycles. (A cycle is a path, \(x_0, x_1,...,x_m\), with \(x_0 = x_m\) and distinct vertices \(x_0, x_1,...,x_{m−1}, m ≥ 3\))

这里就是给出了一个图的限制：图的大小无限，但是从图上任意一个点，一定存在一个正整数 \(n\)，使从该点开始到终点的所有路径长度都不大于 \(n\)。

游戏分析

为了方便讲解，我们拿第一部分中的 \(S=\{1,2,3\}\) 的减法游戏进行分析。剩余的火柴数为点，那么 \(n\) 就是起点。因为 \(0\) 终点，没有后继，所以 \(F(0)=\) ∅ 。同样的，我们会得到 \(F(1) = \{0\}，F(2) = \{0,1\}\)，并且对于 \(2 ≤ k ≤ n, F(k) = \{k−3, k−2, k−1\}\) 。对于10根火柴的情况，我们可以得到下图。

SG 函数 （The Sprague-Grundy Function）

定义：\(g(x) = min\{n \ge 0: n \not = g(y) | y \in F(x)\}\)

用文字来表示，就是不存在于x的所有后继的SG函数值(后简称SG值)中的最小值。比如：\(F(4)=\{1,2,3\}，g(1)=0,g(2)=1,g(3)=4\)，那么 \(g(4)=3\)。再比如同样的\(F(4)，g(1)=1,g(2)=2,g(3)=3\), 那么 \(g(4)=0\)。
我们将定义中的式子简写为：

\[g(x) = mex\{g(y) : y ∈ F(x)\}  \]

我们会发现，求某个 \(x\)，必须递归地去求出来，所以一般是用递推实现的。显然， F(0)=∅，所以 \(g(0)=0\)，而对于所有后继只有终点的，\(g(x)=1\)。我们后面将用这样的方式进行推导得出 \(SG\) 值。
如果我们知道了\(SG\)值，对一个图论游戏的分析便变得很简单了。如果 \(g(x)=0\) ，显然这是个P位置，如果 \(g(x)≠0\)，显然这是个 \(N\) 位置。说明如下：

1. 如果x为终点，没有后继，\(g(0)=0\)
2. \(g(x)=0\)时，因为 \(g(x)=0\)，所以对于所有 \(y∈F(x) ，g(y)≠0\) ，也就是到达的都是N位置。
3. \(g(x)≠0\)时，必然存在 \(y∈F(x) ，g(y)=0\)，即可以到达一个P位置。

当然，SG函数值肯定包含不只这些信息，更多的应用我们将在第四部分的SG定理中看到，它可以解决多个图同时存在的图论游戏的问题。

例子

我们将用下图来介绍 \(SG\) 函数的推导过程。其实很简单，如定义中一样，只要找到一个点的所有后继，然后找到不在它们后继的 \(SG\) 值之中的值即可。在图中，我们可以发现有4个终点，位于图的左侧和底部，这四个点的SG值就为0。接着我们会发现只有1个点的后继已经全部确定了，就是a点，它的SG值为1。现在b和c的后继的SG值也已全部确定，所以b,c的SG值分别确定出来。这样不断重复这个过程，知道将整张图的SG值都确定下来。

对于之前提到的 \(S=\{1,2,3\}\) 的减法游戏，它对应的SG函数是怎样的呢？终点 \(0\)，\(g(0)=0\)。状态1只能移动到终点 \(0\)，所以 \(g(1)=1\) 。状态2可以移动到 \(0,1\) ，所以 \(g(2)=2\) 。同理得到 \(g(3)=3\) 。对于状态4，它能移动到 \(1,2,3\) ,分别对应\(g(x)=\{1,2,3\}\)，所以 \(g(4)=0\)。继续重复下去，我们会得到：

观察后发现，\(g(x)=0\) 当且仅当 \(x\ mod\ 4=0\)
下面提到一种叫做至少拿一半的游戏。同样是火柴堆，但是每次你至少要拿走一半。和上面一样，我们会得出它的SG函数：

观察后，会发现 \(g(x)=min\{k|2k > x\}\)
然后仔细一想，是不是脑子进水了才去算SG值，至少拿一半，我全部拿掉不就得了...但是，在下一部分中我们会发现计算SG值是很有必要的，配合这 Nim和 来使用，可以很方便地处理多堆火柴的情况。

四、组合游戏的和

定义

给定多个组合游戏，那么你可以将这几个组合游戏合成一个新的游戏。游戏规则如下：

1. 每个游戏给定一个初始状态。
2. 双方轮流操作
3. 对于一次操作，参与者可以对其中一个组合游戏进行符合这个游戏的规则的合法操作，而其他游戏保持原状态。
4. 游戏进行直至所有组合游戏都到达终点状态，即操作者无法继续进行为止。
5. 最后一名操作者获胜。

图论游戏的和

​ 假定我们有多个满足第三部分中限制的图 \(G_1=(X_1,F_1),G_2=(X_2,F_2),...,G_n=(X_n,F_n)\) 。我们可以把这多个图组成一个新的游戏 \(G=(X,F)\),称之为图 \(G_1,G_2,...,G_n\) 的和，表示为 \(G=G_1+G_2+...+G_n\)。点集X是多个点集的笛卡尔乘积，\(X=X_1*X_2*...*X_n\)，即集合中的点为 \(\{x_1,x_2,...,x_n\}\) ,其中对于任意 \(i∈[1,n], x_i∈X_i\) 。同时对于一个点，其后继 \(F(x)\) 定义为

​ 因此，从 \(x=\{x_1,x_2,...,x_n\}\) 开始的一步移动，就是将其中任意一个 \(x_i\) 移向 \(F(x_i)\)。这样的游戏成为图论游戏的和。
​ 如果每个子游戏都满足第三部分中对图的限制，那么所得到的母游戏也符合那个限制。其移动步数的最大值显然就是所有子游戏移动步数最大值的和。

SG 定理

接下来介绍的 \(SG\) 可以很方便地求出对于图论游戏的和中的 \(SG\)值。这需要用到之前所提到的Nim和。
\(SG\) 定理：母游戏的SG值等于其各个子游戏的SG值的Nim和。

应用

SG定理在大多数组合游戏的和中可以用于求出其SG函数值，而更多的时候，我们是通过SG定理暴力求出SG函数值之后去寻找规律，减少麻烦。在《Game Theory》中有讲到很多实用的例子，作者由于时间以及能力问题暂未能够完全理解，在此不进行展开阐述。 请感兴趣的读者自行阅读《Game Theory》\(4.3\)~\(4.4\)，\(5.1\)~\(5.4\) 。

第五部分来自 OI wiki 和 Coco_T

五、树上删边游戏

游戏规则

​ 从某一棵树上删除一条边，同时删去所有在删除边后不再与根相连的部分。双方轮流进行，无法再进行删除者判定为失败，也就是比你拿掉最后一部分你就赢了。一个游戏中有多棵树，我们把它们的根都挂在天花板上…或者说，放在地板上也行..这么做是为了方便后面的一些解释和处理。

​ 在这篇文章中，我们讨论的将是公平游戏，也就是双方可以删除任意的边，我们称这个游戏为：Green Hackenbush，暂且称之为树上公平删边游戏。这个命名是因为还有另外一种删边游戏，为不公平的，参与者双方一方只能删除蓝色边，一方只能删除红色边，而绿色边是两边都可以删除的。

竹子竹子！

为了更好地解决树上删边游戏的相关问题，我们引入“竹子”。竹子长的像下面这样

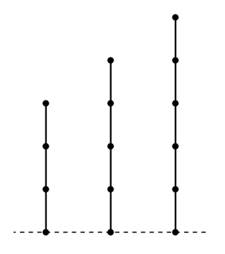
	根据上面的游戏规则，拿掉竹子上的某一节，那么竹子上面的那些也会跟着被删掉。仔细想想会发现，这不就是最简单的Nim游戏吗？有很多堆火柴，每次只能拿走某一堆火柴中的任意数量的火柴。而这里则是有很多个种在地板上的竹子，我们每次只能选一根出来，任意砍掉一部分或者全部。既然发现这是Nim游戏了，那么相应的SG值就知道了: g(x)=x..

克朗原理

	搞定竹子之后，我们就可以来研究树上删边游戏究竟要怎么解决。其实，树上删边游戏就是个披了层树皮的Nim游戏。为什么这么说呢，我们介绍克朗原理

克朗原理：对于树上某一个点，它的分支可以转换为以这个点为根的一根竹子，这个竹子的长度等于它各个分支的边的数量的异或和。

（怕翻译不好所以把原文放上来：When branches come together at a vertex, one may replace the branches by a non-branching stalk of length equal to their nim sum.）

现在我们来分析下图所示的树上删边游戏。

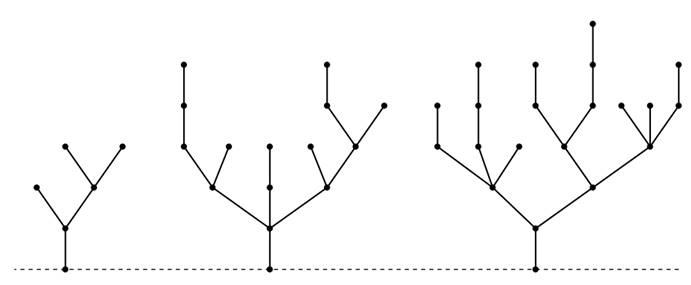
​ 对于第一个图，1号点有2个分支，分支上的边树分别为1、1，异或和为0，所以1号点的分支被替换为长度为0的竹子，也就是说上面两个分支被删掉了。所以对于2号点，就剩下2个分支，同理被消掉。最后这个图被转化为一根长度为1的竹子，其SG值为1。

	 对于第二个图，分析过程如下，SG值=8

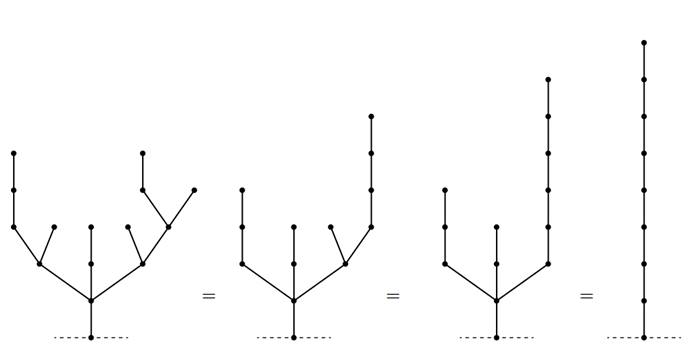
​ 对于最后一个图，同理可以得出 \(SG\) 值=4。

​ 现在，我们就可以算出这个游戏在当前状态的SG值：\(1\) xor \(8\) xor \(4=13 ≠0\)，所以这个是先手必胜状态，也就是N位置。然后剩下的就是找要到删去哪条边了。

​ 假设我们要删掉的是图3.1中第二棵树上的某一条边，也就是说，我们要让这棵树的SG值变为 1 xor 4=5，才能使得到的游戏状态的SG值为0.

​ 我们看图3.2中的倒数第二个图，这里面所得到的竹子长度： 3 xor 2 xor 6=7，我们要让它变成4，这样子加上最下面那条边的话得出来就是5. 因为 2 xor 6=4，所以可以直接删掉最左边的3条边。当然，如果要删除中间的话，那么删除的条数就是 2-4 xor 3 xor 6=1,同理，删除最右边的话，就要删去 6-4 xor 3 xor 2=1条。

​ 好了，这样子我们就利用克朗原理解决了树上删边游戏的问题。关于克朗原理的证明，因为笔者比较懒所以就不翻译过来了。请看下面这段：

Proof of the Colon Principle. Consider a fixed but arbitrary graph, G, and select an arbitrary vertex, x, in G. Let H1 and H2 be arbitrary trees (or graphs) that have the same Sprague-Grundy value. Consider the two graphs G1 = Gx : H1 and G2 = Gx : H2, where Gx : Hi represents the graph constructed by attaching the tree Hi to the vertex x of the graph G. The colon principle states that the two graphs G1 and G2 have the same Sprague-Grundy value. Consider the sum of the two games as in Figure 6.4(下图).

The claim that G1 and G2 have the same Sprague-Grundy value is equivalent to the claim that the sum of the two games has Sprague-Grundy value 0. In other words, we are to show that the sum G1 +G2 is a P-position. (证明两个游戏的SG值相同，只要证明它们的SG值异或后为0即可，也就是看成一个Nim游戏的和来理解)

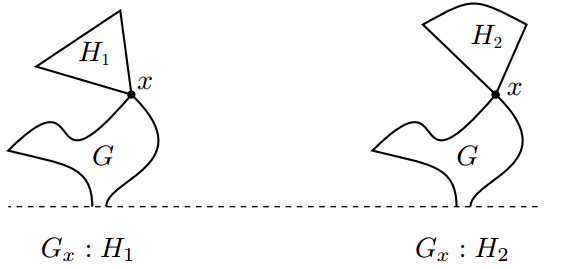
Here is a strategy that guarantees you a win if you are the second player to move in G1 + G2. If the first player moves by chopping one of the edges in G in one of the games, then you chop the same edge in G in the other game. (Such a pair of moves may delete H1 and H2 from the games, but otherwise H1 and H2 are not disturbed.) If the first player moves by chopping an edge in H1 or H2, then the Sprague-Grundy values of H1 and H2 are no longer equal, so that there exists a move in H1 or H2 that keeps the Sprague-Grundy values the same. In this way you will always have a reply to every move the opponent may make. This means you will make the last move and so win.(其实就是轮流取，慢拿的肯定赢，因为每次都可以拿走和被取走那部分SG值相同的。)

​ 其实克朗原理的意思应该这么理解，对树上一个点，在它的分支都被转换成竹子之后，我们可以求出它的SG值，而克朗原理是说，可以将它替换称一个SG值相同的竹子。其实，不单单对于树上删边游戏，应该是对于博弈论大部分问题，只要SG值相同，都可以相互转换。上面的证明是证明可以转换的原因。

图上删边游戏

研究过树上的，现在来讨论下图上删边游戏的。就像下面这样的图：

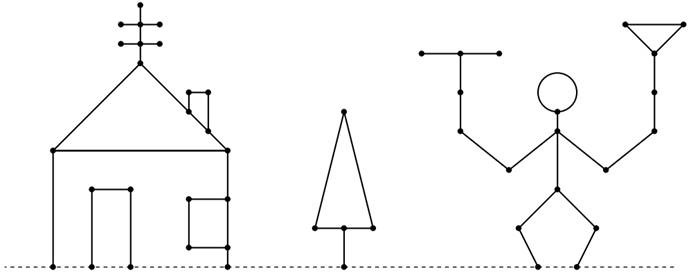
在《Game Theory》的第四章中，我们知道任意一个图都可以等价为一个Nim游戏中的火柴堆(Nim堆)。为了找到这个火柴堆，我们需要试着把这个图转换成一棵树，然后就可以用上面的办法转换成一个Nim堆。这里我们介绍另一个原理，费森原理。

费森原理：环上的点可以在被融合，且不改变图的 SG 值。

（原文：The vertices on any circuit may be fused without changing the Sprague-Grundy value of the graph.）

其实这个原理看起来好像没什么用，但是，这个原理使我们能将一个图去化简成为我们能够计算的样子。现在我们看看在图4.1是怎么化简的。

首先，我们先研究下最左边那个房子的门。如图4.2所示，地板上的那两个点可以看成一个，因为地板其实就是一个点，那么门就变成了地板上的一个三角形。接着，就用到费森原理了。三角形是一个环，而我们可以把环上的点换成连在一个点上的三个环。其实这里可以看出，费森原理是允许我们将环上的点换成一个环去表示。最后，每个环分别等价于一个大小为1的Nim堆，所以这三个环的异或和(Nim sum，后称为Nim和)是1，等价于一个大小为1的 Nim堆。

一般来说，我们可以把一个带有奇数边的环等价于只有一个端点的一条边，而偶数边的环等价于一个点。举个例子，图4.1中第二个图，树上的环带有4条边，等价于一个点，所以这棵树就被等价为一条边，即等价于一个大小为1的Nim堆。同样的，图4.1中的房子上的烟囱可以等价为一个点，右边的窗也可以等价为一个点。接着，如图4.3进行转换，我们会得到房子的SG值为3。

下面，请自己尝试计算图4.1最右边的人的SG值，答案为4。然后，试试看你能不能找到图4.1为状态的游戏的解法。

练习

《Game Theory》给的练习真的是太逗了。

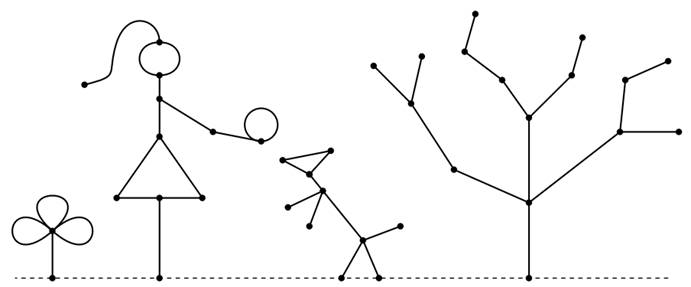
答案（从右到左）: 2 4 2 5