Codeforces Round #723 (Div. 2) （A~C题题解）

补题链接：Here

1526A. Mean Inequality

给定 $2\ast n$ 个整数序列 $a$，请按下列两个条件输出序列

• $b$ 序列是 $a$ 序列的重排序
• $b_i\ne \frac{b_{i-1}+b_{i+1}}{2}\in [1,2n]$

---

排序，然后一左一右相应输出即可

void solve() {
    int n; cin >> n;
    vector<int>v(n * 2);
    for (int &x : v)cin >> x;
    sort(v.begin(), v.end());
    int i = 0, j = 2 * n - 1;
    while (i < j) {
        cout << v[i] << " " << v[j] << " ";
        i++, j--;
    }
    cout << "\n";
}

1526B. I Hate 1111

给定正整数 $x(1\le x\le 1e9)$ 请问 $x$ 是否能被 $11,111,1111,....$ 构成？

如：

• $33=11+11+11$
• $144=111+11+11+11$

---

利用数学可证明 $1111$ 以上的数字一定能由 $11,111$ 构成，

如：$1111=11\ast 101$ 往上递推，所以我们只需要使用 $11,111$ 即可

对于 $5000$ 以下的数字，完全背包判断即可

void solve() {
    int n; cin >> n;
    for (int i = 0; i <= 20; ++i) {
        if (n % 11 == 0) {
            cout << "YES\n";
            return ;
        }
        n -= 111;
        if (n < 0)break;
    }
    cout << "NO\n";
}

1526C2. Potions (Hard Version) (反悔贪心！！！)

给定 $n(1\le n\le 2e5)$ 个药水，每个药水可回复和减少 $a_i(-{10}^9\le a_i\le {10}^9)$ 点 HP，

初始HP = 0，请问在喝药水保证 $HP>=0$ 的情况下最多能喝多少瓶药水

---

反悔贪心！！！

2.png

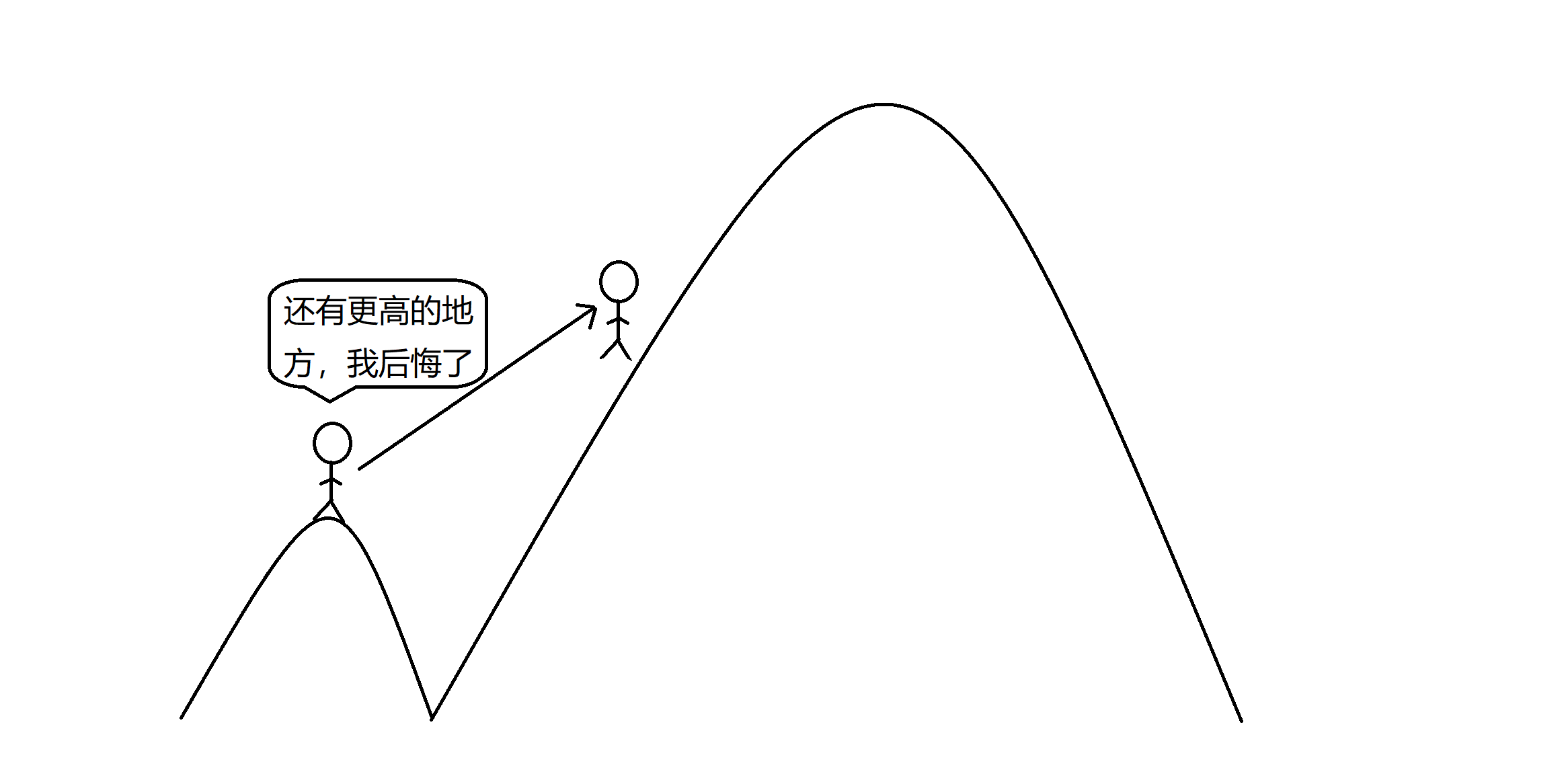
上面这张图即是最好的说明

using ll = long long;
void solve() {
    int n; cin >> n;
    priority_queue<ll, vector<ll>, greater<ll>>q;
    ll s = 0;
    for (int i = 1; i <= n; ++i) {
        ll x; cin >> x;
        s += x;
        q.push(x);
        while (s < 0) {
            s -= q.top();
            q.pop();
        }
    }
    cout << q.size();
}