2018年第九届 蓝桥杯C组 C/C++决赛题解
蓝桥杯历年国赛真题汇总：Here
1.年龄问题
s夫人一向很神秘。这会儿有人问起她的年龄，她想了想说：
"20年前，我丈夫的年龄刚好是我的2倍，而现在他的年龄刚好是我的1.5倍"。
你能算出s夫人现在的年龄吗？
注意，需要提交的是一个整数，不要填写任何多余的内容。
答案：40
2.最大乘积
把 1~9 这9个数字分成两组，中间插入乘号，
有的时候，它们的乘积也只包含1~9这9个数字，而且每个数字只出现1次。
比如：
984672 * 351 = 345619872
98751 * 3462 = 341875962
9 * 87146325 = 784316925
...
符合这种规律的算式还有很多，请你计算在所有这些算式中，乘积最大是多少？
注意，需要提交的是一个整数，表示那个最大的积，不要填写任何多余的内容。
（只提交乘积，不要提交整个算式）
答案：839542176
using ll = long long;
ll num[9], f[10], maxn, num1, num2, s;
void solve() {
for (ll i = 1; i < 10; i++) num[i - 1] = i;
maxn = 0;
do {
for (ll i = 1; i < 9; i++) {
num1 = 0;
for (ll j = 0; j < i; j++)
num1 = num1 * 10 + num[j];
num2 = 0;
for (ll j = i; j < 9; j++)
num2 = num2 * 10 + num[j];
s = num1 * num2;
if (s < 123456789 || s > 987654321) continue;
memset(f, 0, sizeof(f));
while (s) {
f[s % 10]++;
s /= 10;
}
int sum = 0;
for (int i = 1; i <= 9; i++)
if (f[i]) sum++;
if (sum == 9) maxn = max(maxn, num1 * num2);
}
} while (next_permutation(num, num + 9));
cout << maxn << endl;
}
3.全排列
对于某个串，比如：“1234”，求它的所有全排列。
并且要求这些全排列一定要按照字母的升序排列。
对于“1234”，应该输出(一共4!=24行)：
1234
1243
1324
1342
1423
1432
2134
2143
2314
2341
2413
2431
3124
3142
3214
3241
3412
3421
4123
4132
4213
4231
4312
4321
下面是实现程序，请仔细分析程序逻辑，并填写划线部分缺少的代码。
#include <stdio.h>
#include <string.h>
//轮换前n个，再递归处理
void permu(char* data, int cur)
{
int i,j;
if(data[cur]=='\0'){
printf("%s\n", data);
return;
}
for(i=cur; data[i]; i++){
char tmp = data[i];
for(j=i-1; j>=cur; j--) data[j+1] = data[j];
data[cur] = tmp;
permu(data, cur+1);
tmp = data[cur];
___________________________________ ; //填空
data[i] = tmp;
}
}
int main()
{
char a[] = "1234";
permu(a,0);
return 0;
}
请注意：只需要填写划线部分缺少的内容，不要抄写已有的代码或符号。
答案：
4.约瑟夫环
n 个人的编号是 1~n，如果他们依编号按顺时针排成一个圆圈，从编号是1的人开始顺时针报数。
（报数是从1报起）当报到 k 的时候，这个人就退出游戏圈。下一个人重新从1开始报数。
求最后剩下的人的编号。这就是著名的约瑟夫环问题。
本题目就是已知 n，k 的情况下，求最后剩下的人的编号。
题目的输入是一行，2个空格分开的整数n, k
要求输出一个整数，表示最后剩下的人的编号。
约定：\(0 < n,k < 1e6\)
例如输入：
10 3
程序应该输出：
4
资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms
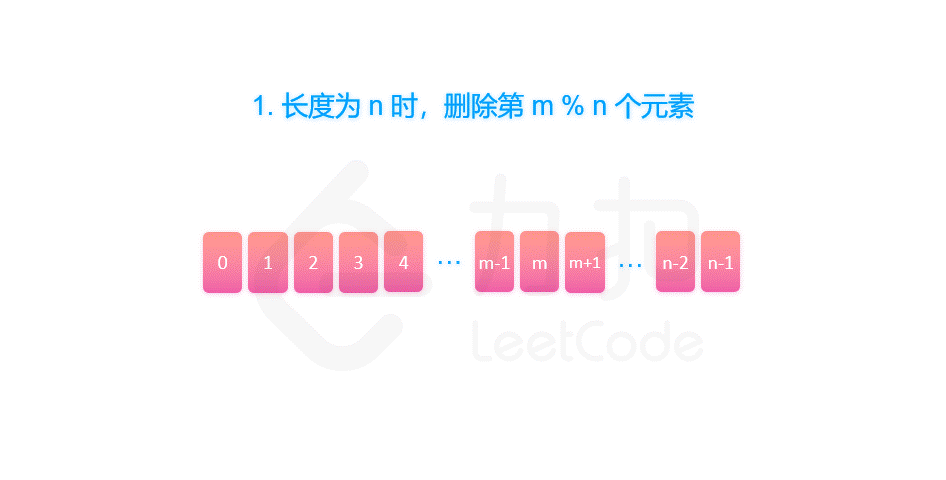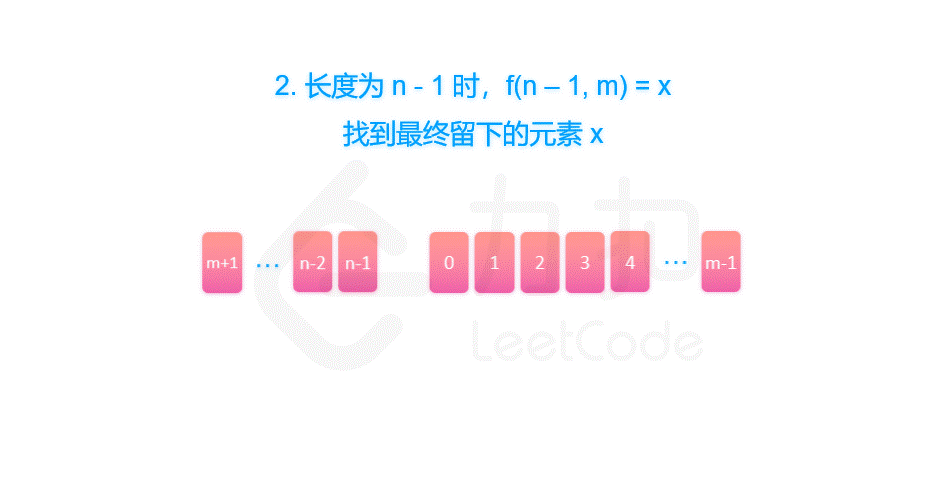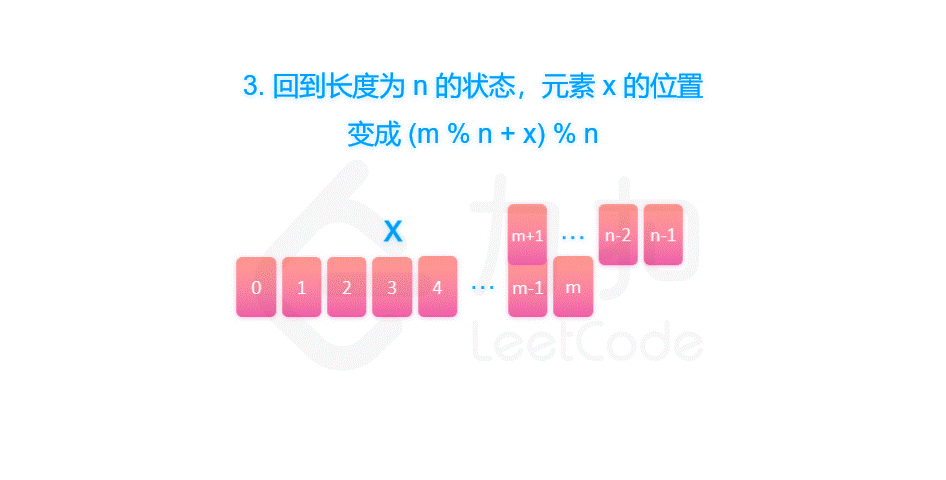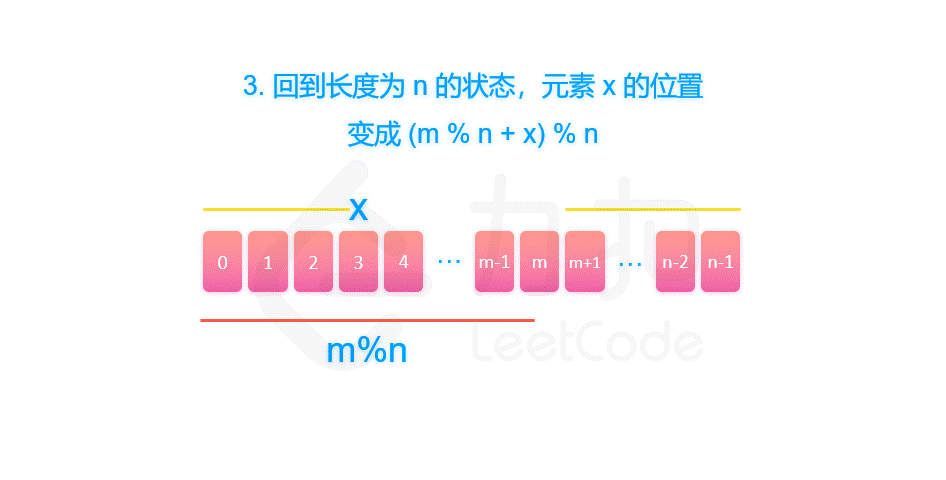
关于乔瑟夫环问题，单纯模拟在 1e6 的数据范围下肯定会 TLE
借用一下 LC 上的算法解释
int lastRemaining(int n, int m) {
int res = 0;
for (int i = 2; i <= n; i++)
res = (res + m) % i;
return res;
}
void solve() {
int n, m;
cin >> n >> m;
cout << lastRemaining(n, m) + 1 << "\n";
}
当然递归可改为递推节省堆栈空间
int lastRemaining(int n,int m){
int ans = 0;
for(int i = 2;i != n + 1;++i) ans = (ans + m) % i;
return ans;
}
5.交换次数
IT产业人才需求节节攀升。业内巨头百度、阿里巴巴、腾讯（简称BAT）在某海滩进行招聘活动。
招聘部门一字排开。由于是自由抢占席位，三大公司的席位随机交错在一起，形如：
ABABTATT，这使得应聘者十分别扭。
于是，管理部门要求招聘方进行必要的交换位置，使得每个集团的席位都挨在一起。即最后形如：
BBAAATTT 这样的形状，当然，也可能是：
AAABBTTT 等。
现在，假设每次只能交换2个席位，并且知道现在的席位分布，
你的任务是计算：要使每个集团的招聘席位都挨在一起需要至少进行多少次交换动作。
输入是一行n个字符（只含有字母B、A或T），表示现在的席位分布。
输出是一个整数，表示至少交换次数。
比如，输入：
TABTABBTTTT
程序应该输出：
3
再比如，输入：
TTAAABB
程序应该输出：
0
我们约定，输入字符串的长度n 不大于10万
资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms
【思路】
因为只有只有3个字母（B,T,A），可以考虑暴力。
3个字母有6种排列方式。对于任意一种方式进行求解，然后取出最小值即可。
例如求解的顺序是BAT，我们要先得出要放B的位置上有多少个非B的数，然后这些位置肯定是和后面的AT交换的，但是和谁交换也是有要求的，A肯定要先和在A区间上的B交换，实在没有再放到T的区间上，然后再是A和T交换。总的来说，在B区间非B的数量与B区间交换完成后在A区间非A的数量和。
const int INF = 0x3f3f3f3f;
string s;
char t[][4] = {"BAT", "BTA", "ABT", "ATB", "TBA", "TAB"};
int f(char A, char B, char C) {
int a = 0, b = 0, c = 0;
for (int i = 0; i < s.size(); i++) {
if (s[i] == A)
a++;
else if (s[i] == B)
b++;
else
c++;
}
int cia = 0, cib = 0, cic = 0, ci = 0;
for (int i = 0; i < a; i++) {
if (s[i] != A)
ci++;
if (s[i] == B)
cib++;
}
for (int i = a; i < b + a; i++) {
if (s[i] == A)
cia++;
if (s[i] == C)
cic++;
}
ci += cic + cia - min(cib, cia);
return ci;
}
void solve() {
cin >> s;
int Min = INF;
for (int i = 0; i < 6; ++i)
Min = min(Min, f(t[i][0], t[i][1], t[i][2]));
cout << Min;
}
6.迷宫与陷阱
小明在玩一款迷宫游戏，在游戏中他要控制自己的角色离开一间由NxN个格子组成的2D迷宫。
小明的起始位置在左上角，他需要到达右下角的格子才能离开迷宫。
每一步，他可以移动到上下左右相邻的格子中（前提是目标格子可以经过）。
迷宫中有些格子小明可以经过，我们用'.'表示；
有些格子是墙壁，小明不能经过，我们用'#'表示。
此外，有些格子上有陷阱，我们用'X'表示。除非小明处于无敌状态，否则不能经过。
有些格子上有无敌道具，我们用'%'表示。
当小明第一次到达该格子时，自动获得无敌状态，无敌状态会持续K步。
之后如果再次到达该格子不会获得无敌状态了。
处于无敌状态时，可以经过有陷阱的格子，但是不会拆除/毁坏陷阱，即陷阱仍会阻止没有无敌状态的角色经过。
给定迷宫，请你计算小明最少经过几步可以离开迷宫
输入
第一行包含两个整数N和K。(\(1 \le N \le 1000, 1 \le K \le 10\))
以下N行包含一个NxN的矩阵。
矩阵保证左上角和右下角是'.'。
输出
一个整数表示答案。如果小明不能离开迷宫，输出-1。
【样例输入1】
5 3
...XX
##%#.
...#.
.###.
.....
【样例输出1】
10
【样例输入2】
5 1
...XX
##%#.
...#.
.###.
.....
【样例输出2】
12
资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 3000ms
简单的BFS题，注意细节即可
const int N = 1e3 + 10;
int n, k;
char mp[N][N];
bool vis[N][N][11];
int ans;
int ax[4] = {0, 1, 0, -1};
int ay[4] = {1, 0, -1, 0};
struct node {
//结构体定义状态， x, y 为状态， k为当前剩余的无敌时间，
//s为到达这个状态的步数
int x, y, k, s;
node (int cx, int cy, int ck, int cs) {
x = cx, y = cy, k = ck, s = cs;
}
};
int bfs() {
queue<node> que;
//初始化(0, 0)点
vis[0][0][0] = true;
que.push(node(0, 0, 0, 0));
while (!que.empty()) {
//取出队头元素
node u = que.front();
que.pop();
//到达终点，返回答案
if (u.x == n - 1 && u.y == n - 1) {
return u.s;
}
//遍历上下左右四个点
for (int i = 0; i < 4; i++) {
int tx = u.x + ax[i];
int ty = u.y + ay[i];
//越界或者为墙壁，不可达
if (tx < 0 || ty < 0 || tx >= n || ty >= n || mp[tx][ty] == '#') {
continue;
}
//(tx, ty)处有一个无敌道具， 且此状态未访问过
if (mp[tx][ty] == '%' && !vis[tx][ty][k]) {
vis[tx][ty][k] = true;
que.push(node(tx, ty, k, u.s + 1));
} else {
//当前无敌，无论前方是陷阱还是道路都可走
if (u.k && !vis[tx][ty][u.k - 1]) {
vis[tx][ty][u.k - 1] = true;
que.push(node(tx, ty, u.k - 1, u.s + 1));
//当前不无敌， 而且前方为道路
} else if (mp[tx][ty] == '.' && !u.k && !vis[tx][ty][0]) {
vis[tx][ty][0] = true;
que.push(node(tx, ty, 0, u.s + 1));
}
}
}
}
//可到达的遍历完了但是仍然没有到达终点，表示不可达，返回-1
return -1;
}
int main() {
scanf("%d%d", &n, &k); //读入图的大小和无敌时间
for (int i = 0; i < n; i++) { //输入图
scanf("%s", mp[i]);
}
ans = bfs(); //调用BFS函数求解，无解时返回-1
cout << ans;
return 0;
}
