第六届蓝桥杯C++C组 A~F题题解
蓝桥杯历年国赛真题汇总:Here
1. 分机号
X老板脾气古怪,他们公司的电话分机号都是3位数,老板规定,所有号码必须是降序排列,且不能有重复的数位。比如:
751,520,321 都满足要求,而,
766,918,201 就不符合要求。
现在请你计算一下,按照这样的规定,一共有多少个可用的3位分机号码?
请直接提交该数字,不要填写任何多余的内容。
答案:120
利用 C++ STL排列组合函数
void solve() {
int ans = 0;
for (int i = 9; i >= 2; --i)
for (int j = i - 1; j >= 1; --j)
for (int k = j - 1; k >= 0; --k)if (i > j and j > k)ans++;
cout << ans;
}
2. 五星填数
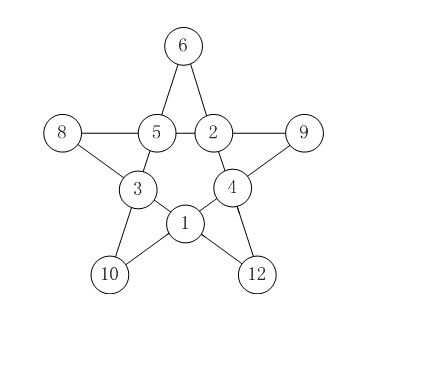
如【图1.png】的五星图案节点填上数字:1~12,除去7和11。
要求每条直线上数字和相等。
如图就是恰当的填法。
请你利用计算机搜索所有可能的填法有多少种。
注意:旋转或镜像后相同的算同一种填法。
请提交表示方案数目的整数,不要填写任何其它内容。
答案:12
给所有点都压入一维数组,然后重排序判断即可
void solve() {
int a[] = {1, 2, 3, 4, 5, 6, 8, 9, 10, 12}; // Size = 10
int ans = 0;
do {
int a1 = a[1] + a[2] + a[3] + a[4];
int a2 = a[0] + a[2] + a[5] + a[8];
int a3 = a[0] + a[3] + a[6] + a[9];
int a4 = a[1] + a[3] + a[5] + a[7];
int a5 = a[4] + a[6] + a[7] + a[9];
if (a1 == a2 and a2 == a3 and a3 == a4 and a4 == a5)ans++;
} while (next_permutation(a, a + 10));
cout << ans;
}
或者规律解法:为了满足这个题目要求,我们以1为对称
5 2
3 4
1
3 2
5 4
1
5 4
3 2
1
5 2
3 4
1
可以看到5,3在1左边的排序有4个,再算上
5,2和5,4在左边的排序
答案:\(4 * 3 = 12\)
3.二分法
二分查找法十分常用,适用于在有序的队列中搜索。
下面的程序在有序整数数组中搜索,找不到会返回-1
#include <stdio.h>
#define N 23
int find(int* m, int k)
{
int lo = 0;
int hi = N-1;
while(lo<=hi){
int mid = (lo+hi)/2;
if (k<m[mid]) hi = mid-1;
else if (k>m[mid]) lo = mid+1;
else ______________________________; //填空位置
// 答案:return mid + 1;
}
return -1;
}
int main()
{
int m[N] = {1,4,5,8,11,13,14,15,22,27,35,46,48,49,49,51,60,62,62,62,71,74,88};
printf("%d ", find(m,19));
printf("%d ", find(m,49));
printf("%d ", find(m,22));
printf("\n");
return 0;
}
请分析流程,填写划线部分缺失代码。
注意:只填写缺少的代码,不要写题面已有代码或任何其它多余内容。
答案:
return mid + 1;
4.机器人繁殖
X星系的机器人可以自动复制自己。它们用1年的时间可以复制出2个自己,然后就失去复制能力。
每年X星系都会选出1个新出生的机器人发往太空。也就是说,如果X星系原有机器人5个,
1年后总数是:5 + 9 = 14
2年后总数是:5 + 9 + 17 = 31
如果已经探测经过n年后的机器人总数s,你能算出最初有多少机器人吗?
数据格式:
输入一行两个数字n和s,用空格分开,含义如上。n不大于100,s位数不超过50位。
要求输出一行,一个整数,表示最初有机器人多少个。
例如:
用户输入:
2 31
则程序应该输出:
5
再例如:
用户输入:
97 2218388550399401452619230609499
则程序应该输出:
8
资源约定:
峰值内存消耗 < 512M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
【思路分析】
我们很容易发现,对于这一道题目,是有迹可循的,对于此我们可以简单的进行分析。
首先我们规定以下符号:
n:年数 s:机器人总数 k:最初的机器人数量
-
首先我们先看一下题目,其中我们可以发现:
那么我们将这个公式进行推广,通过数学归纳法可以得到这样的一个公式:
第n年所能产生的机器人个数 = \(2^{n}k-2^{n}+1\)
这个公式不难理解,原因也很简单,每年新增人数如下:
我们很容易发现k前的系数是\(2^{n-1}\) 而后面的偏置就是系数-1。 -
接下来我们在推导一下机器人总数s:
我们知道机器人总数s不过就是每年新增人数之和,故:
\(s = \sum_{i=1}^n(2^{i}k-2^{i}+1)+1\\ s = (2^{n+1}-1)k-(2^{n+1}-1)+n+1\)
-
那么当这个等式出来以后,我们就可以惊奇的发现,整个题目都变成了一个三元方程,后面我们只需要把这个方程解出来即可,唯一需要注意的可能就是关于大数除法的问题了。为了方便计算,我们把等式稍微变形一下:
\(s-n-1 = (2^{n+1}-1)(k-1)\)
【AC代码】
using ll = long long;
void solve() {
int n; double s; // 原本应该用大数存储,但这里double也存的下
cin >> n >> s;
ll k = (s - n - 1) / (pow(2, n + 1) - 1) + 1;
cout << k;
}
5.穿越雷区
X星的坦克战车很奇怪,它必须交替地穿越正能量辐射区和负能量辐射区才能保持正常运转,否则将报废。
某坦克需要从A区到B区去(A,B区本身是安全区,没有正能量或负能量特征),怎样走才能路径最短?
已知的地图是一个方阵,上面用字母标出了A,B区,其它区都标了正号或负号分别表示正负能量辐射区。
例如:
A + - + -
- + - - +
- + + + -
+ - + - +
B + - + -
坦克车只能水平或垂直方向上移动到相邻的区。
数据格式要求:
输入第一行是一个整数n,表示方阵的大小, 4<=n<100
接下来是n行,每行有n个数据,可能是A,B,+,-中的某一个,中间用空格分开。
A,B都只出现一次。
要求输出一个整数,表示坦克从A区到B区的最少移动步数。
如果没有方案,则输出-1
例如:
用户输入:
5
A + - + -
- + - - +
- + + + -
+ - + - +
B + - + -
则程序应该输出:
10
资源约定:
峰值内存消耗 < 512M
CPU消耗 < 1000ms
#include<bits/stdc++.h>
using namespace std;
int Min = 99999999; //用来更新最小值
int a[101][101], book[101][101]; //book标记走过的路
int x, y, x2, y2; //(x,y)标记A的坐标、(x2,y2)标记B的坐标。
int n;//矩阵大小n*n
char s;//存储临时字符
void dfs(int x, int y, int step) {
int next[4][2] = {{0, 1}, {1, 0}, { -1, 0}, {0, -1}}; //定义方向数组
int tx, ty; //定义下一个要搜索的坐标
for (int i = 0; i <= 3;
i++) { //循环(x,y)的右下左上坐标
tx = x + next[i][0];
ty = y + next[i][1];
//超出边界即跳过本次循环执行下一次
if ( tx > n || ty > n || tx < 1 || ty < 1)
continue;
if (tx == x2
&& ty == y2) { //这里之所以把满足条件更新Min放在循环内是因为下面的B点没有办法被搜素到,所以用下一个将要搜索的点来判断,step+1也是因为B点没有被dfs所以要加1.
if (step + 1 < Min)
Min = step + 1;
return;
}
int p;
p = a[x][y];
p = 0 - p; //这个p就是本题的重点了,(p==0 && step==0)就是特判从A点进入辐射区。然后就是如果搜索到了B点该怎么办?我们知道B点的状态是a[tx][ty]=0,B点的0肯定和辐射区的1、-1不相等,所以B点不能进入dfs。
if ((a[tx][ty] == p && book[tx][ty] == 0) || (p == 0 && step == 0)) {
book[tx][ty] = 1; //标记走过的点
dfs(tx, ty, step + 1);
book[tx][ty] = 0; //一次深搜结束后取消标记
}
}
return;//回溯,如果到这个点上下左右都不能走,回到上一个点。
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
cin >> s;
if (s == '+')
a[i][j] = 1;
if (s == '-')
a[i][j] = -1;
if (s == 'A') {
x = i; y = j;
}
if (s == 'B') {
x2 = i; y2 = j;
}
}
//处理矩阵并且标记A、B坐标。
dfs(x, y, 0); //从A的坐标开始搜索。
if (Min == 99999999) {
cout << -1;
} else
cout << Min;
return 0;
}
6.切开字符串
Pear有一个字符串,不过他希望把它切成两段。
这是一个长度为N(<=10^5)的字符串。
Pear希望选择一个位置,把字符串不重复不遗漏地切成两段,长度分别是t和N-t(这两段都必须非空)。
Pear用如下方式评估切割的方案:
定义“正回文子串”为:长度为奇数的回文子串。
设切成的两段字符串中,前一段中有A个不相同的正回文子串,后一段中有B个不相同的非正回文子串,则该方案的得分为A*B。
注意,后一段中的B表示的是:“...非正回文...”,而不是: “...正回文...”。
那么所有的切割方案中,A*B的最大值是多少呢?
【输入数据】
输入第一行一个正整数N(<= \(10^5\) )
接下来一行一个字符串,长度为N。该字符串仅包含小写英文字母。
【输出数据】
一行一个正整数,表示所求的A*B的最大值。
【样例输入】
10
bbaaabcaba
【样例输出】
38
【数据范围】
对于20%的数据,N<=100
对于40%的数据,N<=1000
对于100%的数据,N<=10^5
资源约定:
峰值内存消耗 < 512M
CPU消耗 < 1000ms
解题思路:
1.先枚举前后串的分割情况,每枚举出一种情况就分别对前串和后串进行处理
2.处理过程:计算前串的子串正回文个数,计算后串的子串不是正回文的个数
(注意:后串的子串只要不符合正回文都算一种情况,即它可以是非回文,可以是偶数长度回文。处理的时候我们只需要用一个check函数检测是不是正回文,前串统计返回值是1的情况,后串统计返回值是0的情况)
一开始我被误导了,以为后串的“非正回文子串”是偶数长度的回文子串
3.每处理完一种分割情况就尝试能否更新最大值
注意事项:题目要求计算的是不相同的子串,可以用一个map来查重
int n, A, B, max_ans = -1;
string s, a, b;
int check(string
str) { //用于检测字符串是否是正回文子串
if (str.length() % 2 == 0) { //如果长度是奇数,直接判错
return 0;
}
for (int i = 0; i < str.length() / 2;
i++) { //如果不是回文,直接判错
if (str[i] != str[str.length() - 1 - i])
return 0;
}
return 1;
}
int f_front(string ss) {
map<string, int> mp; //用于标记字符串是否出现过
int ans = 0;
string temp;
for (int i = 0; i < ss.length(); i++) { //枚举子串起点
for (int j = 1; j <= ss.length(); j++) { //枚举子串长度
temp = ss.substr(i, j);
if (check(temp)
&& !mp.count(
temp)) { //如果这个串是正回文并且没有出现过
mp[temp] = 1;
ans++;
}
}
}
return ans;
}
int f_rear(string ss) {
map<string, int> mp; //用于标记字符串是否出现过
int ans = 0;
string temp;
for (int i = 0; i < ss.length(); i++) { //枚举子串起点
for (int j = 1; j <= ss.length(); j++) { //枚举子串长度
temp = ss.substr(i, j);
if (!check(temp)
&& !mp.count(
temp)) { //如果这个串不是正回文并且没有出现过
mp[temp] = 1;
ans++;
}
}
}
return ans;
}
void sovle() {
cin >> n >> s;
for (int i = 1; i <= s.length() - 1; i++) { //枚举前串的长度
a = s.substr(0, i); //前串,起点是0,长度是i
b = s.substr(i, s.length() -
i); //后串,起点是i,长度是length-i
//cout << "前串:"+a << endl <<"后串:"+ b <<endl;
A = f_front(a);
B = f_rear(b);
if (A * B > max_ans) {
max_ans = A * B;
}
}
cout << max_ans << endl;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号