2019年第十届蓝桥杯国赛C++B组
部分题目示意图来自网络，所以会带水印
最后编辑时间：
2021年5月12日
统一声明
如果不写默认带有常用头文件
如果不表明主函数默认表示在 void solve(){}
默认使用
using namespace std;
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using ll = long long;
填空题答案速览
- 7020
- 55965365465060
- 2444 不知道对不对
- 45360
A-平方序列：
题意: 求 \(2019<X<Y\) ,使 \(2019*2019,X*X,Y*Y\) 组成等差数列且 \(X+Y\) 最小
利用等差数列性质：\(a_0 + a_2 = 2 * a_1\) 跑一遍即可
using ll = long long;
void solve() {
ll w = 2019 * 2019, x, y;
for (int i = 2020; i <= 10000; ++i) {
x = i * i;
y = 2 * x - w;
if (sqrt(y) == (int)sqrt(y)) break;
}
cout << sqrt(x) + sqrt(y);
}
B-质数拆分：
把2019分成若干个素数相加，求有多少种分法。
元素完全相同的算同一种方法，比如 2+2017=2019和2017+2=2019
思路：先预处理出 2~2019中所有的素数，然后写01背包即可
// 55965365465060
using ll = long long;
int prime[] = {1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017};
void solve() {
int n = 307;
ll a[2020] = {1};
for (int i = 1; i <= 306; i++) {
for (int j = 2019; j >= prime[i]; j--)
a[j] += a[j - prime[i]];
}
printf("%lld", a[2019]);
}
写法修正
bool vis[2020];
ll dp[2020] = {1};
void solve() {
memset(vis, true, sizeof(vis));
vector<int> prime;
for (int i = 2; i <= 2020; ++i)
if (vis[i])
for (int j = i + i; j <= 2020; j += i) vis[j] = false;
for (int i = 1; i <= 2019; ++i)
if (vis[i]) prime.push_back(i);
// cout << prime.size() << "\n";
for (int i = 1; i < prime.size(); ++i)
for (int j = 2019; j >= prime[i]; --j) dp[j] += dp[j - prime[i]];
cout << dp[2019] << "\n";
}
看了一下CSDN一位dalao写的记忆化搜索，感觉写的很好，记录一下
using ll = long long;
bool vis[3040];
vector<int> prime;
ll f[3020][3020];
ll dfs(int pos, ll sum) {
if (f[pos][sum] != -1) return f[pos][sum];
if (sum == 2019) return 1;
if (pos >= prime.size() || sum > 2019) return 0;
ll ans = 0;
ans += dfs(pos + 1, sum);
ans += dfs(pos + 1, sum + prime[pos]);
return f[pos][sum] = ans;
}
void solve() {
// 素数筛
memset(vis, true, sizeof(vis));
for (int i = 2; i <= 3020; ++i) {
if (vis[i])
for (int j = i + i; j <= 3020; j += i) vis[j] = false;
}
for (int i = 2; i <= 2019; ++i)
if (vis[i]) prime.push_back(i);
memset(f, -1, sizeof(f)); // 初始化dp数组
ll ans = dfs(0, 0);
cout << ans << "\n";
}
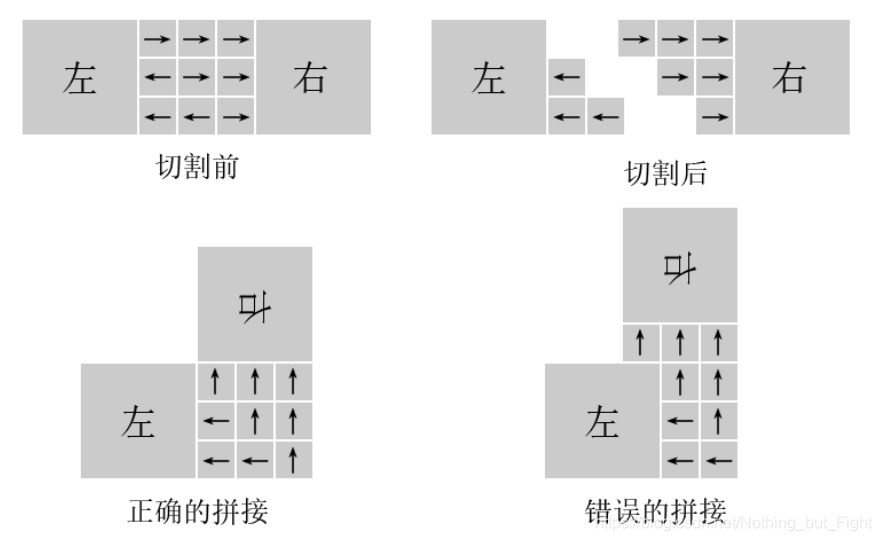
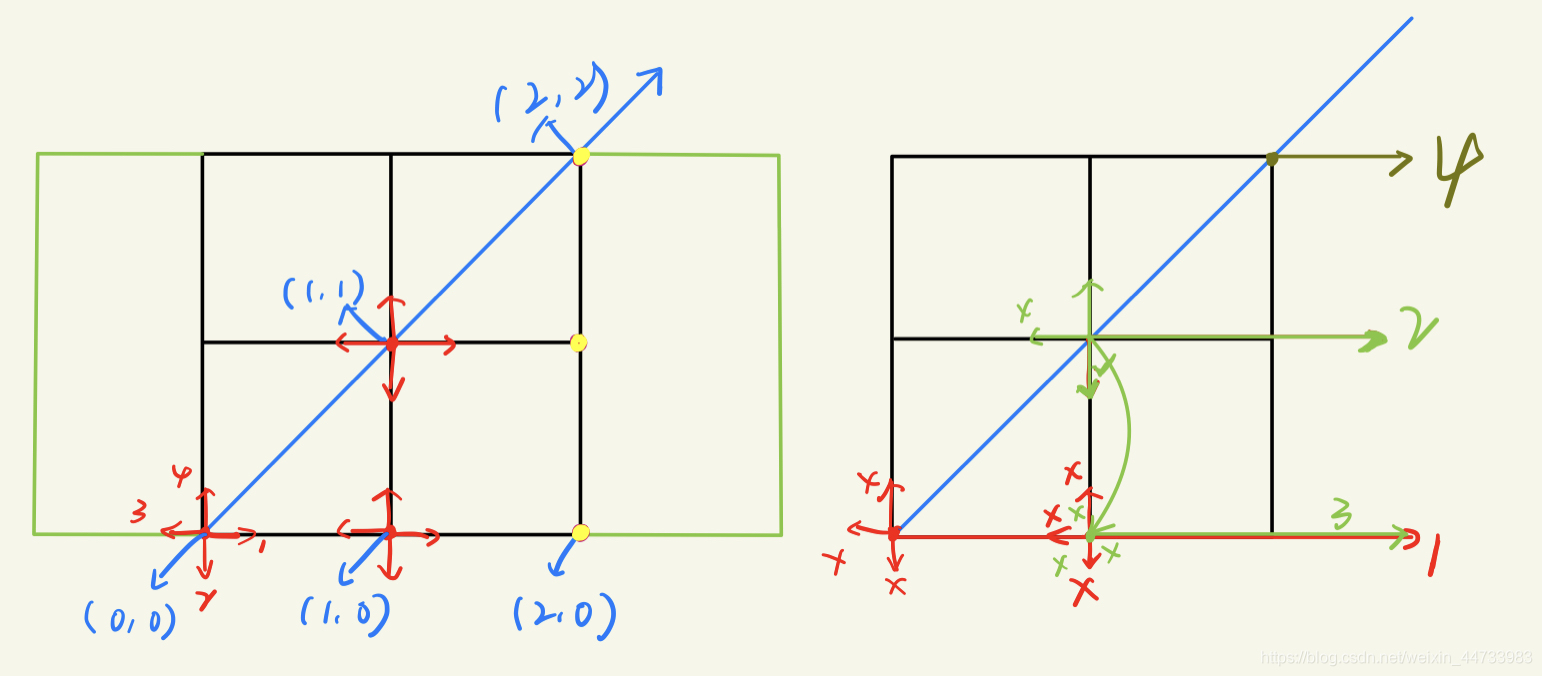
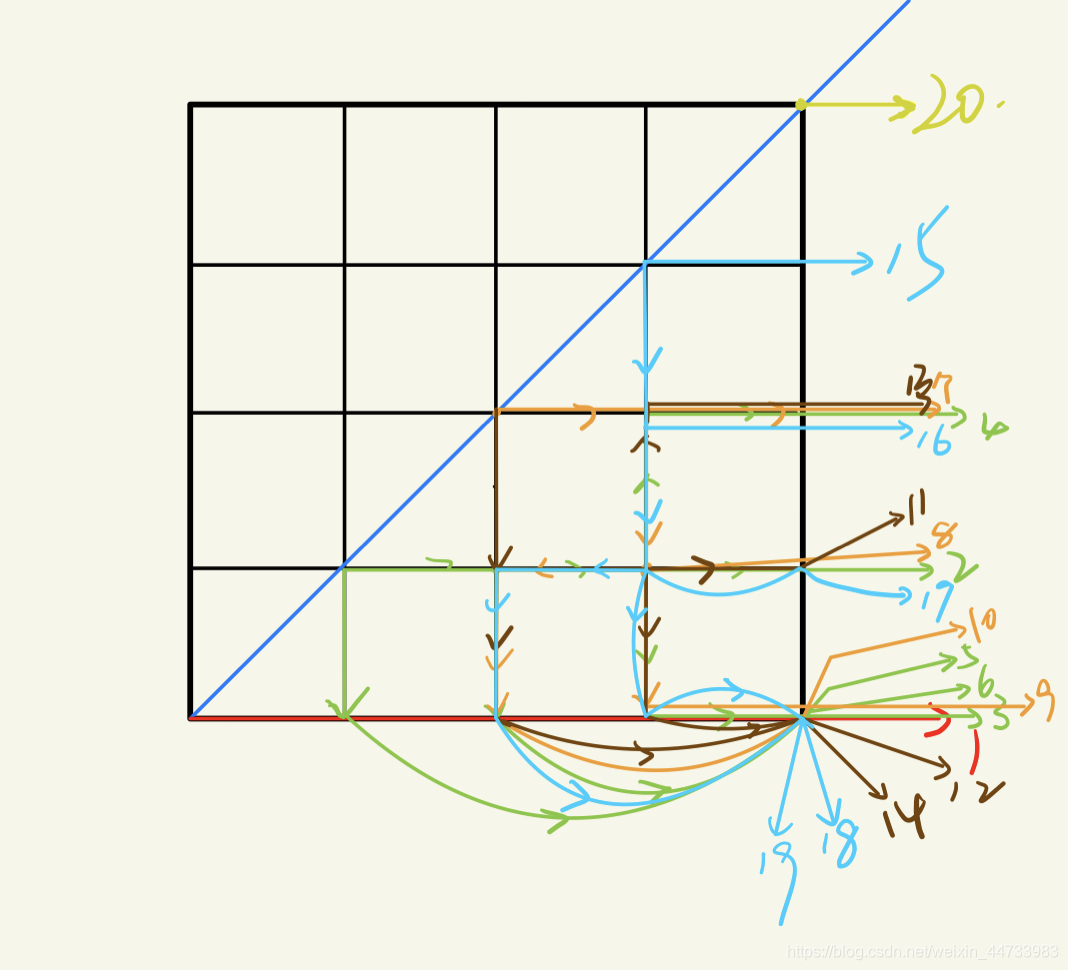
C-拼接：
小明要把一根木头切成两段，然后拼接成一个直角。如下图所示，他把中间部分分成了nXn的小正方形，他标记了每个小正方形属于左边还是右边。然后沿两边的分界线将木头切断，将右边旋转向上后拼接在一起。
要求每个小正方形都正好属于左边或右边，而且同一边的必须是连通的。在拼接时，拼接的部位必须保持在原来大正方形里面。请问，对于7的小正方形，有多少种合法的划分小正方形的方式。
思路来自 葡萄君
先以2 * 2为例
我先以左下角和右上角为轴，这样的话，右下方画出的分割线对称之后就是整体的。我发现的规律就是从这条对角线上的每个点出发，向四个方向搜索，如果条件是对的就可以到下个点继续，直到到了最右边的竖线上的任意一点，此时为一种情况，并返回。
4 * 4 和后面是同理的。
int a[8][8];
int num = 0;
int b[4][2] = {{1, 0}, {0, -1}, {-1, 0}, {0, 1}};
void tc() {
for (int i = 0; i < 8; i++)
for (int j = 0; j < 8; j++)
a[i][j] = 0;
}
void DFS(int x, int y, int bx, int by) {
a[x][y] = 1;
if (x == 7) {
//cout << x << " " << y << endl;
num++;
a[x][y] = 0;
return;
}
int tx = 0, ty = 0;
for (int i = 0; i < 4; i++) {
tx = x + b[i][0];
ty = y + b[i][1];
if ((y == 0 && (i == 2 || i == 3)) || (tx < 0 || ty < 0) || a[tx][ty] == 1) {
if (i == 3)
a[x][y] = 0;
continue;
}
if ((tx == ty || tx < ty) || (tx == bx && ty == by)) {
if (i == 3)
a[x][y] = 0;
continue;
}
else {
a[x][y] = 1;
DFS(tx, ty, x, y);
if (i == 3)
a[x][y] = 0;
continue;
}
}
}
void solve() {
for (int i = 0; i <= 7; i++) {
tc();
DFS(i, i, -2, -2);
}
cout << num;
}
只不过方格越多情况也就越多最基本的是，你在这个点搜索的时候，不能再回到你来的那方向。在最下面那条线上的时候，不能再向上搜索，等等。
D-求值：
学习了约数后，小明对于约数很好奇，他发现，给定一个正整数t，总是可以找到含有t个约数的整数。小明对于含有t个约数的最小数非常感兴趣，并把它定义为St。例如S1= 1,S2= 2,S3= 4,S4= 6，。现在小明想知道，当t= 100时，St是多少？即S100是多少？
开两重 for 循环暴力找
// 45360
void solve() {
for (int i = 1;; ++i) {
int sum = 0;
for (int j = 1; j <= i; ++j)
if (i % j == 0) sum++;
if (sum == 100) {
cout << i << "\n";
return;
}
}
}
E-路径计数：
有一个7X7的方格。方格左上角顶点坐标为(0,0)，右下角坐标为(7,7)。
求满足下列条件的路径条数：
1、起点和终点都是(0,0)
2、路径不自交
3、路径长度不大于12
4、对于每一个顶点，有上下左右四个方向可以走，但是不能越界。
206
F-最优包含：
题目给定两个字符串S和T，保证S的长度不小于T的长度，问至少修改S的多少个字符，可以令T成为S的子序列。
输入描述：
两行。
第一行是字符串S，第二行是字符串T。
保证S的长度不小于T的长度，S的长度范围在10~1000之间。
输出描述：
答案，一个非负整数。
输入样例：
XBBBBBAC
ACC
输出样例：
2
最小编辑距离--DP
dp[i][j]表示令T的前j个字符成为S的前i个字符的子序列需要修改的字符个数。
先初始化i=j和j=0的情况。
状态转移方程：if (s[i] == t[j]) dp[i][j] = dp[i - 1][j - 1]; else dp[i][j] = min(dp[i - 1][j], dp[i - 1][j - 1] + 1);
const int N = 1e3 + 10;
int dp[N][N];
string s, t;
void solve() {
cin >> s >> t;
int ls = s.size();
int lt = t.size();
if (s[0] != t[0])
dp[0][0] = 1;
for (int i = 1; i < lt; i++)
if (s[i] == t[i])
dp[i][i] = dp[i - 1][i - 1];
else
dp[i][i] = dp[i - 1][i - 1] + 1;
for (int i = 1; i < ls; i++) {
if (s[i] == t[0])
dp[i][0] = 0;
else
dp[i][0] = dp[i - 1][0];
}
// 开始编辑判断字符串距离
for (int j = 1; j < lt; j++)
for (int i = j + 1; i < ls; i++)
if (s[i] == t[j])
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min(dp[i - 1][j], dp[i - 1][j - 1] + 1);
cout << dp[ls - 1][lt - 1] << '\n';
}
G-排列数：
对于一个数列中的某个数，如果这个数比两侧的数都大或比两侧的数都小，我们称这个数为这个数列的一个转折点。
如果一个数列有t个转折点，我们称这个数列为t+1调数列。
给定两个正整数n,k。求在1~n的全排列中，有多少个数列是k调数列。
输入描述：
两个正整数n,k。
输出描述：
答案，一个整数。
输入样例：
4 2
输出样例：
12
const int N = 1e3 + 10;
int n, k, ans, a[N];
void swap(int x, int y) {
int t = a[x];
a[x] = a[y];
a[y] = t;
return;
}
bool pd(int x) { //判断a[x]是不是转折点
if (a[x] > a[x - 1] && a[x] > a[x + 1] || a[x] < a[x - 1] && a[x] < a[x + 1])
return 1;
return 0;
}
void dfs(int m, int sum) { //m为递归层数，sum为已经有的转折点数量
if (m > 2 && pd(m - 2)) //判断a[m-2]是不是转折点
sum++;
if (sum > k - 1 || sum + n - m < k - 1) //转折点过多或者过少都剪枝
return;
if (m == n - 1) { //全排列递归出口
if (m > 1 && pd(m - 1))
sum++;
if (sum == k - 1)
ans++;
return;
}
for (int i = m; i < n; i++) { //全排列函数的函数主体
swap(m, i);
dfs(m + 1, sum);
swap(m, i);
}
}
void solve() {
cin >> n >> k;
for (int i = 0; i < n; i++) a[i] = i + 1;
dfs(0, 0);
cout << ans << endl;
}
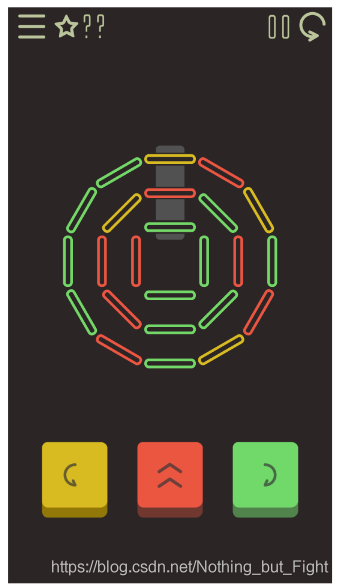
H-解谜游戏：
小明正在玩一款解谜游戏。谜题由24根塑料棒组成，其中黄色塑料棒4根，红色8根，绿色12根(后面用Y表示黄色、R表示红色、G表示绿色)。初始时这些塑料棒排成三圈，如上图所示，外圈12根，中圈8根，内圈4根。小明可以进行三种操作：
-
将三圈塑料棒都顺时针旋转一个单位。例如当前外圈从0点位置开始顺时针依次是YRYGRYGRGGGG，中圈是RGRGGRRY，内圈是GGGR。那么顺时针旋转一次之后，外圈、中圈、内圈依次变为：GYRYGRYGRGGG、YRGRGGRR和RGGG。
-
将三圈塑料棒都逆时针旋转一个单位。例如当前外圈从0点位置开始顺时针依次是YRYGRYGRGGGG，中圈是RGRGGRRY，内圈是GGGR。那么逆时针旋转一次之后，外圈、中圈、内圈依次变为：RYGRYGRGGGGY、GRGGRRYR和GGRG
-
将三圈0点位置的塑料棒做一个轮换。具体来说：外圈0点塑料棒移动到内圈0点，内圈0点移动到中圈0点，中圈0点移动到外圈0点。例如当前外圈从0点位置开始顺时针依次是YRYGRYGRGGGG，中圈是RGRGGRRY，内圈是GGGR。那么轮换一次之后，外圈、中圈、内圈依次变为：RRYGRYGRGGGG、GGRGGRRY和YGGR。小明的目标是把所有绿色移动到外圈、所有红色移动中圈、所有黄色移动到内圈。给定初始状态，请你判断小明是否可以达成目标。
输入描述：
第一行包含一个整数T，代表询问的组数。(1<T<100)。每组询问包含3行：第一行包含12个大写字母，代表外圈从0点位置开始顺时针每个塑料棒的颜色。第二行包含8个大写字母，代表中圈从0点位置开始顺时针每个塑料棒的颜色。第三行包含4个大写字母，代表内圈从0点位置开始顺时针每个塑料棒的颜色。
输出描述：
对于每组询问，输出一行YES或者NO，代表小明是否可以达成目标。
输入样例：
2
GYGGGGGGGGGG
RGRRRRRR
YRYY
YGGGRRRRGGGY
YGGGRRRR
YGGG
输出样例：
YES
NO
I-第八大奇迹：
在一条R河流域，繁衍着一个古老的名族Z。他们世代沿河而居，也在河边发展出了璀璨的文明。
Z族在R河沿岸修建了很多建筑，最近，他们热衷攀比起来。他们总是在比谁的建筑建得最奇特。
幸好Z族人对奇特的理解都差不多，他们很快给每栋建筑都打了分，这样评选谁最奇特就轻而易举了。
于是，根据分值，大家很快评出了最奇特的建筑，称为大奇迹。
后来他们又陆续评选了第二奇特、第二奇特、…、第七奇特的建筑，依次称为第二大奇迹、第三大奇迹、…、第七大奇迹。
最近，他们开始评选第八奇特的建筑，准备命名为第八大奇迹。在评选中，他们遇到了一些问题。
首先，Z族一直在发展，有的建筑被拆除又建了新的建筑，新建筑的奇特值和原建筑不一样，这使得评选不那么容易了。
其次，Z族的每个人所生活的范围可能不一样，他们见过的建筑并不是所有的建筑，他们坚持他们自己所看到的第八奇特的建筑就是第八大奇迹。
Z族首领最近很头疼这个问题，他害怕因为意见不一致导致Z族发生分歧。他找到你，他想先了解一下，民众自己认为的奇迹是怎样的。
现在告诉在R河周边的建筑的变化情况，以及在变化过程中一些人的生活范围，请编程求出每个人认为的第八大奇迹的奇特值是多少
输入描述：
输入的第一行包含两个整数L,N，分别表示河流的长度和要你处理的信息的数量。开始时河流沿岸没有建筑，或者说所有的奇特值为0。接下来N行，每行一条你要处理的信息。
如果信息为C p x，表示流域中第p个位置(1<=p<=L)建立了一个建筑，其奇特值为x。如果这个位置原来有建筑，原来的建筑会被拆除。
如果信息为Q a b，表示有个人生活的范围是河流的第a到b个位置（包含a和b，a<=b），这时你要算出这个区间的第八大奇迹的奇特值，并输出。如果找不到第八大奇迹，输出0。
输出描述：
对于每个为Q的信息，你需要输出一个整数，表示区间中第八大奇迹的奇特值。
输入样例：
10 14C 1 5C 2 4C 3 7C 4 6C 5 5C 6 1C 7 8Q 1 10C 8 3C 9 6C 10 3Q 1 9C 6 10Q 1 10
输出样例：
034
线段树+sort
J-燃烧权杖：
小C最近迷上了一款游戏。现在，在游戏中，小C有一个英雄，生命值为x；敌人也有一个英雄，生命值为y。除此以外，还有k个士兵，生命值分别为a1、a2、…、ak。
现在小C打算使用一个叫做“燃烧权杖”的技能。“燃烧权杖”会每次等概率随机选择一个活着的角色（英雄或士兵），扣减其10点生命值，然后如果该角色的生命值小于或等于0，则该角色死亡，不会再被“燃烧权杖”选中。“燃烧权杖”会重复做上述操作，直至任意一名英雄死亡。
小C想知道使用“燃烧权杖”后敌方英雄死亡（即，小C的英雄存活）的概率。为了避免精度误差，你只需要输出答案模一个质数p的结果，具体见输出格式。
输入描述：
输入包含多组数据。输入第一行包含一个正整数T，表示数据组数。接下来T组，每组数据第一行包含四个非负整数x、y、p、k，分别表示小C的英雄的生命值、敌方英雄的生命值，模数和士兵个数。第二行包含k个正整数a1、a2、…、ak，分别表示每个士兵的生命值
输出描述：
对于每组数据，输出一行一个非负整数，表示答案模质数p的余数。可以证明，答案一定为有理数。设答案为a/b（a和b为互质的正整数），你输出的数为x，则你需要保证a与bx模p同余；也即，x= (a*b-1)mod p，其中b-1表示b模p的逆元，mod为取模运算。
待补
