【算法学习笔记】斜率优化DP

学习自AcWing的一位学长的分享和《算法竞赛进阶指南》

斜率优化DP的前置知识点：求过两点的一次函数的斜率…

已知两点 \((x_1,y_1),(x_2,y_2)\) 对于待定方程：\(y = kx + b \to k = \frac{y_1 - y_2}{x_2 - x_1}\)

---

故事围绕着《算法竞赛进阶指南》的几道例题展开：

引子

任务安排 1：

假如我们启动了一个任务\([l, r]\)，那么它会对后面造成\(S * \sum_{i = r + 1}^{n} C_i\)的费用。

所以我们可以使用费用提前计算的方式优化算法：

设\(st\)为 \(t\) 的前缀和，设\(sum\)为\(C\)的前缀和

\(f[i]\) 表示安排完前 \(i\) 个任务的最小花费：

$f[i] = min(f[j] + (sum[i] - sum[j]) * t[i] + (sum[n] - sum[j]) * S) $

时间复杂度\(\mathcal O(N ^ 2)\)

情况1. 斜率、横坐标皆单调递增

任务安排 2：

将上题推出的转移式子得 \(min\) 去掉观察：

\(f[i] = f[j] + (sum[i] - sum[j]) * t[i] + (sum[n] - sum[j]) * S\)

发现我们无法优化\(dp\)的原因是有与 \(i, j\) 两者都有关的乘积项，导致我们没有最优策略：

\(- sum[j] * t[i]\)

斜率优化

考虑把这个式子拆开转换为一次函数：\(y = kx + b\) 的形式。

将与 \(i,\ j\) 都有关系的乘积项作为 \(kx\)，其中与 \(i\) 有关的作为 \(k\)，与 \(j\) 有关的作为 \(x\)

将只与 \(j\) 有关系的值作为 \(y\) ，其余的当做 \(b\)

则以上式子可以化成：

\(\underline{f[j]}_y = \underline{(t[i] + S)}_k * \underline{sum[j]}_x + \underline{f[i] - sum[i] * t[i] - sum[n] * S}_b\)

发现当 \(i\) 确定后，该一次函数的斜率 \(k\) 确定，则截距 \(b\) 越小， \(f[i]\) 越小。

我们将 \((x, y)\) 即 \((sum[j], f[j])\) 放在坐标系上。

则形象化可理解为一条直线从下往上平移，所碰到的第一个点即为最优解。

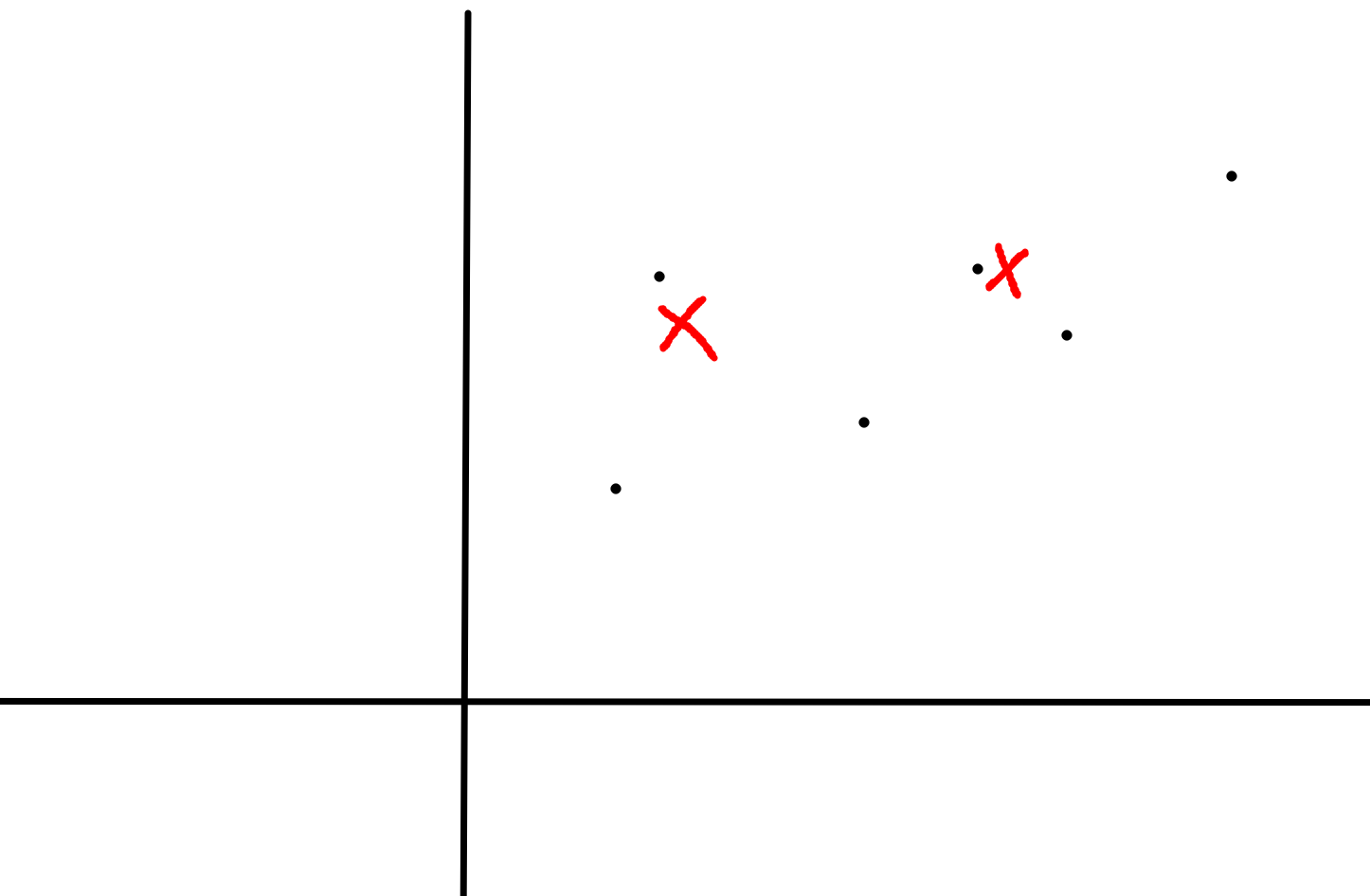
发现一个点如果被另外两个点围起来，永远不可能作为最优解。

删除了这些点后，发现相邻点之间的斜率为单调递增的，即构成一个凸包：

发现一个斜率 \(k\) 固定的直线所匹配的最优点满足：

• 其右边的斜率都 \(> k\)
• 其左边的斜率都 \(< k\)

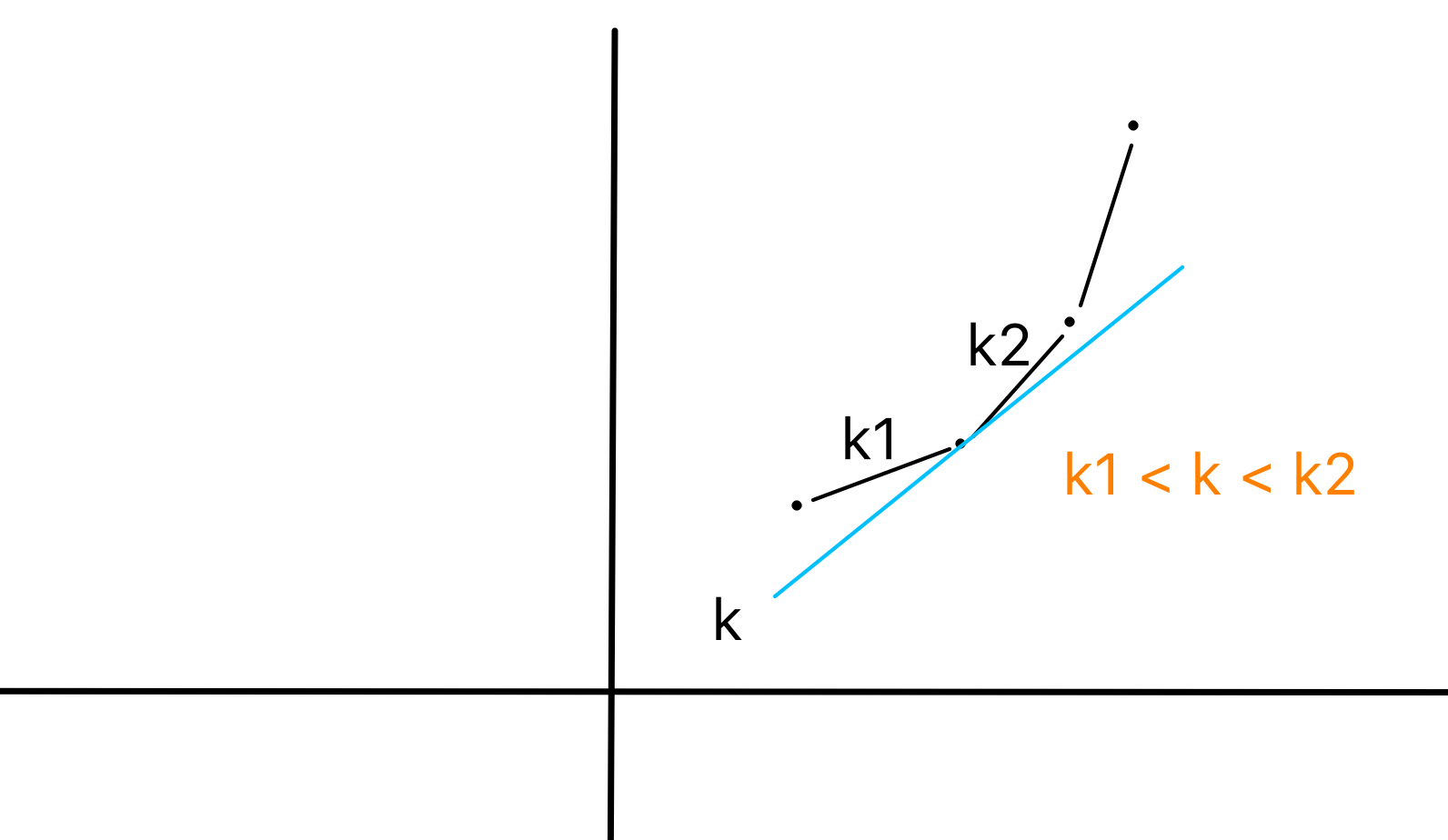
由于这道题斜率 \(t[i] + S\)、横坐标 \(sum[j]\) 皆单调递增。

1. 由于横坐标递增，所以维护凸包时，每当加入一个点时：
2. 若上面两个点构成的斜率大于这个点和上一个点的斜率，即不满足单调性，可以弹出队尾。即：$\frac{y_{i} - y_{q[tt]}}{x_{i} - x_{q[tt]}} \le \frac{y_{q[tt]} - y_{q[tt - 1]}}{x_{q[tt]} - x_{q[tt - 1]}} $
3. 由于斜率递增，所以 \(i + 1\) 的最优解一定在 \(i\) 的右边，所以一旦队头两个点构成的斜率 \(<\) 当前的斜率，可以弹出队头。即满足：\(\frac{y_{q[hh + 1]} - y_{q[hh]}}{x_{q[hh + 1]} - x_{q[hh]}} < t[i] + S\)

然后队头的元素即为最优选择。

时间复杂度 \(O(N)\)

\(Tips:\) 由于除法会有精度问题，可以通过交叉相乘的形式比较大小

#include <cstdio>
#include <cstring>
#include <iostream>
#define x(a) (c[a])
#define y(a) (f[a])
#define k(a) (t[a] + S)
using namespace std;
typedef long long LL;
const int N = 300005;
int n, S;
LL t[N], c[N], q[N], f[N];
int main() {
    scanf("%d%d", &n, &S);
    for (int i = 1; i <= n; i++) scanf("%lld%lld", t + i, c + i);
    for (int i = 1; i <= n; i++) t[i] += t[i - 1], c[i] += c[i - 1];
    int hh = 0, tt = 0;
    q[0] = 0;
    for (int i = 1; i <= n; i++) {
        while (hh < tt && (y(q[hh + 1]) - y(q[hh])) <= ((t[i] + S) * (x(q[hh + 1]) - x(q[hh])))) hh++;
        f[i] = f[q[hh]] + (c[i] - c[q[hh]]) * t[i] + (c[n] - c[q[hh]]) * S;
        while (hh < tt && ((y(q[tt]) - y(q[tt - 1])) * (x(i) - x(q[tt])) >= ((y(i) - y(q[tt])) * (x(q[tt]) - x(q[tt - 1]))))) tt--;
        q[++tt] = i;
    }
    printf("%lld\n", f[n]);
    return 0;
}

情况2. 横坐标单调递增

任务安排3

此时的斜率不再递增了，也就是我们不能\(pop_front\)了，不过我们仍可以维护凸包，然后保持单调性，二分。

时间复杂度\(O(Nlog_2N)\)

#include <cstdio>
#include <cstring>
#include <iostream>
#define x(a) (c[a])
#define y(a) (f[a])
#define k(a) (t[a] + S)
using namespace std;
typedef long long LL;
const int N = 300005;
int n, S, t[N], c[N], q[N];
LL f[N];
int main() {
    scanf("%d%d", &n, &S);
    for (int i = 1; i <= n; i++) scanf("%lld%lld", t + i, c + i);
    for (int i = 1; i <= n; i++) t[i] += t[i - 1], c[i] += c[i - 1];
    int hh = 0, tt = 0;
    q[0] = 0;
    for (int i = 1; i <= n; i++) {
        int l = hh, r = tt;
        while (l < r) {
            int mid = (l + r) >> 1;
            if ((y(q[mid + 1]) - y(q[mid])) >= ((LL)k(i) * (x(q[mid + 1]) - x(q[mid])))) r = mid;
            else
                l = mid + 1;
        }
        f[i] = f[q[r]] + (LL)(c[i] - c[q[r]]) * t[i] + (LL)(c[n] - c[q[r]]) * S;
        while (hh < tt && ((y(q[tt]) - y(q[tt - 1])) * (x(i) - x(q[tt])) >= ((y(i) - y(q[tt])) * (x(q[tt]) - x(q[tt - 1]))))) tt--;
        q[++tt] = i;
    }
    printf("%lld\n", f[n]);
    return 0;
}

例题

运输小猫

设 \(d[i]\) 为从 \(1\) 走到 \(i\) 的距离。

那么每条小猫最佳的出发时间应为 \(a[i] = t[i] - d[h[i]]\)，如果要接上这只猫，必须大于这个时间出发。

我们将 \(a\) 数组排序，那么问题等价转换于把 \(m\) 个点划分成 \(p\) 个连续区间，使每一段到右端点的距离之和的总和最小。（内心 \(OS\)：这不就是摆渡车的变种吗？）

那么朴素 \(dp\) 便很好列出了：

\(f[k][i]\) 表示将前 \(i\) 只小猫分成 \(k\) 组的最小总和。

设 \(sumA\) 为 \(a\) 数组的前缀和。

\(f[k][i] = min(f[k - 1][j] + a[i] * (i - j) - sumA[i] + sumA[j]) (0 \le j < i)\)

---

由于这里面有一个非常讨厌的 \(a[i] * -j\)，所以我们考虑斜率优化：

\(\underline{f[k - 1][j] + sumA[j]}_y = \underline{a[i]}_k * \underline{j}_x + \underline{f[k][i] - a[i] * i + sumA[i]}_b\)

发现这里的横坐标、斜率都是单调递增，即情况 \(1\)。那么我们可以将不需要的直接踢出即可。

时间复杂度 \(O(PM)\)

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 100005, S = 105;
int n, m, P, d[N], a[N], q[N];
LL f[S][N], sum[N];
LL inline y(int i, int k) {
    return f[k - 1][i] + sum[i];
}
int main() {
    memset(f, 0x3f, sizeof f);
    scanf("%d%d%d", &n, &m, &P);
    for (int i = 0; i <= P; i++) f[i][0] = 0;
    for (int i = 2; i <= n; i++)
        scanf("%d", d + i), d[i] += d[i - 1];

    for (int i = 1, h, t; i <= m; i++) {
        scanf("%d%d", &h, &t);
        a[i] = t - d[h];
    }
    sort(a + 1, a + 1 + m);
    for (int i = 1; i <= m; i++) sum[i] = sum[i - 1] + a[i];
    for (int k = 1; k <= P; k++) {
        int hh = 0, tt = 0;
        for (int i = 1; i <= m; i++) {
            while (hh < tt && (y(q[hh + 1], k) - y(q[hh], k)) <= (LL)a[i] * (q[hh + 1] - q[hh])) hh++;
            f[k][i] = f[k - 1][q[hh]] + (LL)a[i] * (i - q[hh]) - (sum[i] - sum[q[hh]]);
            while (hh < tt && (y(q[tt], k) - y(q[tt - 1], k)) * (i - q[tt]) >= (y(i, k) - y(q[tt], k)) * (q[tt] - q[tt - 1])) tt--;
            q[++tt] = i;
        }
    }
    printf("%lld\n", f[P][m]);
}

参考

• 【笔记】斜率优化DP复习笔记（普及+至省选）