第六届蓝桥杯（2015）C/C++大学A组省赛题解
第一题、方程整数解
答案：10 18 24，最小的为 10
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
for (int i = 1; i <= 40; ++i)
for (int j = 1; j <= 40; ++j)
for (int k = 1; k <= 40; ++k)
if (i * i + j * j + k * k == 1000) {
cout << i << " " << j << " " << k << "\n";
}
return 0;
}
第二题、星系炸弹
使用计算器
答案：2017-08-05
第三题、奇妙的数字
小明发现了一个奇妙的数字。它的平方和立方正好把0~9的10个数字每个用且只用了一次。
你能猜出这个数字是多少吗？
请填写该数字，不要填写任何多余的内容。
答案：69
写个程序跑一下即可
bool vis[10] = {false};
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
int n = 10;
while (true) {
for (int i = 0; i < 10; ++i) vis[i] = false;
int nn = n * n;
int nnn = nn * n;
while (nn) {
vis[nn % 10] = true;
nn /= 10;
}
while (nnn) {
vis[nnn % 10] = true;
nnn /= 10;
}
bool f = true;
for (int i = 0; i < 10 && f; ++i)
if (!vis[i]) f = false;
if (f) {
cout << n << "\n";
break;
}
n++;
}
return 0;
}
第四题、格子中输出
StringInGrid函数会在一个指定大小的格子中打印指定的字符串。
要求字符串在水平、垂直两个方向上都居中。
如果字符串太长，就截断。
如果不能恰好居中，可以稍稍偏左或者偏上一点。
下面的程序实现这个逻辑，请填写划线部分缺少的代码。
#include <stdio.h>
#include <string.h>
void StringInGrid(int width, int height, const char* s) {
int i, k;
char buf[1000];
strcpy(buf, s);
if (strlen(s) > width - 2) buf[width - 2] = 0;
printf("+");
for (i = 0; i < width - 2; i++) printf("-");
printf("+\n");
for (k = 1; k < (height - 1) / 2; k++) {
printf("|");
for (i = 0; i < width - 2; i++) printf(" ");
printf("|\n");
}
printf("|");
printf("%*s%s%*s", ______________________________); //填空
// 空格 + buf + 空格:
// (width - strlen(buf) - 2) / 2, buf, (width - strlen(buf) - 2 + 1) / 2
printf("|\n");
for (k = (height - 1) / 2 + 1; k < height - 1; k++) {
printf("|");
for (i = 0; i < width - 2; i++) printf(" ");
printf("|\n");
}
printf("+");
for (i = 0; i < width - 2; i++) printf("-");
printf("+\n");
}
int main() {
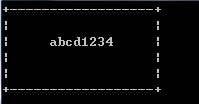
StringInGrid(20, 6, "abcd1234");
return 0;
}
第五题、九数组分数
1,2,3…9 这九个数字组成一个分数，其值恰好为1/3，如何组法？
下面的程序实现了该功能，请填写划线部分缺失的代码。
注意：只填写缺少的内容，不要书写任何题面已有代码或说明性文字。
#include <stdio.h>
void test(int x[]) {
int a = x[0] * 1000 + x[1] * 100 + x[2] * 10 + x[3];
int b = x[4] * 10000 + x[5] * 1000 + x[6] * 100 + x[7] * 10 + x[8];
if (a * 3 == b) printf("%d / %d\n", a, b);
}
void f(int x[], int k) {
int i, t;
if (k >= 9) {
test(x);
return;
}
for (i = k; i < 9; i++) {
{
t = x[k];
x[k] = x[i];
x[i] = t;
}
f(x, k + 1);
// 把数字交换回去
// t = x[k], x[k] = x[i], x[i] = t;
// _____________________________________________ // 填空处
}
}
int main() {
int x[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
f(x, 0);
return 0;
}
第六题、牌型种数
小明被劫持到X赌城，被迫与其他3人玩牌。
一副扑克牌（去掉大小王牌，共52张），均匀发给4个人，每个人13张。
这时，小明脑子里突然冒出一个问题：
如果不考虑花色，只考虑点数，也不考虑自己得到的牌的先后顺序，自己手里能拿到的初始牌型组合一共有多少种呢？
请填写该整数，不要填写任何多余的内容或说明文字。
解析：
如果小规模数据，全排列next-permutation是很好的方法，但是52！的排列是不可能是实现的，用dfs，每一种点数都有5种可能，不取，取一张，取两张，取三张，取四张，总和达到13直接退出，13步直接退出
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int ans = 0;
void dfs(int depth, int sum) {
if (depth == 13) {
if (sum == 13) ans++;
return;
}
if (sum > 13) return;
for (int i = 0; i < 5; ++i) dfs(depth + 1, sum + i);
}
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
dfs(0, 0);
cout << ans << "\n";
return 0;
}
第七题、手链样式
小明有3颗红珊瑚，4颗白珊瑚，5颗黄玛瑙。
他想用它们串成一圈作为手链，送给女朋友。
现在小明想知道：如果考虑手链可以随意转动或翻转，一共可以有多少不同的组合样式呢？
请你提交该整数。不要填写任何多余的内容或说明性的文字。
答案：1170
说实话，这道题没想太多，傻傻的填了2310，但是不对。
-
对于转动实际上就是每个数字都有可能成为队首，在next-permutation的排列下直接除以12即可，答案为2310，
-
对于翻转问题需要考虑翻转不会影响排列的情况，
将红、黄各取出1颗组成一条对称轴，剩下2个红，4个白，4个黄两边对称，也就是说，对称轴每一边都是1个红，2个白，2个黄，考虑这五个的排列，5！要除以2个白和2个黄的重复情况，5!除以2除以2，结果为30，（2310-30）/2就是会翻转会重复出现的情况，在加上翻转不会重复的情况
（2310-30）/2+30=1170
int a[12] = {1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3};
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
int ans = 0;
do ans++;
while (next_permutation(a, a + 12));
cout << ans / 12 << "\n"; // 输出: 2310
return 0;
}
第八题、饮料换购
乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊C型饮料，凭3个瓶盖可以再换一瓶C型饮料，并且可以一直循环下去(但不允许暂借或赊账)。
请你计算一下，如果小明不浪费瓶盖，尽量地参加活动，那么，对于他初始买入的n瓶饮料，最后他一共能喝到多少瓶饮料。
输入：一个整数n，表示开始购买的饮料数量（\(0<n<10000\)）
输出：一个整数，表示实际得到的饮料数
例如：
用户输入：
100
程序应该输出：
149
用户输入：
101
程序应该输出：
151
模拟题，用递归就能解决，需要注意的就是递归出口，当传入的参数小于3时退出循环！
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int cnt = 0;
void f(int x) {
if (x < 3) return;
int mod = x % 3, tmp = x / 3;
cnt += tmp;
f(mod + tmp);
}
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
int n;
cin >> n, f(n);
cout << cnt + n << "\n";
return 0;
}
第九题、垒骰子
赌圣atm晚年迷恋上了垒骰子，就是把骰子一个垒在另一个上边，不能歪歪扭扭，要垒成方柱体。
经过长期观察，atm 发现了稳定骰子的奥秘：有些数字的面贴着会互相排斥！
我们先来规范一下骰子：1 的对面是 4，2 的对面是 5，3 的对面是 6。
假设有 m 组互斥现象，每组中的那两个数字的面紧贴在一起，骰子就不能稳定的垒起来。
atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多，请输出模 10^9 + 7 的结果。
不要小看了 atm 的骰子数量哦～
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行，每行两个整数 a b ，表示 a 和 b 数字不能紧贴在一起。
「输出格式」
一行一个数，表示答案模 10^9 + 7 的结果。
「样例输入」
2 1
1 2
「样例输出」
544
「数据范围」
对于 30% 的数据：\(n \le 5\)
对于 60% 的数据：\(n \le 100\)
对于 100% 的数据：\(0 < n \le 10^9, m \le 36\)
// 待补
第十题、灾后重建
Pear市一共有N（<=50000）个居民点，居民点之间有M（<=200000）条双向道路相连。这些居民点两两之间都可以通过双向道路到达。这种情况一直持续到最近，一次严重的地震毁坏了全部M条道路。
震后，Pear打算修复其中一些道路，修理第i条道路需要Pi的时间。不过，Pear并不打算让全部的点连通，而是选择一些标号特殊的点让他们连通。
Pear有Q（<=50000）次询问，每次询问，他会选择所有编号在[l,r]之间，并且 编号 mod K = C 的点，修理一些路使得它们连通。由于所有道路的修理可以同时开工，所以完成修理的时间取决于花费时间最长的一条路，即涉及到的道路中Pi的最大值。
你能帮助Pear计算出每次询问时需要花费的最少时间么？这里询问是独立的，也就是上一个询问里的修理计划并没有付诸行动。
【输入格式】
第一行三个正整数N、M、Q，含义如题面所述。
接下来M行，每行三个正整数Xi、Yi、Pi，表示一条连接Xi和Yi的双向道路，修复需要Pi的时间。可能有自环，可能有重边。\(1<=Pi<=1000000\)。
接下来Q行，每行四个正整数Li、Ri、Ki、Ci，表示这次询问的点是[Li,Ri]区间中所有编号Mod Ki=Ci的点。保证参与询问的点至少有两个。
输出格式】
输出Q行，每行一个正整数表示对应询问的答案。
【样例输入】
7 10 4
1 3 10
2 6 9
4 1 5
3 7 4
3 6 9
1 5 8
2 7 4
3 2 10
1 7 6
7 6 9
1 7 1 0
1 7 3 1
2 5 1 0
3 7 2 1
【样例输出】
9
6
8
8
【数据范围】
对于20%的数据，N,M,Q<=30
对于40%的数据，N,M,Q<=2000
对于100%的数据，N<=50000,M<=2*10^5,Q<=50000. Pi<=10^6. Li,Ri,Ki均在[1,N]范围内，Ci在[0,对应询问的Ki)范围内。
// 待补
