2014年第五届蓝桥杯【C++省赛B组】
第一题：啤酒和饮料
啤酒每罐2.3元，饮料每罐1.9元。小明买了若干啤酒和饮料，一共花了82.3元。
我们还知道他买的啤酒比饮料的数量少，请你计算他买了几罐啤酒。
注意：答案是一个整数。请通过浏览器提交答案。
不要书写任何多余的内容（例如：写了饮料的数量，添加说明文字等）。
暴力即可
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
for (int i = 1; i <= (int)(82.3 / 1.9); ++i)
for (int j = 0; j < i; ++j)
if (i * 1.9 + j * 2.3 == 82.3) {
cout << j << "\n";
return 0;
}
return 0;
}
// 答案：11
第二题：切面条
一根高筋拉面，中间切一刀，可以得到2根面条。
如果先对折1次，中间切一刀，可以得到3根面条。
如果连续对折2次，中间切一刀，可以得到5根面条。
那么，连续对折10次，中间切一刀，会得到多少面条呢？
答案是个整数，请通过浏览器提交答案。不要填写任何多余的内容。
在手写一个例子后，发现规律为：\(a[i] = 2 * a[i-1] - 1\)
所以直接按公式写即可
答案：1025
第三题：李白打酒
话说大诗人李白，一生好饮。幸好他从不开车。
一天，他提着酒壶，从家里出来，酒壶中有酒2斗。他边走边唱：
无事街上走，提壶去打酒。
逢店加一倍，遇花喝一斗。
这一路上，他一共遇到店5次，遇到花10次，已知最后一次遇到的是花，他正好把酒喝光了。
请你计算李白遇到店和花的次序，可以把遇店记为a，遇花记为b。则：babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢？请你计算出所有可能方案的个数（包含题目给出的）。
注意：通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。
思路一：递归，dfs搜索全部方案（全排列），在出口处筛选条件（5个店、10次花、酒数位0、最后一次遇到的是花...）
int cnt = 0;
void dfs(string s, int pos, int shop, int flower, int num) {
if (num < 0) return;
if (pos == 16 && num == 0) {
if (s[15] == 'b' && num == 0) cnt++;
return;
}
if (shop > 0) {
s[pos] = 'a';
dfs(s, pos + 1, shop - 1, flower, num * 2);
s[pos] = '0';
}
if (flower > 0) {
s[pos] = 'b';
dfs(s, pos + 1, shop, flower - 1, num - 1);
s[pos] = '0';
}
}
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
string s = "000000000000000000000";
int shop = 5, flower = 10;
dfs(s, 1, shop, flower, 2);
cout << cnt;
return 0;
}
// 14
思路二：递归，dfs搜索前14个位置，放入5个店的方案，筛选条件（正好把酒喝完）
思路三：二进制枚举
int main() {
ios_base::sync_with_stdio(false), cin.tie(0);
int sum = 0, shop = 0, flower = 0, cnt = 0;
for (int i = 0; i < (1 << 14); ++i) { // 2^14-1种方案
sum = 2, shop = flower = 0;
//枚举当前方案每一位,当前位是1表示是花 0表示是酒店
for (int j = 0; j < 14; ++j) {
if (i & (1 << j)) flower++, sum--;
else
shop++, sum *= 2;
}
// 最后一个位置为花
if (flower == 9 && shop == 5 && sum == 1) cnt++;
}
cout << cnt << "\n";
return 0;
}
第四题：史丰收速算
史丰收速算法的革命性贡献是：从高位算起，预测进位。不需要九九表，彻底颠覆了传统手算!
速算的核心基础是：1位数乘以多位数的乘法。
其中，乘以7是最复杂的，就以它为例。
因为，1/7 是个循环小数：0.142857...，如果多位数超过 142857...，就要进1
同理，2/7, 3/7, ... 6/7 也都是类似的循环小数，多位数超过 n/7，就要进n
下面的程序模拟了史丰收速算法中乘以7的运算过程。
乘以 7 的个位规律是：偶数乘以2，奇数乘以2再加5，都只取个位。
乘以 7 的进位规律是：
满 142857... 进1,
满 285714... 进2,
满 428571... 进3,
满 571428... 进4,
满 714285... 进5,
满 857142... 进6
请分析程序流程，填写划线部分缺少的代码。
//计算个位
int ge_wei(int a)
{
if(a % 2 == 0)
return (a * 2) % 10;
else
return (a * 2 + 5) % 10;
}
//计算进位
int jin_wei(char* p)
{
char* level[] = {
"142857",
"285714",
"428571",
"571428",
"714285",
"857142"
};
char buf[7];
buf[6] = '\0';
strncpy(buf,p,6);
int i;
for(i=5; i>=0; i--){
int r = strcmp(level[i], buf);
if(r<0) return i+1;
while(r==0){
p += 6;
strncpy(buf,p,6);
r = strcmp(level[i], buf);
if(r<0) return i+1;
______________________________; //填空
}
}
return 0;
}
//多位数乘以7
void f(char* s)
{
int head = jin_wei(s);
if(head > 0) printf("%d", head);
char* p = s;
while(*p){
int a = (*p-'0');
int x = (ge_wei(a) + jin_wei(p+1)) % 10;
printf("%d",x);
p++;
}
printf("\n");
}
int main()
{
f("428571428571");
f("34553834937543");
return 0;
}
答案：if(r>0) return i;
思路：分析题目，理清楚何时进位
第五题：打印图形
小明在X星球的城堡中发现了如下图形和文字：
rank=3
rank=5
ran=6
小明开动脑筋，编写了如下的程序，实现该图形的打印。
#define N 70 void f(char a[][N], int rank, int row, int col) { if(rank==1){ a[row][col] = '*'; return; } int w = 1; int i; for(i=0; i<rank-1; i++) w *= 2; ____________________________________________; f(a, rank-1, row+w/2, col); f(a, rank-1, row+w/2, col+w); } int main() { char a[N][N]; int i,j; for(i=0;i<N;i++) for(j=0;j<N;j++) a[i][j] = ' '; f(a,6,0,0); for(i=0; i<N; i++){ for(j=0; j<N; j++) printf("%c",a[i][j]); printf("\n"); } return 0; }
第六题：奇怪的分式
上小学的时候，小明经常自己发明新算法。一次，老师出的题目是：
1/4 乘以 8/5
小明居然把分子拼接在一起，分母拼接在一起，答案是：18/45 （参见图1.png）
老师刚想批评他，转念一想，这个答案凑巧也对啊，真是见鬼！
对于分子、分母都是 1~9 中的一位数的情况，还有哪些算式可以这样计算呢？
请写出所有不同算式的个数（包括题中举例的）。
显然，交换分子分母后，例如：4/1 乘以 5/8 是满足要求的，这算做不同的算式。
但对于分子分母相同的情况，2/2 乘以 3/3 这样的类型太多了，不在计数之列!
注意：答案是个整数（考虑对称性，肯定是偶数）。请通过浏览器提交。不要书写多余的内容。
思路一：dfs全排列，最后筛选条件
代码一：
int a[6];
int ans = 0;
//求最大公约数
int gcd(int xx, int yy) { return yy == 0 ? xx : gcd(yy, xx % yy); }
//测试条件是否满足
bool test() {
if (a[1] == a[2] && a[3] == a[4]) return false;
if (a[1] == a[3] && a[2] == a[4]) return false;
int x = gcd(a[2] * a[4], a[1] * a[3]);
int y = gcd(10 * a[2] + a[4], 10 * a[1] + a[3]);
//同分、化简后再比较两个分数
if ((a[2] * a[4]) / x == (10 * a[2] + a[4]) / y &&
(a[1] * a[3]) / x == (10 * a[1] + a[3]) / y) {
return true;
}
return false;
}
/*
参数x表示第几个位置
b/a c/d，这里 a是a[1]即第一个位置，b是a[2] 即第二个位置 d是a[3] c是a[4]
*/
void dfs(int x) {
if (x == 5) {
if (test()) {
ans++;
// for (int i = 1; i <= 4; i++) {
// cout << a[i] << " ";
// }
// cout << endl;
return;
}
return;
}
//每个位置都可以填9个数
for (int i = 1; i <= 9; i++) {
a[x] = i;
dfs(x + 1); //搜索下一个位置
}
}
int main() {
dfs(1); //从a这个位置开始搜索，也就是第一个位置
cout << ans << endl;
}
来自 fisherss 学长的建议
思路二：也可以暴力枚举，四成循环。蓝桥杯这种暴力解题很常见！
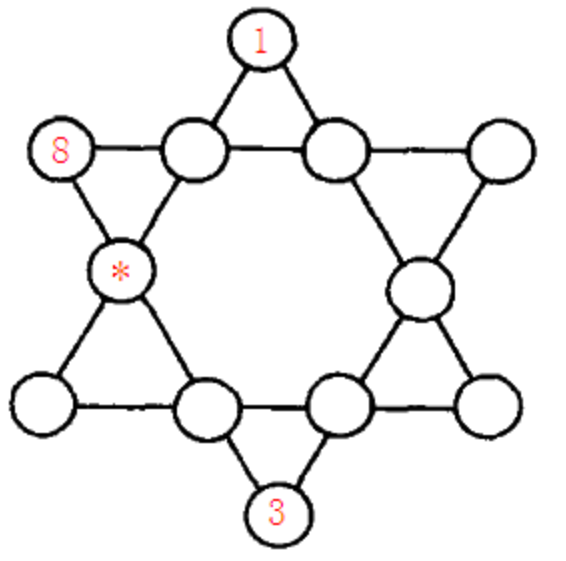
第七题：六角填数
如图所示六角形中，填入1~12的数字。
使得每条直线上的数字之和都相同。
图中，已经替你填好了3个数字，请你计算星号位置所代表的数字是多少？
请通过浏览器提交答案，不要填写多余的内容。
思路：dfs搜索所有方案，参数k表示当前是第k个位置上的搜索
//求解a[6]的值
int a[15]; //从上到下从左到右，存放各个位置填的值
int visited[13]; //判断是否用过1~12这几个数
int b[6]; //共6个直线
/*检查是否满足条件*/
bool test() {
b[0] = a[2] + a[3] + a[4] + a[5];
b[1] = a[1] + a[3] + a[6] + a[8];
b[2] = a[2] + a[6] + a[9] + a[12];
b[3] = a[5] + a[7] + a[10] + a[12];
b[4] = a[1] + a[4] + a[7] + a[11];
b[5] = a[8] + a[9] + a[10] + a[11];
//判断是否有不相等的 直接return 不满足
for (int i = 0; i <= 5; i++)
for (int j = 0; j <= 5; j++)
if (b[i] != b[j]) return false;
return true;
}
// dfs搜索，参数k表示第几个位置
void dfs(int k) {
if (k == 12) {
//...检查是否满足要求
if (test()) cout << a[6] << endl;
return;
}
for (int i = 1; i <= 12; i++) {
if (!visited[i]) {
visited[i] = 1;
a[k] = i;
dfs(k + 1);
visited[i] = 0;
}
}
}
int main() {
//初始化
a[1] = 1, a[2] = 8, a[12] = 3;
visited[1] = 1, visited[8] = 1, visited[3] = 1;
dfs(3); //从第3个位置开始dfs
}
第八题：蚂蚁感冒
长100厘米的细长直杆子上有n只蚂蚁。它们的头有的朝左，有的朝右。
每只蚂蚁都只能沿着杆子向前爬，速度是1厘米/秒。
当两只蚂蚁碰面时，它们会同时掉头往相反的方向爬行。
这些蚂蚁中，有1只蚂蚁感冒了。并且在和其它蚂蚁碰面时，会把感冒传染给碰到的蚂蚁。
请你计算，当所有蚂蚁都爬离杆子时，有多少只蚂蚁患上了感冒。
【数据格式】
第一行输入一个整数n (1 < n < 50), 表示蚂蚁的总数。
接着的一行是n个用空格分开的整数 Xi (-100 < Xi < 100), Xi的绝对值，表示蚂蚁离开杆子左边端点的距离。正值表示头朝右，负值表示头朝左，数据中不会出现0值，也不会出现两只蚂蚁占用同一位置。其中，第一个数据代表的蚂蚁感冒了。
要求输出1个整数，表示最后感冒蚂蚁的数目。
例如，输入：
3
5 -2 8
程序应输出：
1
再例如，输入：
5
-10 8 -20 12 25
程序应输出：
3
第九题：地宫取宝
X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。
地宫的入口在左上角，出口在右下角。
小明被带到地宫的入口，国王要求他只能向右或向下行走。
走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。
当小明走到出口时，如果他手中的宝贝恰好是k件，则这些宝贝就可以送给小明。
请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这k件宝贝。
【数据格式】
输入一行3个整数，用空格分开：n m k (1<=n,m<=50, 1<=k<=12)
接下来有 n 行数据，每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值
要求输出一个整数，表示正好取k个宝贝的行动方案数。该数字可能很大，输出它对 1000000007 取模的结果。
例如，输入：
2 2 2
1 2
2 1
程序应该输出：
2
再例如，输入：
2 3 2
1 2 3
2 1 5
程序应该输出：
14
思路："记忆化搜索" 模拟走格子，再出口处判断是否满足条件，注意出口处有细节点（代码中解释）
这里偷懒了，拿 fisherss 学长的代码做示意
long long ans = 0;
int arr[100][100];
int n, m, k;
int have[10010];
//判断是否能拿走当前坐标上的物件
bool canTake(int x, int y, int t) {
for (int i = 1; i <= t; i++)
if (have[i] >= arr[x][y]) return false;
return true;
}
// dfs走格子
void dfs(int x, int y, int t) {
if (x == n && y == m) {
// （1）可能不算右下角的也正好
// （2）如果右下角的比当前的大，算上这一个如果正好也可以增加路径
if (t == k + 1 || (t == k && canTake(n, m, t))) {
ans++;
ans = ans % 1000000007;
}
return;
}
if (canTake(x, y, t)) {
have[t] = arr[x][y];
if (x + 1 <= n) dfs(x + 1, y, t + 1);
if (y + 1 <= m) dfs(x, y + 1, t + 1);
have[t] = -1;
}
if (x + 1 <= n) dfs(x + 1, y, t); //走右边
if (y + 1 <= m) dfs(x, y + 1, t); //走下边
}
int main() {
cin >> n >> m >> k;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) cin >> arr[i][j];
for (int i = 1; i <= k; i++) have[i] = -1;
dfs(1, 1, 1); //横坐标 纵坐标 件数
cout << ans << endl;
}
记忆型递归：就是“缓存”，使用数组或者map等等。存储当前状态对应的值（这里就是当前dfs参数下对应的方案数），
为什么要使用记忆型递归？因为中间结果重复过多，为了提高效率。
第十题：小朋友排队
n 个小朋友站成一排。现在要把他们按身高从低到高的顺序排列，但是每次只能交换位置相邻的两个小朋友。
每个小朋友都有一个不高兴的程度。开始的时候，所有小朋友的不高兴程度都是0。
如果某个小朋友第一次被要求交换，则他的不高兴程度增加1，如果第二次要求他交换，则他的不高兴程度增加2（即不高兴程度为3），依次类推。当要求某个小朋友第k次交换时，他的不高兴程度增加k。
请问，要让所有小朋友按从低到高排队，他们的不高兴程度之和最小是多少。
如果有两个小朋友身高一样，则他们谁站在谁前面是没有关系的。
【数据格式】
输入的第一行包含一个整数n，表示小朋友的个数。
第二行包含 n 个整数 H1 H2 … Hn，分别表示每个小朋友的身高。
输出一行，包含一个整数，表示小朋友的不高兴程度和的最小值。
例如，输入：
3
3 2 1
程序应该输出：
9
【样例说明】
首先交换身高为3和2的小朋友，再交换身高为3和1的小朋友，再交换身高为2和1的小朋友，每个小朋友的不高兴程度都是3，总和为9。
【数据规模与约定】
对于10%的数据， 1<=n<=10；
对于30%的数据， 1<=n<=1000；
对于50%的数据， 1<=n<=10000；
对于100%的数据，1<=n<=100000，0<=Hi<=1000000。
使用树状数组优化，求逆序对(左边大于它的 + 右边小于它的数量),求完逆序对后,计算等差数列和 (因为不高兴程度每次增加k)
先熟悉树状数组原理及其应用。
1.这道题可以转换成求每个位置的左边比他小的个数和右边比他大的个数，这两个相加就是这个人要被交换的次数，然后根据等差数列前n项求和公式(a1+an)*n/2，将所有位置和相加即可。
2.求逆序数用树状数组优化成 nlogm,树状数组是专门用来求前缀和的，这里从位置0遍历到n-1，把高度作为树状数组的下标，每个高度对应的个数作为树状数组的值，对于输入的小朋友高度a[i]，在当前小朋友左边&&比当前小朋友a[i]高的总数，就是树状数组s(maxh)-s(a[i])=i+1-s(a[i])，反之同理。
注意事项:
1.题中a[i]可以等于0，所以要把输入加一，不然在后面计算sum(a[i]-1)处，会越界。
2.代码中a数组是保存输入,d数组的下标是高度，lr数组是保存位置i的左右逆序总数,maxh是输入的最大值
// fisherss Code
#include <cstdio>
#include <iostream>
#define _for(i, a, b) for (int i = a; i < b; i++)
#define _unfor(i, a, b) for (int i = a; i >= b; i--)
#define mset(a, val, n) \
for (int i = 0; i < n; i++) a[i] = val;
#define lowbit(x) (x & (-x))
using namespace std;
typedef long long LL;
int a[100005], d[1000005], n, lr[100005], maxh = 0;
// tree_arr
void add(int i, int x) {
while (i <= maxh + 1) d[i] += x, i += lowbit(i);
}
int sum(int i) {
int res = 0;
while (i > 0) res += d[i], i -= lowbit(i);
return res;
}
//
int main() {
scanf("%d", &n);
_for(i, 0, n) {
scanf("%d", &a[i]);
maxh = max(maxh, ++a[i]);
}
_for(i, 0, n) {
add(a[i], 1);
lr[i] += i + 1 - sum(a[i]);
}
mset(d, 0, maxh + 5);
_unfor(i, n - 1, 0) {
add(a[i], 1);
lr[i] += sum(a[i] - 1);
}
LL ans = 0;
_for(i, 0, n) {
LL k = lr[i];
ans += k * (k + 1) / 2;
}
cout << ans << endl;
}
