特殊的数据结构:主席树
最近学习了下主席树,发现比想象中简单,又发现网上的讲解比较复杂,于是自己写一篇简易的指南,较难的问题慢慢补吧。
什么是主席树呢
让我们来看一个经典的问题吧:
给定一个[1,n]的区间,m次操作,操作种类如下:
1 L R:查询[L,R]的区间和
2 L R X:将[L,R]的值加上X
这种经典问题,想必大家学过线段树后都可以轻松解决。然而如果再增加一种操作:
3 K:回退到第K次修改操作的结果
可见,如果题目要求回溯到历史版本,那么普通的线段树就不能解决了,因为在每次更新操作后,线段树存储的内容就发生了改变,如果不进行特殊记录,那么这种改变将是永久的。因此,对于这种类型的题目,我们可以用到今天要讨论的数据结构——主席树来进行解决。
主席树的实质,就是以最初的线段树作为模板,通过"结点复用“的方式,实现存储多个线段树。说的准确一点,他是 \(n\) 棵完整的权值线段树,但是这 \(n\) 棵树之间共用一些节点,使得内存开销仅为 \((nlogn)\),由于权值线段树之间可以加减,所以我们可以得到序列任意区间的一棵权值线段树。
主席树是怎么实现的
首先由于主席树是一颗可持久化线段树,所以他本质上是一棵线段树(这不是废话吗),所以我们先画一棵可爱的线段树。
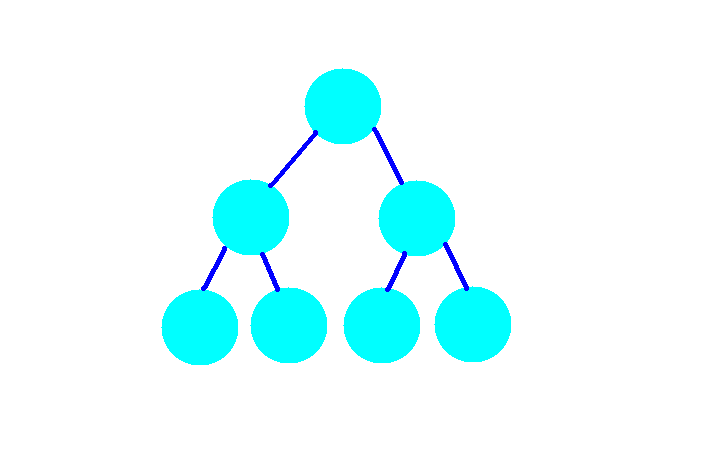
然后我们对其中一个无辜的叶子节点进行修改,正常来说如果我们要存储之前没修改的历史版本,我们就可以再对修改过点的新线段树再新建一个新线段树,这样我们就一共有两棵完整的线段树了,就像下面一样。
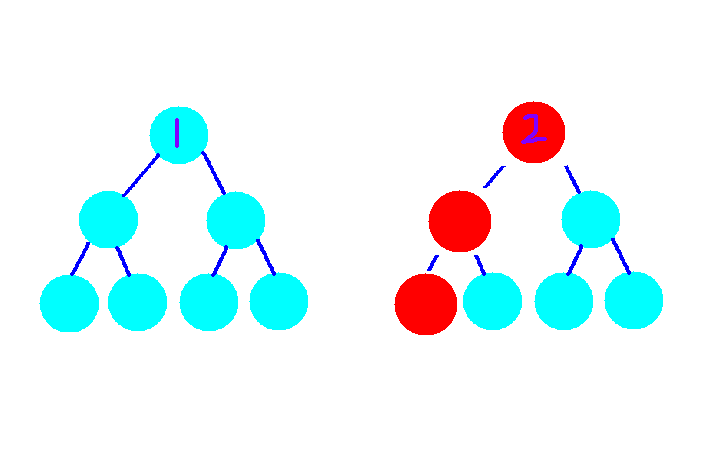
但通过肉眼的观察我们发现,只有红色部分,也就是从被修改的叶子节点到根节点的一条链被修改了。所以我们就想能不能两棵线段树共用没有修改的节点呢?
当然可以啊,这样我们就只要在新的线段树上新建一条链,然后没有修改的子节点就直接指向之前的那棵线段树,这样就可以在只增加一条链的空间复杂度和时间复杂度的代价下存储下了新的那棵历史版本的线段树。
一下讲那么多可以难以理解,现在再搭配一道经典题来理解吧:【POJ 2104 K-th Number】(静态区间求第K大)。
【Description】
You are working for Macrohard company in data structures department. After failing your previous task about key insertion you were asked to write a new data structure that would be able to return quickly k-th order statistics in the array segment.
That is, given an array a[1...n] of different integer numbers, your program must answer a series of questions Q(i, j, k) in the form: "What would be the k-th number in a[i...j] segment, if this segment was sorted?"
For example, consider the array a = (1, 5, 2, 6, 3, 7, 4). Let the question be Q(2, 5, 3). The segment a[2...5] is (5, 2, 6, 3). If we sort this segment, we get (2, 3, 5, 6), the third number is 5, and therefore the answer to the question is 5.【Input】
The first line of the input file contains n --- the size of the array, and m --- the number of questions to answer (1 <= n <= 100 000, 1 <= m <= 5 000).
The second line contains n different integer numbers not exceeding 109 by their absolute values --- the array for which the answers should be given.
The following m lines contain question descriptions, each description consists of three numbers: i, j, and k (1 <= i <= j <= n, 1 <= k <= j - i + 1) and represents the question Q(i, j, k).【Output】
For each question output the answer to it --- the k-th number in sorted a[i...j] segment.
题目大意:就是很简单的给出一个长为n的序列a,然后给出m个询问,每次给出三个数x,y,k,然后需要我们求出在序列a的区间【x,y】中,第k大的数是哪个。
一看到第k大数,我们蒟蒻的第一反应就是权值线段树(有更加高级算法的大佬轻喷)。如果题目求的是整个区间的第k大数,确实可以直接用裸的权值线段树【若排序后第一个数到第x个数一共有k个数,那么这个x就是第k大数】。
但是这道题需要我们求解的是区间【x,y】中的第k大数,这时我们就想,能不能对于任意【1,i】都开一棵权值线段树呢?没错,这就是正解——主席树。我们只要对于每个点i都开一棵只有一条链的不完整线段树,剩下的未修改的节点,就直接指向第i-1个节点那些子节点就可以了。
思路已经很清晰了,下面我们就一步一步来完成这个算法。
首先我们发现序列a中的数很大,直接开权值线段树肯定爆炸,所以我们需要离散化,下面给出vector离散化的模板:
//离散化代码
int getid(int x) {
return (lower_bound(v.begin(), v.end(), x) - v.begin() + 1);
} //求出原来的数字在离散化以后的数字
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]), v.push_back(a[i]); //读取序列a【i】
sort(v.begin(), v.end()), v.erase(unique(v.begin(), v.end()),
v.end()); //对序列进行离散
接下来我们就只要对每个点建一棵线段树,然后我们知道权值线段树是具有可加可减性的,所以在查询【x,y】区间的时候,只要将第y棵权值线段树(【1,y】)减去第x-1棵权值线段树(【1,x-1】),得到的就是【x,y】的权值线段树。
所以基本的核心代码就呼之欲出了:
for (int i = 1; i <= n; i++) update(1, n, root[i], root[i - 1], getid(a[i]));
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &x, &y, &k);
printf("%d\n", v[query(1, n, root[x - 1], root[y], k) - 1]);
}
return 0;
剩下的问题就是,怎么样完成构建的update操作和查询的query操作了;
首先是update操作:
void update(int l, int r, int &x, int y, int pos) {
T[++cnt] = T[y], T[cnt].sum++, x = cnt;
int mid = (l + r) / 2;
if (l == r) return;
if (pos <= mid)
update(l, mid, T[x].l, T[y].l, pos);
else
update(mid + 1, r, T[x].r, T[y].r, pos);
}
l,r是区间的范围,x,y是线段树节点在T数组里的位置,pos为要加入的权值。接下来就很显然了,我们先新建一个空间,刚开始时左右儿子都和前一棵线段树一样,然后我们就判断要增加的权值在左半部分还是右半部分,然后就逐层修改所需增加的权值就可以了。
然后是query操作:
int query(int l, int r, int x, int y, int k) {
if (l == r) return (l);
int sum = T[T[y].l].sum - T[T[x].l].sum; //求出【l,r】的权值线段树。
int mid = (l + r) / 2;
if (k <= sum) return (query(l, mid, T[x].l, T[y].l, k));
else return (query(mid + 1, r, T[x].r, T[y].r, k - sum));
}
相似的,我们只需要像修改步骤一样,逐层找到权值线段树中的第k个节点是谁,就可以求出第k大数了。
所以总的程序就很短小:
#include <bits/stdc++.h>
using namespace std;
const int Maxx = 1e5 + 6;
int n, m, cnt, a[Maxx], root[Maxx], x, y, k;
struct node {
int l, r, sum;
} T[Maxx * 40];
vector<int> v;
int getid(int x) {
return (lower_bound(v.begin(), v.end(), x) - v.begin() + 1);
}
void update(int l, int r, int &x, int y, int pos) {
T[++cnt] = T[y], T[cnt].sum++, x = cnt;
int mid = (l + r) / 2;
if (l == r) return;
if (pos <= mid)
update(l, mid, T[x].l, T[y].l, pos);
else
update(mid + 1, r, T[x].r, T[y].r, pos);
}
int query(int l, int r, int x, int y, int k) {
if (l == r) return (l);
int sum = T[T[y].l].sum - T[T[x].l].sum;
int mid = (l + r) / 2;
if (k <= sum)
return (query(l, mid, T[x].l, T[y].l, k));
else
return (query(mid + 1, r, T[x].r, T[y].r, k - sum));
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]), v.push_back(a[i]);
sort(v.begin(), v.end()), v.erase(unique(v.begin(), v.end()), v.end());
for (int i = 1; i <= n; i++)
update(1, n, root[i], root[i - 1], getid(a[i]));
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &x, &y, &k);
printf("%d\n", v[query(1, n, root[x - 1], root[y], k) - 1]);
}
return 0;
}
尾声
希望读了这篇文章的您能有收获,如果有不懂的,可以私信我,我会完善我的文章,争取让每个人都能读懂!



