哈夫曼树的构建、编码以及带权路径长计算
本文转载自：https://blog.csdn.net/yushupan/article/details/82735773?utm_source=app
给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。
构造哈夫曼树的算法如下：
1）对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F={T1,T2,T3,...,Ti,..., Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。
2）在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。
3）从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。
4）重复2）和3），直到集合F中只有一棵二叉树为止。
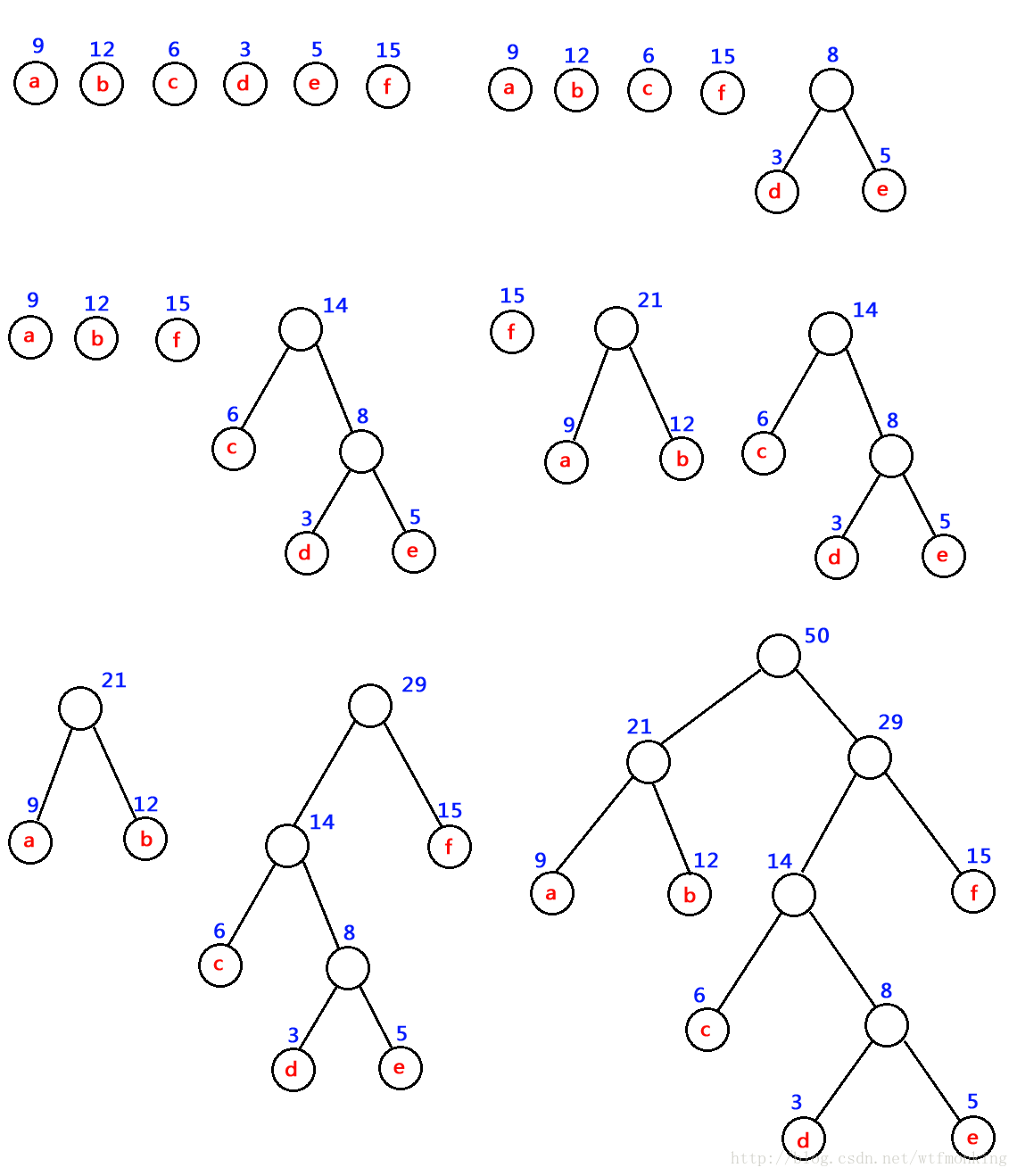
假设给定a、b、c、d、e、f的权值分别为{9, 12, 6, 3, 5, 15}，构造哈夫曼树的过程如下：
1、为了方便起见，首先将权值进行从小到大排序即,3, 5, 6, 9,12,15
2、选取最小的两个权值3和5构建子树。3+5 = 8作为3,5的父节点（我们规定要满足左子节点小于右子节点）
3、顺序提取6作为左子节点，8作为右子节点。将6+8 = 14作为其父节点。
4、我们发现14大于接下来的9,12。故将9,12作为子节点，9+12 = 21为其父节点构建一个子树。提取元素15，作为右节点上一步构建的14作为左节点，将14+15 = 29作为他们的父节点构建另一个子树。
5、最后将上述两个子树的父节点21,29分别作为左节点和右节点。将21+29 = 50作为他们的父节点。这样就构造出了一个哈夫曼树。
接下来进行带权路径长的计算：
a，b，f（权值9,12,15）三个元素距父节点的距离都为2
c（权值6）元素距父节点的距离为3
d，e（权值3,5）元素距父节点的距离为4
故这棵哈夫曼树的WPL为：WPL =（9 + 12 + 15）2 + 6 * 3 + （3 + 5） 4 = 122
两种方法求解WPL：
（1）各叶子结点权值和路径长度之积的和。
（2）所有非叶子结点的权值之和。
哈夫曼编码
根据哈夫曼树可以解决报文编码问题。假设需要一个字符串“aaaabbbbccccdddeeeeffffaaaabbbbcceffffabbbbfffffff”进行编码，将它转换为唯一的二进制码，但要求转换出来的二进制编码的长度最小。
该字符串中正好满足a、b、c、d、e、f分别出现9, 12, 6, 3, 5, 15次，作为他们的权值。按照上述方法构建好哈夫曼树。
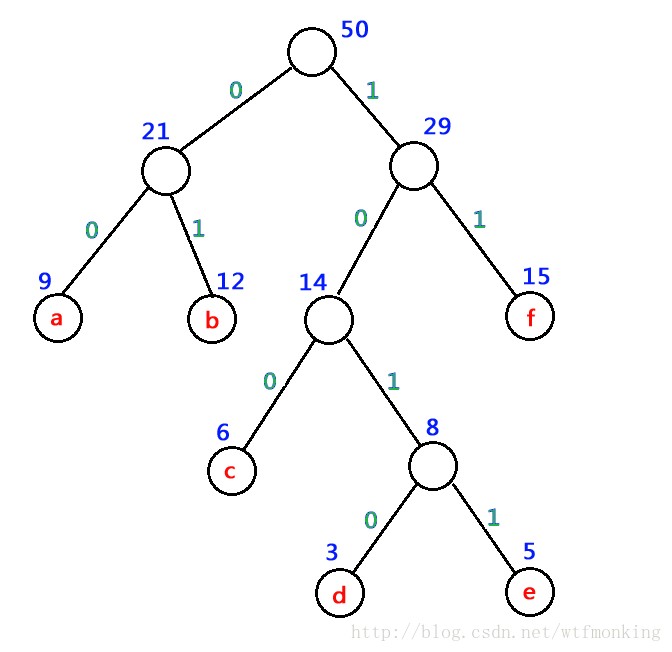
从哈夫曼树根节点开始，对左子树分配代码“0”，对右子树分配“1”，一直到达叶子节点。然后，将从树根沿着每条路径到达叶子节点的代码排列起来，便得到每个叶子节点的哈夫曼编码，如下右图。
从图中可以看出：
a 的编码为：00
b 的编码为：01
c 的编码为：100
d 的编码为：1010
e 的编码为：1011
f 的编码为：11
参考：
https://www.cnblogs.com/luankun0214/p/4423648.html?utm_source=tuicool&utm_medium=referral
