摩尔投票算法( Boyer-Moore Voting Algorithm)

update：21/07/24

前言

绝对众数。在数列 \(p\) 中出现次数严格大于 \(\frac{\vert p \vert}{2}\) 的数叫做绝对众数。

快速排序

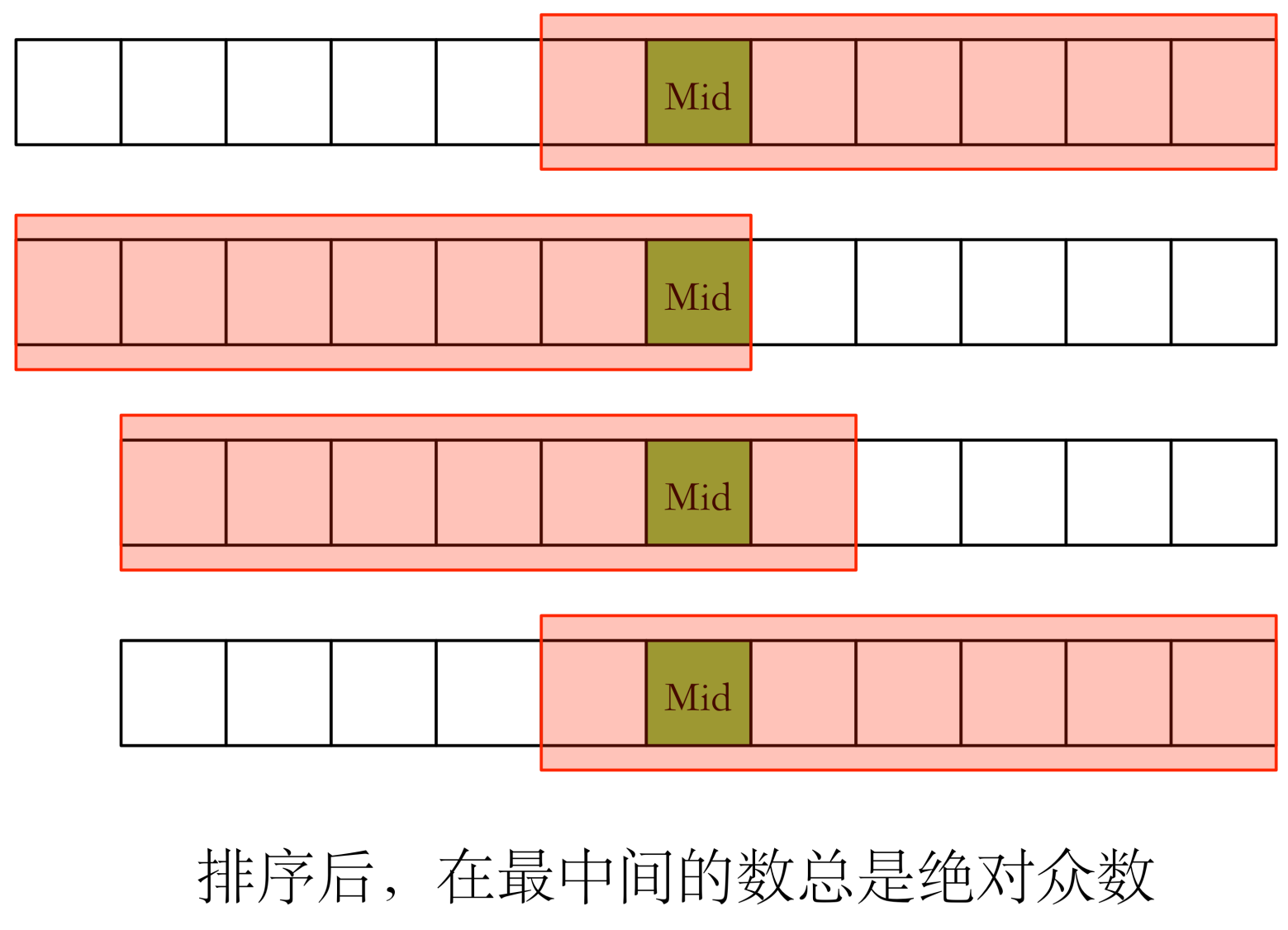
一般来说我们可以直接排序解决问题，如果存在绝对众数的话，最中间的数一定是绝对众数。

时间复杂度为 \(\mathcal{O}(n\ log n)\)

摩尔投票算法

摩尔投票法的基本思想很容易理解，在每一轮投票过程中，从数组中找出一对不同的元素，将其从数组中删除。循环执行这一操作，直到无法再进行投票，如果数组为空，则没有任何元素出现的次数超过该数组长度的一半（无绝对众数）。如果只存在一种元素，那么这个元素则可能为绝对众数。
在编写算法的过程中，我们可以直接按照数组原来的顺序进行投票，删除。
具体实现：设 \(num\) 为当前出现阶段超过半数的元素（候选数），\(cnt\) 为此元素出现次数。由于有了阶段的概念，这其实这也是一种动态规划思想。

一开始 \(num\) 直接为数组第一个元素，\(cnt = 1\)。（原因是只有一个元素的数组，唯一的那个元素一定是绝对众数）
接着遍历数列 \(p\)，设当前数为 \(k\) .

• 若 \(k = num\)，则 \(cnt + 1\)。
• 若 \(k \not = num\)，则我们可以把当前候选数和当前数同时删除，具体操作就是让 \(cnt - 1\)，这样就相当于忽略了数 \(k\)，删去一个 \(num\)。
• 若 \(cnt = 0\)，表明前一阶段并没有出现次数超过半数的元素。假设绝对众数存在，那么绝对众数一定在剩余的数组中是绝对众数，这样我们只需要求解原始问题的子问题即可，即在后一阶段的绝对众数是多少。回到开始， \(num\) 为当前元素，\(cnt = 1\)。

最终，若 \(cnt > 0\)，则 \(num\) 可能为候选元素。扫一遍数组确认一下即可。
复杂度为线性的，\(O(n)\)。

void majorityElement(vector<int>& p) {  
    int num = -1, cnt = 0;
    for(int i = 0; i < p.size(); ++i) {
        if(cnt == 0) num = p[i], cnt++;
        else if(p[i] == num) cnt++;
        else cnt--;        
    }
    cnt = 0;
    for(int i = 0; i < p.size(); ++i)
        if(p[i] == num) cnt++;
    if(cnt > p.size() / 2) printf("Found: %d\n", num);
    else printf("Not Found\n");
}

摩尔投票算法的改进：

1，题目： LeetCode 229 [Majority Element II]
给定一个整型数组，找到所有主元素，它在数组中的出现次数严格大于数组元素个数的三分之一。

算法：每次删除三个不相同的数，最后留下的一定是出现次数超过1/3的数，这个思想可以推广到出现次数超过1/k次的元素有哪些。

因为出现次数大于n/3的元素最多只有两个，所以最开始可以维护两个数字(num1,num2)和两个计数器 \((counter1,counter2)\)；
遍历数组，当数组中元素和num1或者num2相同，对应的counter1或者counter2加1；
如果counter1或counter2为0，将遍历到的该元素赋给num1或者nums2；
否则counter1和counter2都减1。

C++代码

class Solution {
public:
    vector<int> majorityElement(vector<int>& nums) {
        vector<int> re;
        if (nums.size()==0) return re;
        int candidate1 = 0;
        int count1 = 0;
        int candidate2 = 0;
        int count2 = 0;
        for (int i=0; i<nums.size(); i++) {
            if (nums[i] == nums[candidate1]) count1++;
            else if (nums[i] == nums[candidate2]) count2++;
            else if (count1==0) {
                candidate1 = i;
                count1 = 1;
            }
            else if (count2==0) {
                candidate2 = i;
                count2 = 1;
            }
            else {
                count1--;
                count2--;
            }
        }
        count1 = 0;
        count2 = 0;
        for (int i=0; i<nums.size(); i++) {
            if (nums[i] == nums[candidate1]) count1++;
            else if (nums[i] == nums[candidate2]) count2++;
        }
        if (count1 > nums.size()/3) re.push_back(nums[candidate1]);
        if (count2 > nums.size()/3) re.push_back(nums[candidate2]);
        return re;
    }
};