全网最!详!细!tarjan算法讲解

时隔好久回来复习tarjan算法，又看了许多网上的文章，在此再给一篇觉得不错的文章：mengxiang000

全网最详细tarjan算法讲解，我不敢说别的。反正其他tarjan算法讲解，我看了半天才看懂。我写的这个，读完一遍，发现原来tarjan这么简单！

tarjan算法，一个关于 图的联通性的神奇算法。基于DFS（迪法师）算法，深度优先搜索一张有向图。！注意！是有向图。根据树，堆栈，打标记等种种神（che）奇（dan）方法来完成剖析一个图的工作。而图的联通性，就是任督二脉通不通。。的问题。
了解tarjan算法之前你需要知道：
强连通，强连通图，强连通分量，解答树（解答树只是一种形式。了解即可）
不知道怎么办！！！

神奇海螺～：嘟噜噜～！
强连通(strongly connected)： 在一个有向图G里，设两个点 a b 发现，由a有一条路可以走到b，由b又有一条路可以走到a，我们就叫这两个顶点（a，b）强连通。

强连通图： 如果 在一个有向图G中，每两个点都强连通，我们就叫这个图，强连通图。

强连通分量strongly connected components)：在一个有向图G中，有一个子图，这个子图每2个点都满足强连通，我们就叫这个子图叫做 强连通分量 ［分量：：把一个向量分解成几个方向的向量的和，那些方向上的向量就叫做该向量（未分解前的向量）的分量］
举个简单的栗子：

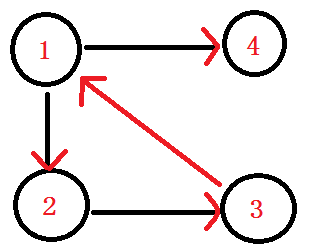
比如说这个图，在这个图中呢，点1与点2互相都有路径到达对方，所以它们强连通.

而在这个有向图中，点1 2 3组成的这个子图，是整个有向图中的强连通分量。

解答树：就是一个可以来表达出递归枚举的方式的树（图），其实也可以说是递归图。。反正都是一个作用，一个展示从“什么都没有做”开始到“所有结求出来”逐步完成的过程。“过程！”

神奇海螺结束！！！

tarjan算法，之所以用DFS就是因为它将每一个强连通分量作为搜索树上的一个子树。而这个图，就是一个完整的搜索树。
为了使这颗搜索树在遇到强连通分量的节点的时候能顺利进行。每个点都有两个参数。
1，DFN［］作为这个点搜索的次序编号（时间戳），简单来说就是 第几个被搜索到的。％每个点的时间戳都不一样％。
2，LOW［］作为每个点在这颗树中的，最小的子树的根，每次保证最小，like它的父亲结点的时间戳这种感觉。如果它自己的LOW［］最小，那这个点就应该从新分配，变成这个强连通分量子树的根节点。
ps：每次找到一个新点，这个点LOW［］＝DFN［］。

而为了存储整个强连通分量，这里挑选的容器是，堆栈。每次一个新节点出现，就进站，如果这个点有 出度 就继续往下找。直到找到底，每次返回上来都看一看子节点与这个节点的LOW值，谁小就取谁，保证最小的子树根。如果找到DFN［］＝＝LOW［］就说明这个节点是这个强连通分量的根节点（毕竟这个LOW［］值是这个强连通分量里最小的。）最后找到强连通分量的节点后，就将这个栈里，比此节点后进来的节点全部出栈，它们就组成一个全新的强连通分量。

先来一段伪代码压压惊：

tarjan(u) {

    DFN[u] = Low[u] = ++Index // 为节点u设定次序编号和Low初值

        Stack.push(u)  // 将节点u压入栈中

        for each (u, v) in E // 枚举每一条边

            if (v is not visted) // 如果节点v未被访问过

                tarjan(v) // 继续向下找

                Low[u] = min(Low[u], Low[v])

            else if (v in S) // 如果节点u还在栈内

                Low[u] = min(Low[u], DFN[v])

                if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根

                    repeat v = S.pop  // 将v退栈，为该强连通分量中一个顶点

                    print v

                    until(u == v)

}

首先来一张有向图。网上到处都是这个图。我们就一点一点来模拟整个算法。

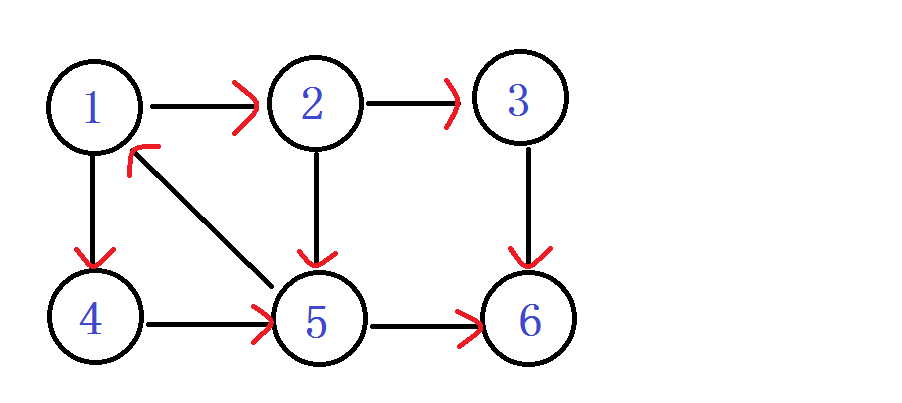
从1进入 DFN［1］＝LOW［1］＝ ＋＋index －－－－1
入栈 1
由1进入2 DFN［2］＝LOW［2］＝ ＋＋index －－－－2
入栈 1 2
之后由2进入3 DFN［3］＝LOW［3］＝ ＋＋index －－－－3
入栈 1 2 3
之后由3进入 6 DFN［6］＝LOW［6］＝＋＋index －－－－4
入栈 1 2 3 6

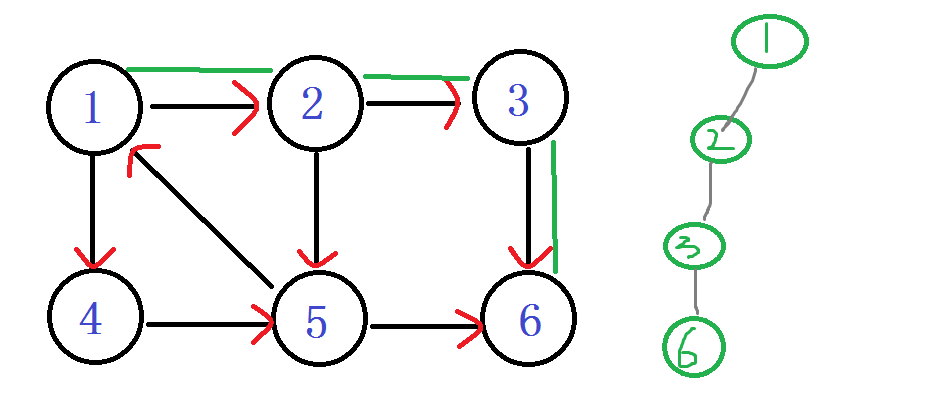
之后发现 嗯？ 6无出度，之后判断 DFN［6］＝＝LOW［6］
说明6是个强连通分量的根节点：6及6以后的点 出栈。
栈： 1 2 3
之后退回 节点3 Low[3] = min(Low[3], Low[6]) LOW［3］还是 3
节点3 也没有再能延伸的边了，判断 DFN［3］＝＝LOW［3］
说明3是个强连通分量的根节点：3及3以后的点 出栈。
栈： 1 2
之后退回 节点2 嗯？！往下到节点5
DFN［5］＝LOW［5］＝ ＋＋index －－－－－5
入栈 1 2 5

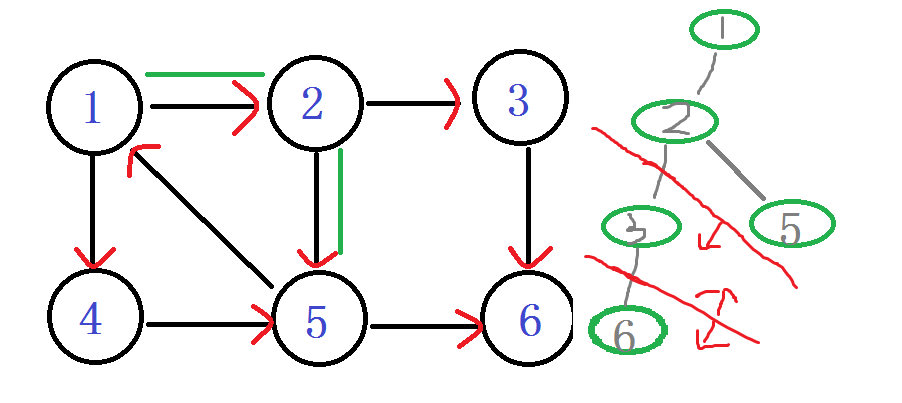
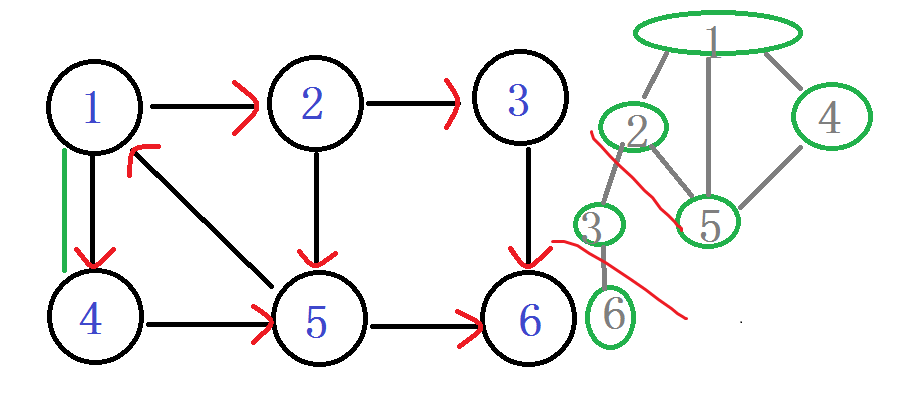
ps：你会发现在有向图旁边的那个丑的（划掉）搜索树 用红线剪掉的子树，那个就是强连通分量子树。每次找到一个。直接。一剪子下去。半个子树就没有了。。

结点5 往下找，发现节点6 DFN［6］有值，被访问过。就不管它。
继续 5往下找，找到了节点1 他爸爸的爸爸。。DFN［1］被访问过并且还在栈中，说明1还在这个强连通分量中，值得发现。 Low[5] = min(Low[5], DFN[1])
确定关系，在这棵强连通分量树中，5节点要比1节点出现的晚。所以5是1的子节点。so
LOW［5］＝ 1

由5继续回到2 Low[2] = min(Low[2], Low[5])
LOW［2］＝1；
由2继续回到1 判断 Low[1] = min(Low[1], Low[2])
LOW［1］还是 1
1还有边没有走过。发现节点4，访问节点4
DFN［4］＝LOW［4］＝＋＋index －－－－6
入栈 1 2 5 4
由节点4，走到5，发现5被访问过了，5还在栈里，
Low[4] = min(Low[4], DFN[5]) LOW［4］＝5
说明4是5的一个子节点。

由4回到1.

回到1，判断 Low[1] = min(Low[1], Low[4])
LOW［1］还是 1 。

判断 LOW［1］ ＝＝ DFN［1］
诶？！相等了 说明以1为根节点的强连通分量已经找完了。
将栈中1以及1之后进栈的所有点，都出栈。
栈 ：（鬼都没有了）

这个时候就完了吗？！

你以为就完了吗？！

然而并没有完，万一你只走了一遍tarjan整个图没有找完怎么办呢？！

所以。tarjan的调用最好在循环里解决。

like 如果这个点没有被访问过，那么就从这个点开始tarjan一遍。

因为这样好让每个点都被访问到。

来一道裸代码。
输入：
一个图有向图。
输出：
它每个强连通分量。

这个图就是刚才讲的那个图。一模一样。

input:

6 8

1 3

1 2

2 4

3 4

3 5

4 6

4 1

5 6

output:

6

5

3 4 2 1

 #include<cstdio>
 #include<algorithm>
 #include<string.h>
 using namespace std;
 struct node {
     int v,next;
 }edge[1001];
  int DFN[1001],LOW[1001];
 int stack[1001],heads[1001],visit[1001],cnt,tot,index;
void add(int x,int y)
{
     edge[++cnt].next=heads[x];
     edge[cnt].v = y;
     heads[x]=cnt;
    return ;
 }
 void tarjan(int x)//代表第几个点在处理。递归的是点。
 {
     DFN[x]=LOW[x]=++tot;// 新进点的初始化。
     stack[++index]=x;//进站
     visit[x]=1;//表示在栈里
    for(int i=heads[x];i!=-1;i=edge[i].next)
     {
         if(!DFN[edge[i].v]) {//如果没访问过
            tarjan(edge[i].v);//往下进行延伸，开始递归
             LOW[x]=min(LOW[x],LOW[edge[i].v]);//递归出来，比较谁是谁的儿子／父亲，就是树的对应关系，涉及到强连通分量子树最小根的事情。
        }
        else if(visit[edge[i].v ]){  //如果访问过，并且还在栈里。
             LOW[x]=min(LOW[x],DFN[edge[i].v]);//比较谁是谁的儿子／父亲。就是链接对应关系
         }
     }
     if(LOW[x]==DFN[x]) //发现是整个强连通分量子树里的最小根。
    {
         do{
            printf("%d ",stack[index]);
             visit[stack[index]]=0;
             index--;
         }while(x!=stack[index+1]);//出栈，并且输出。
         printf("\n");
     }
     return ;
 }
 int main()
 {
     memset(heads,-1,sizeof(heads));
     int n,m;
     scanf("%d%d",&n,&m);
    int x,y;
     for(int i=1;i<=m;i++)
     {
         scanf("%d%d",&x,&y);
        add(x,y);
     }
    for(int i=1;i<=n;i++)
         if(!DFN[i])  tarjan(i);//当这个点没有访问过，就从此点开始。防止图没走完
    return 0;
 }