wqs带权二分
前言
这是一种并不常见的二分方式,通常情况下解决的题目都具有以下明显的特点:
-
求恰好选 \(x\) 次时的最优解
-
我们只会没有次数限制的/加入次数限制后的dp复杂度爆炸 \(\iff\) 只能做没有次数限制的最优解,但是可以知道要选几次(可能比较复杂,之后会解释)
-
随着选择次数的增加,最优解所对应的值增量单调递减/单调递增,形式化的,设 \(f(i)\) 表示当选 \(i\) 次的时候,最优解的值。那么 \(f(i)\) 的图像是一个上凸函数/下凸函数
我们如果能获得凸包,那就好了,但是实际是不能的。
那么有没有别的方法求出凸包上点的值呢?
我们考虑从切线入手,因为凸包上切线的斜率具有单调性
正文
wqs二分通过每次二分一个斜率,找到切点,并根据切线单调性调整斜率,最终找到 \(x\) 对应的斜率
主要解决一下两个问题:
如何找到切点呢,知道 \(x\) 对应的斜率又有什么用呢?
- 先解决第二个问题,因为解决了这个我们才有解决第一个的必要。
改变一下直线方程:
我们的目的是求出 \(f(x)\) ,而知道斜率 \(k\) 后,如果我们可以知道 \(b(x)\) 就可以反解出了。
OK,那么我们可以将求 \(b(x)\) 的任务交给求切点了。
- 求切点
设给定的的斜率为 \(k\) ,切点横坐标为 \(x\),注意这是切线,因此有任意一点 \(x'\) 以 \(k\) 为斜率,都有 \(b_{x'}\) \(\le\) \(b_x\)(如下图)
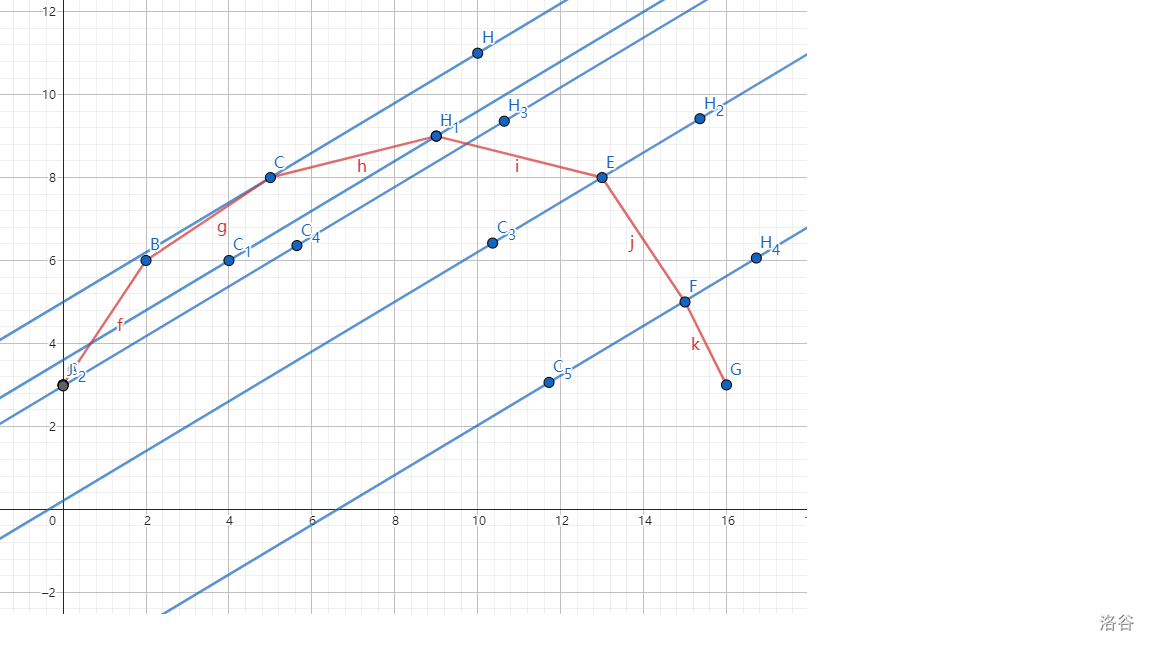
根据:\(b(x)=f(x)-k\times x\)
所有 \(x\) 的 \(b(x)\) 中,\(b_{max}\) 所对应的 \(x'\) 即为切点
此时请回到上面,再次浏览一下特点:“只能做没有次数限制的最优解,但是可以知道要选几次”
我们会的东西可以完美解决这个问题,具体来说:
我们可以给当前每一个选择都减去一个权值 \(k\) ,类似01分数规划,这样就可以使限制消失,进而通过我么可以做到的算法求出 \(b_{max}\) 和其所对应的 \(x'\)
通过求出的 \(x'\) 和实际的 \(x\) 的大小关系,根据斜率单调性,我们可以得出需要调大斜率还是调小斜率。
因此一定可以通过二分找到这个 \(k\).
这里给出伪代码:
int l=?,r=?,ans;
while(l<=r)
{
int mid=l+r>>1;
if(check(mid)>=mid) l=mid+1/r=mid-1,ans=?;
else r=mid-1/l=mid+1;
}
至于是调大二分的值还是调小二分的值,就要看具体是下凸函数(对应求解的是最小值)还是上凸函数(对应求解的是最大值)来看了。
此时可以看模板:P2619 [国家集训队] Tree I
每次二分斜率 \(k\) 后,给每条白边减去一个 \(mid\),然后求一下最小生成树,看一下需要多少条半边,根据这个调整斜率。
但是你认为这样就完了吗,其实还没有,还有问题:
-
有多种属性应该先挑选哪个呢?(白边黑边一样长,先挑哪个?)
-
如果你输出了二分check的cnt(白边的个数),他也不是need呃呃呃。
解决第一个问题
我们需要定义严格偏序规则,也就是说对于两个点,一定要分出先后。
可以感性的思考一下:我们的算法中在不改变求出的是最优解的情况下,是更倾向于选择一次限制,还是选择一个非限制。以上一题为例:就是不改变最小生成树大小的前提下,是优先选白边,还是优先选黑边。
-
如果更倾向于选限制:那么我们只会存凸包同一条直线上最靠右的点
-
如果更倾向于不选限制:那么我们只会存凸包同一条直线上最靠左的点
以此图为例可能更好理解。
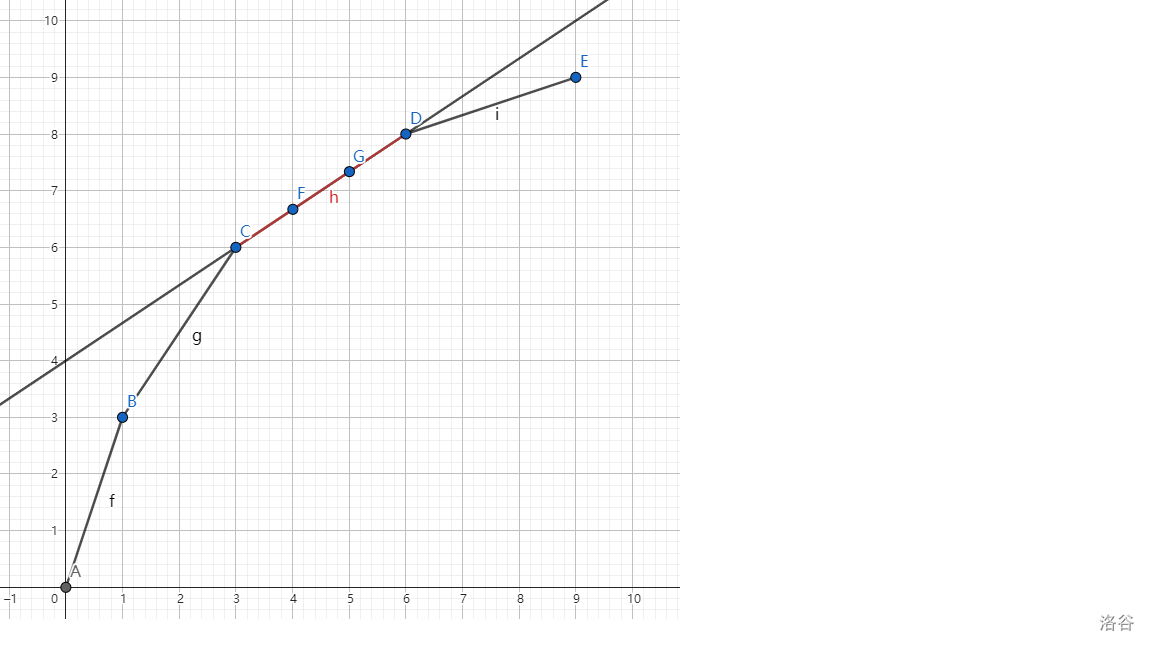
如果是第一种,我们在check的时候就要在 \(cnt \ge need\) 的时候统计答案。
如果是第二种,我们在check的时候就要在 \(cnt \le need\) 的时候统计答案
上面两个结论在代码实现上非常重要。
解决第二个问题:
有了第一个的铺垫,第二个就好说了,为什么求出的切点一直不是need呢?
继续看此图:
\(C,F,G,D\) 四个点都是当前斜率下的切点,转化为更直白一点的说法就是,当前 \(b_{max}\) 所对应的 \(x'\) 不唯一。
而在这些点中,我们永远只会存一个,因为我们定义了严格偏序规则,我们一定会挑一个端点存,这就是我们无论如何改变斜率,都凑不出来 \(need\) 的原因。
因此在计算答案的时候,我们应该使 \(ans=size+mid\times k\)
,而不能直接用二分出来的 \(cnt\) 来算最终的答案。
原因是我们的 \(x\) 可能是 \(F,D\)这一类不在端点上的,和二分出来的cnt的关系仅仅是他们的斜率相同,而不是纵坐标也就是对应的 \(f(i)\) 相同。
上代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct Edge
{
int a,b,w;
int c;
bool operator<(const Edge &t)const
{
if(w==t.w) return c<t.c;
return w<t.w;
}
}e[N];
int p[N];
int n,m,need;
int sum;
void init()
{
for(int i=1;i<=n;i++) p[i]=i;
sum=0;
}
int find(int x)
{
if(x!=p[x]) return p[x]=find(p[x]);
return p[x];
}
int kruskal(int mid)
{
for(int i=1;i<=m;i++) if(!e[i].c) e[i].w-=mid;
sort(e+1,e+1+m);
init();
int cnt=0;
for(int i=1;i<=m;i++)
{
int pa=find(e[i].a),pb=find(e[i].b);
if(pa==pb) continue;
p[pa]=pb;
sum+=e[i].w;
cnt+=(!e[i].c);
}
for(int i=1;i<=m;i++) if(!e[i].c) e[i].w+=mid;
return cnt;
}
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>m>>need;
for(int i=1,a,b,w,c;i<=m;i++)
{
cin>>a>>b>>w>>c;
a++,b++;
e[i]={a,b,w,c};
}
int l=-111,r=111,ans;
while(l<=r)
{
int mid=l+r>>1;
if(kruskal(mid)>=need) r=mid-1,ans=sum+need*mid;
else l=mid+1;
}
cout<<ans<<"\n";
}
总结
wqs二分是比较套路的,但是需要思考全面,主要是三个细节
-
确定 \(f(i)\) 是一个凸函数或凹函数,主要取决于限制和求解的问题
-
定义好偏序规则,确定当 \(b\) 相同的时候我们是选左端点还是右端点。
-
确定好二分范围
这里主要补充一下第三点,因为我们的斜率是单调的,因此要确定上下界并不难,只需要考虑从 \(0->1\) 的答案增量和从 \(x-1->x\) 的答案增量即可。或从定义入手,多选一个点带来的最大变化量是多少
比如上一题中就是:改变一条边最多会产生 \(max_{e_w}\) 的贡献。或者,当添加第一条白边的时候,一定会去掉路径上最大的黑边,因此最大变化量为 \(max_{e_w}\)
例题(待补充)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号