HDU 6333:Harvest of Apples
Problem B. Harvest of Apples
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 347 Accepted Submission(s): 121
Problem Description
There are $n$ apples on a tree, numbered from $1$ to $n$.
Count the number of ways to pick at most $m$ apples.
Count the number of ways to pick at most $m$ apples.
Input
The first line of the input contains an integer $T$ $(1 \le T \le 10 ^ 5)$ denoting the number of test cases.
Each test case consists of one line with two integers $n, m$ $(1 \le m \le n \le 10 ^ 5)$.
Each test case consists of one line with two integers $n, m$ $(1 \le m \le n \le 10 ^ 5)$.
Output
For each test case, print an integer representing the number of ways modulo $10 ^ 9 + 7$.
Sample Input
2
5 2
1000 500
Sample Output
16
924129523
Source
Recommend
chendu
分析:这题显然暴力O(n^2)是要TLE的,比赛的时候考虑简单数学优化一下变成2.5e9,显然肯定也是要TLE的。后来考虑深度数学优化得出:
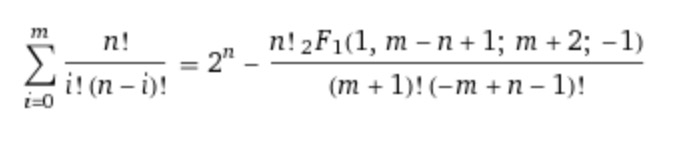
其中F1表示超几何函数。。。然而找了半个多小时没有找到C++的模板。。就很绝望
补题的时候发现可以用莫队和分块去搞,学了半天嘤嘤嘤,太菜了。

#include <iostream> #include <string> #include <cstdio> #include <cmath> #include <cstring> #include <algorithm> #include <vector> #include <queue> #include <deque> #include <stack> #include <map> #define LL long long #define elif else if #define range(i,a,b) for(auto i=a;i<=b;++i) #define rerange(i,a,b) for(auto i=a;i>=b;--i) #define itrange(i,a,b) for(auto i=a;i!=b;++i) #define fill(arr,tmp) memset(arr,tmp,sizeof(arr)) using namespace std; int t,n,m,block[int(2e5)],interval,id=1; struct query{ int n,k,i; }Q[int(1e5+5)]; vector<query>ll[int(1e5+5)]; bool cmp(query a,query b){ return a.n<b.n; } const int mod=int(1e9+7); LL fac[int(1e5+5)],inv[int(1e5+5)],ans[int(1e5+5)]; LL q_pow(LL a,LL b){ if(b<0)return 0; LL ret=1; a%=mod; while(b){ ret=b&1?ret*a%mod:ret; b>>=1; a=a*a%mod; } return ret; } LL C(LL n,LL m){ if(n<m)return 0; return fac[n]*inv[m]%mod*inv[n-m]%mod; } void init(){ fac[0]=1; range(i,1,int(1e5))fac[i]=fac[i-1]*i%mod; inv[int(1e5)]=q_pow(fac[int(1e5)],mod-2); rerange(i,int(1e5-1),0)inv[i]=inv[i+1]*(i+1)%mod; interval=int(sqrt(1e5)); for(int i=1;i<=int(1e5);i+=interval,++id) for(int j=i;j<i+interval and j<=int(1e5);++j)block[j]=id; --id; scanf("%d",&t); range(i,1,t){ scanf("%d%d",&(Q+i)->n,&(Q+i)->k); (Q+i)->i=i; ll[block[Q[i].k]].push_back(Q[i]); } } void solve(){ range(i,1,id) if(ll[i].size()){ sort(ll[i].begin(),ll[i].end(),cmp); LL val=0,in=ll[i][0].n,ik=-1; range(j,0,ll[i].size()-1){ while(in<ll[i][j].n)val=((val<<1)+mod-C(in++,ik))%mod; while(ik<ll[i][j].k)val=(val+C(in,++ik))%mod; while(ik>ll[i][j].k)val=(val+mod-C(in,ik--))%mod; ans[ll[i][j].i]=val; } } range(i,1,t)printf("%lld\n",ans[i]); } int main() { init(); solve(); return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号