BZOJ3295[CQOI2011]动态逆序对（CDQ分治）
第一个不看题解A了的CDQ题目QwQ
Time Limit: 10 Sec Memory Limit: 128 MB
Description
对于序列A，它的逆序对数定义为满足i<j，且Ai>Aj的数对(i,j)的个数。给1到n的一个排列，按照某种顺序依次删
除m个元素，你的任务是在每次删除一个元素之前统计整个序列的逆序对数
Input
输入第一行包含两个整数n和m，即初始元素的个数和删除的元素个数。
以下n行每行包含一个1到n之间的正整数，即初始排列。
以下m行每行一个正整数，依次为每次删除的元素。
N<=100000 M<=50000
Output
输出包含m行，依次为删除每个元素之前，逆序对的个数。
Sample Input
5 4
1
5
3
4
2
5
1
4
2
Sample Output
5
2
2
1
样例解释
(1,5,3,4,2)(1,3,4,2)(3,4,2)(3,2)(3)。
解析：
1.逆序对个数是满足a[i]>a[j]&&i<j的(i, j)个数。
2.题目说删除，不好处理，我们倒过来当成添加元素，统计每次添加元素会增加多少个逆序对，答案为依次累加的和。
3.一个操作除了可以用顺序（也可理解为时间）和位置表示，为了方便还可扩展为顺序（时间）、位置、数值三个指标表示，那么对于（pos[i]，a[i]，time[i])，增加的逆序对个数等于满足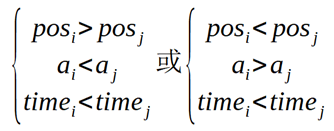
的j的个数（注意time的大小关系，因为是倒过来，时间大的先添加）。
4.没有删完的情况，剩下的部分人为地随便顺序删掉就行，补齐n个操作。
5.答案会爆int。
然后就可以先对time排序，分两半，右边加进树状数组，更新左边的答案，再递归处理两半。
我的代码很乱很乱很乱
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 using namespace std; 6 7 struct Query 8 { 9 int id, pos, val; 10 }q[100010], tmp[100010]; 11 12 int n, m, cnt, pos[100010], arr[100010], tree[100010]; 13 long long ans[100010]; 14 15 void Add(int, int); 16 int query(int); 17 void CDQ(int, int); 18 bool cmp(Query, Query); 19 20 int main() 21 { 22 scanf("%d%d", &n, &m); 23 for(int i = 0; i < n; i++) 24 { 25 scanf("%d", arr + i); 26 pos[arr[i]] = i; 27 } 28 for(cnt = 0; cnt < m; cnt++) 29 { 30 int t; 31 scanf("%d", &t); 32 q[cnt].pos = pos[t]; 33 q[cnt].val = t; 34 q[cnt].id = cnt; 35 arr[pos[t]] = 0; 36 } 37 for(int i = 0; i < n; i++) 38 if(arr[i]) 39 { 40 q[cnt].pos = i; 41 q[cnt].val = arr[i]; 42 q[cnt].id = cnt; 43 cnt++; 44 } 45 sort(q, q + n); 46 CDQ(0, n - 1); 47 for(int i = n - 1; i >= 0; i--) 48 ans[i] += ans[i + 1]; 49 for(int i = 0; i < m; i++) 50 printf("%lld\n", ans[i]); 51 52 return 0; 53 } 54 void Add(int _pos, int val) 55 { 56 for(int i = _pos; i <= n; i += (i & (-i))) 57 tree[i] += val; 58 } 59 60 int query(int _pos) 61 { 62 int res = 0; 63 for(int i = _pos; i > 0; i -= (i & (-i))) 64 res += tree[i]; 65 return res; 66 } 67 68 bool operator <(Query a, Query b) 69 { 70 return a.pos < b.pos; 71 } 72 73 void CDQ(int l, int r) 74 { 75 if(l == r) return; 76 int mid = (l + r) >> 1; 77 for(int i = l; i <= r; i++) 78 if(q[i].id <= mid) ans[q[i].id] += (long long)query(n) - query(q[i].val); 79 else Add(q[i].val, 1); 80 for(int i = l; i <= r; i++) 81 if(q[i].id > mid) 82 Add(q[i].val, -1); 83 for(int i = r; i >= l; i--) 84 if(q[i].id <= mid) ans[q[i].id] += (long long)query(q[i].val); 85 else Add(q[i].val, 1); 86 for(int i = l; i <= r; i++) 87 if(q[i].id > mid) 88 Add(q[i].val, -1); 89 int l1 = l, l2 = mid + 1; 90 for(int i = l; i <= r; i++) 91 if(q[i].id <= mid) tmp[l1++] = q[i]; 92 else tmp[l2++] = q[i]; 93 for(int i = l; i <= r; i++) 94 q[i] = tmp[i]; 95 CDQ(l, mid); 96 CDQ(mid + 1, r); 97 } 98 //Rhein_E
这是一个悲伤的故事。。。。
