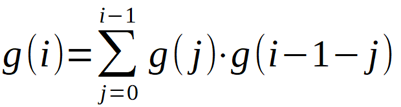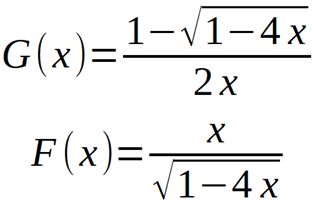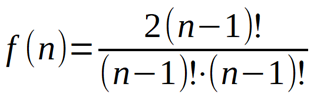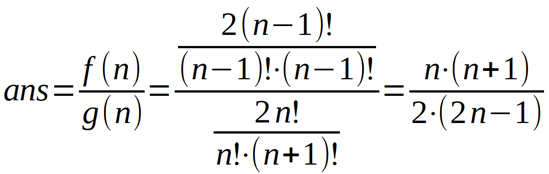BZOJ4001[TJOI2015]概率论（数学、期望、生成函数、卡特兰数）
题目传送：https://www.lydsy.com/JudgeOnline/problem.php?id=4001
Description
.png)
Input
输入一个正整数N，代表有根树的结点数
Output
输出这棵树期望的叶子节点数。要求误差小于1e-9
Sample Input
1
Sample Output
1.000000000
HINT
1<=N<=10^9
既然每种形态出现的概率相同，如果g(i)表示有i个节点的二叉树形态数，f(i)表示有i个节点的二叉树所有形态的叶子节点个数之和，那么答案显然是f(n)/g(n)。考虑计算g(i)，除去一个节点作为根，其余的节点分到左右子树，不难得出递推式：
计算f(i),枚举左子树，累加左子树的贡献，右子树等价，不难得出递推式：
观察这两个式子，都是卷积的形式，卷积对应着生成函数相乘，那么构造f(x)的生成函数F(x)，g(x)的生成函数G(x)，根据递推式可得：
解得：
G(x)不取另一根是为了让函数收敛。
利用广义二项式定理展开，一波推导可得：
那么：
我只想说：打表找规律多好啊！！！
代码：
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 using namespace std; 5 6 int main() 7 { 8 double n; 9 scanf("%lf" , &n); 10 printf("%.9lf\n" , n * (n + 1) / (2 * n - 1) / 2); 11 return 0; 12 }//Rhein_E
